Python での主成分回帰 (ステップバイステップ)

p個の予測子変数のセットと応答変数が与えられると、多重線形回帰では最小二乗法として知られる方法を使用して残差二乗和 (RSS) を最小化します。

RSS = Σ(y _i – ŷ _i ) ²

金：

• Σ : 和を意味するギリシャ語の記号
• y _i : ^{i 番目の}観測値の実際の応答値
• ŷ _i : 重回帰モデルに基づく予測応答値

ただし、予測変数の相関性が高い場合、 多重共線性が問題になる可能性があります。これにより、モデルの係数推定の信頼性が低くなり、大きな分散が示される可能性があります。

この問題を回避する 1 つの方法は、主成分回帰を使用することです。これは、元のp個の予測子のM 個の線形結合 (「主成分」と呼ばれます) を見つけ、最小二乗を使用して、主成分を予測子として使用して線形回帰モデルを近似します。

このチュートリアルでは、Python で主成分回帰を実行する方法のステップバイステップの例を提供します。

ステップ 1: 必要なパッケージをインポートする

まず、Python で主成分回帰 (PCR) を実行するために必要なパッケージをインポートします。

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn. PCA import decomposition
from sklearn. linear_model import LinearRegression
from sklearn. metrics import mean_squared_error

ステップ 2: データをロードする

この例では、33 台の異なる車に関する情報が含まれるmtcarsというデータセットを使用します。応答変数としてhp を使用し、予測変数として次の変数を使用します。

• mpg
• 画面
• たわごと
• 重さ
• qsec

次のコードは、このデータセットをロードして表示する方法を示しています。

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

ステップ 3: PCR モデルを調整する

次のコードは、PCR モデルをこのデータに適合させる方法を示しています。次の点に注意してください。

• pca.fit_transform(scale(X)) : これは、各予測子変数が平均 0、標準偏差 1 になるようにスケーリングする必要があることを Python に指示します。これが起こります。さまざまな単位で測定されます。
• cv = RepeatedKFold() : これは、モデルのパフォーマンスを評価するためにk 分割相互検証を使用するように Python に指示します。この例では、k = 10 の折りを選択し、3 回繰り返します。

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#scale predictor variables
pca = pca()
X_reduced = pca. fit_transform ( scale (X))

#define cross validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

regr = LinearRegression()
mse = []

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (regr,
           n.p. ones ((len(X_reduced),1)), y, cv=cv,
           scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    score = -1*model_selection. cross_val_score (regr,
               X_reduced[:,:i], y, cv=cv, scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)
    
# Plot cross-validation results    
plt. plot (mse)
plt. xlabel ('Number of Principal Components')
plt. ylabel ('MSE')
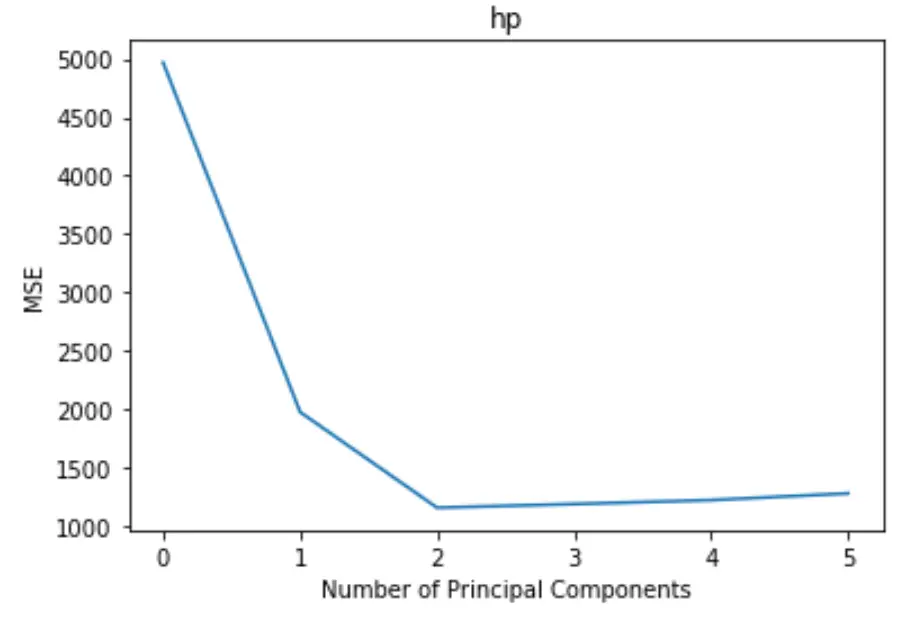
plt. title ('hp') 

プロットでは、X 軸に主成分の数が表示され、Y 軸に MSE (平均二乗誤差) 検定が表示されます。

グラフから、2 つの主成分を追加するとテストの MSE が減少しますが、3 つ以上の主成分を追加すると増加し始めることがわかります。

したがって、最適なモデルには最初の 2 つの主成分のみが含まれます。

次のコードを使用して、各主成分をモデルに追加することで説明される応答変数の分散のパーセンテージを計算することもできます。

 n.p. cumsum (np. round (pca. explained_variance_ratio_ , decimals= 4 )* 100 )

array([69.83, 89.35, 95.88, 98.95, 99.99])

次のことがわかります。

• 最初の主成分のみを使用すると、応答変数の変動の69.83%を説明できます。
• 第 2 主成分を追加することで、応答変数の変動の89.35%を説明できます。

より多くの主成分を使用することでより多くの分散を説明できることに注意してください。ただし、2 つ以上の主成分を追加しても、実際には説明される分散のパーセンテージはそれほど増加しないことがわかります。

ステップ 4: 最終モデルを使用して予測を行う

最終的な 2 主成分 PCR モデルを使用して、新しい観測値についての予測を行うことができます。

次のコードは、元のデータセットをトレーニング セットとテスト セットに分割し、2 つの主成分を持つ PCR モデルを使用してテスト セットで予測を行う方法を示しています。

 #split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size= 0.3 , random_state= 0 ) 

#scale the training and testing data
X_reduced_train = pca. fit_transform ( scale (X_train))
X_reduced_test = pca. transform ( scale (X_test))[:,:1]

#train PCR model on training data 
regr = LinearRegression()
reg. fit (X_reduced_train[:,:1], y_train)

#calculate RMSE
pred = regr. predict (X_reduced_test)
n.p. sqrt ( mean_squared_error (y_test, pred))

40.2096

RMSE テストの結果が40.2096であることがわかります。これは、テスト セットの観測値の予測hp値と観測されたhp値の間の平均偏差です。

この例で使用されている完全な Python コードは、 ここにあります。