Python で分位点回帰を実行する方法

線形回帰は、1 つ以上の予測変数と応答変数の間の関係を理解するために使用できる方法です。

通常、線形回帰を実行するときは、応答変数の平均値を推定する必要があります。

ただし、代わりに分位点回帰として知られる方法を使用して、70 パーセンタイル、90 パーセンタイル、98 パーセンタイルなどの応答値の任意の分位値またはパーセンタイル値を推定することもできます。

このチュートリアルでは、この関数を使用して Python で分位点回帰を実行する方法の段階的な例を示します。

ステップ 1: 必要なパッケージをロードする

まず、必要なパッケージと関数をロードします。

 import numpy as np
import pandas as pd
import statsmodels. api as sm
import statsmodels. formula . api as smf
import matplotlib. pyplot as plt

ステップ 2: データを作成する

この例では、大学の 100 人の学生の学習時間と得られた試験結果を含むデータセットを作成します。

 #make this example reproducible
n.p. random . seeds (0)

#create dataset
obs = 100

hours = np. random . uniform (1, 10, obs)
score = 60 + 2*hours + np. random . normal (loc=0, scale=.45*hours, size=100)

df = pd. DataFrame ({' hours ':hours, ' score ':score})

#view first five rows
df. head ()

hours score
0 5.939322 68.764553
1 7.436704 77.888040
2 6.424870 74.196060
3 5.903949 67.726441
4 4.812893 72.849046

ステップ 3: 分位点回帰を実行する

次に、学習時間を予測変数として、試験のスコアを応答変数として使用して、分位点回帰モデルを近似します。

このモデルを使用して、学習時間数に基づいて試験スコアの予想される 90 パーセンタイルを予測します。

 #fit the model
model = smf. quantreg ('score~hours', df). fit (q= 0.9 )

#view model summary
print ( model.summary ())

                         QuantReg Regression Results                          
==================================================== ============================
Dept. Variable: Pseudo R-squared score: 0.6057
Model: QuantReg Bandwidth: 3.822
Method: Least Squares Sparsity: 10.85
Date: Tue, 29 Dec 2020 No. Observations: 100
Time: 15:41:44 Df Residuals: 98
                                        Model: 1
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
Intercept 59.6104 0.748 79.702 0.000 58.126 61.095
hours 2.8495 0.128 22.303 0.000 2.596 3.103
==================================================== ============================

結果から、推定された回帰式がわかります。

試験スコアの 90 パーセンタイル = 59.6104 + 2.8495*(時間)

たとえば、8 時間勉強した生徒全員の 90 パーセンタイル スコアは 82.4 になるはずです。

試験スコアの 90 パーセンタイル = 59.6104 + 2.8495*(8) = 82.4 。

出力には、予測子変数の切片と時間の信頼限界の上限と下限も表示されます。

ステップ 4: 結果を視覚化する

近似された分位点回帰式をグラフに重ねた散布図を作成して、回帰結果を視覚化することもできます。

 #define figure and axis
fig, ax = plt.subplots(figsize=(8, 6))

#get y values
get_y = lambda a, b: a + b * hours
y = get_y( model.params [' Intercept '], model.params [' hours '])

#plot data points with quantile regression equation overlaid
ax. plot (hours, y, color=' black ')
ax. scatter (hours, score, alpha=.3)
ax. set_xlabel (' Hours Studied ', fontsize=14)
ax. set_ylabel (' Exam Score ', fontsize=14)

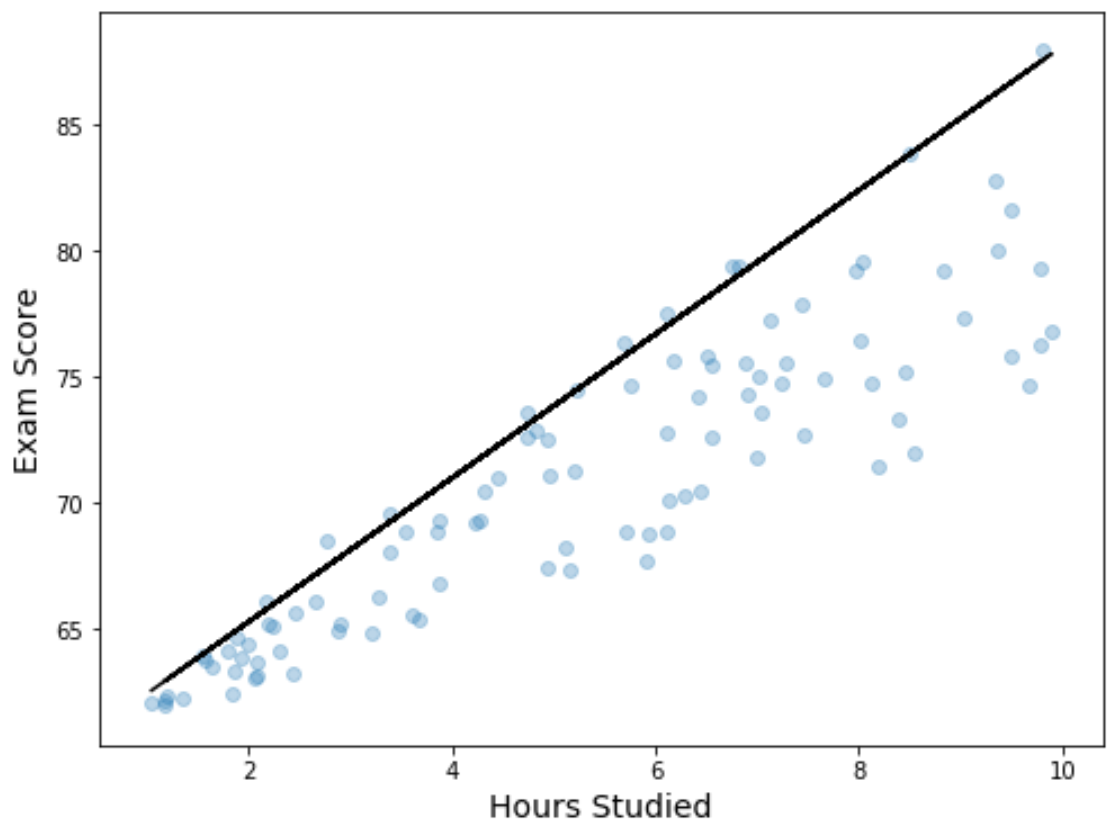
単純な線形回帰直線とは異なり、この近似直線はデータの「最適な近似直線」を表すものではないことに注意してください。代わりに、予測子変数の各レベルで推定された 90 パーセンタイルを通過します。

追加リソース

Python で単純な線形回帰を実行する方法
Python で二次回帰を実行する方法