Python の部分最小二乗法 (ステップバイステップ)

機械学習で遭遇する最も一般的な問題の 1 つは、 多重共線性です。これは、データセット内の 2 つ以上の予測子変数の相関性が高い場合に発生します。

これが起こると、モデルはトレーニング データ セットにうまく適合できるかもしれませんが、トレーニング データ セットに過剰適合するため、これまでに見たことのない新しいデータ セットではパフォーマンスが低下する可能性があります。トレーニングセット。

この問題を回避する 1 つの方法は、次のように機能する 部分最小二乗法と呼ばれる方法を使用することです。

• 予測変数と応答変数を標準化します。
• 応答変数と予測子変数の両方における有意な量の変動を説明する、 p個の元の予測子変数のM 個の線形結合 (「PLS 成分」と呼ばれる) を計算します。
• 最小二乗法を使用して、PLS コンポーネントを予測子として使用して線形回帰モデルを近似します。
• k 分割交差検証を使用して、モデルに保持する PLS コンポーネントの最適な数を見つけます。

このチュートリアルでは、Python で部分最小二乗法を実行する方法を段階的に説明します。

ステップ 1: 必要なパッケージをインポートする

まず、Python で部分最小二乗法を実行するために必要なパッケージをインポートします。

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

ステップ 2: データをロードする

この例では、33 台の異なる車に関する情報が含まれるmtcarsというデータセットを使用します。応答変数としてhp を使用し、予測変数として次の変数を使用します。

• mpg
• 画面
• たわごと
• 重さ
• qsec

次のコードは、このデータセットをロードして表示する方法を示しています。

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

ステップ 3: 部分最小二乗モデルを当てはめる

次のコードは、PLS モデルをこのデータに適合させる方法を示しています。

cv =repeatedKFold() は、k 分割相互検証を使用してモデルのパフォーマンスを評価するように Python に指示することに注意してください。この例では、k = 10 の折りを選択し、3 回繰り返します。

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

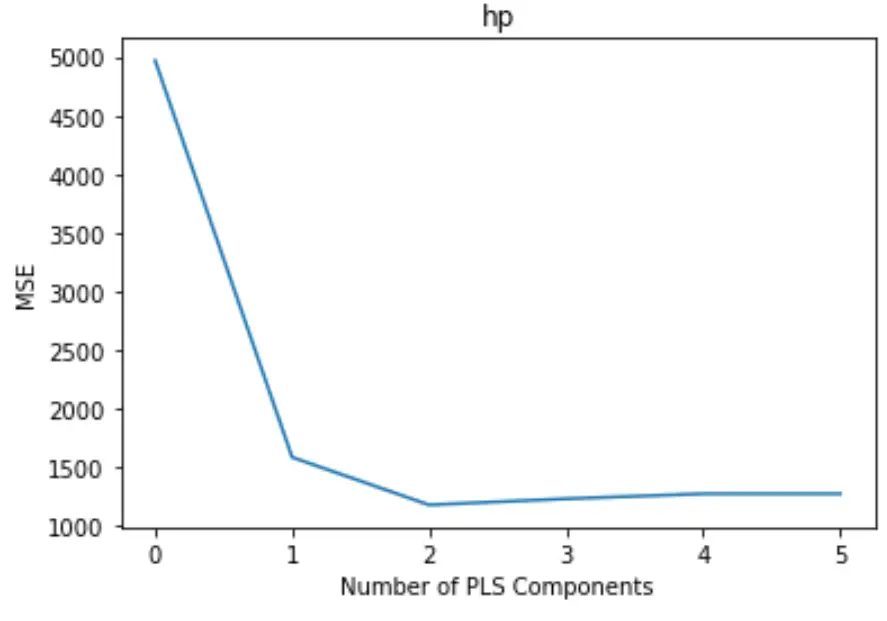
プロットでは、X 軸に沿って PLS コンポーネントの数が表示され、Y 軸に沿って MSE (平均二乗誤差) テストが表示されます。

グラフから、2 つの PLS コンポーネントを追加するとテストの MSE が減少しますが、3 つ以上の PLS コンポーネントを追加すると増加し始めることがわかります。

したがって、最適なモデルには最初の 2 つの PLS コンポーネントのみが含まれます。

ステップ 4: 最終モデルを使用して予測を行う

2 つの PLS コンポーネントを含む最終的な PLS モデルを使用して、新しい観測値についての予測を行うことができます。

次のコードは、元のデータ セットをトレーニング セットとテスト セットに分割し、2 つの PLS コンポーネントを含む PLS モデルを使用してテスト セットで予測を行う方法を示しています。

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

テストの RMSE が29.9094であることがわかります。これは、テスト セットの観測値の予測hp値と観測されたhp値の間の平均偏差です。

この例で使用されている完全な Python コードは、 ここにあります。