Python で残差プロットを作成する方法

残差プロットは、回帰モデルの残差に対する近似値を表示するプロットの一種です。

このタイプのプロットは、線形回帰モデルが特定のデータセットに適切かどうかを評価し、残差の不均一分散性をチェックするためによく使用されます。

このチュートリアルでは、Python で線形回帰モデルの残差プロットを作成する方法を説明します。

例: Python の残差プロット

この例では、10 人のバスケットボール選手の属性を記述するデータセットを使用します。

 import numpy as np
import pandas as pd

#create dataset
df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86],
                   'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19],
                   'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5],
                   'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]})

#view dataset
df

	rating points assists rebounds
0 90 25 5 11
1 85 20 7 8
2 82 14 7 10
3 88 16 8 6
4 94 27 5 6
5 90 20 7 9
6 76 12 6 6
7 75 15 9 10
8 87 14 9 10
9 86 19 5 7

単純線形回帰の残差プロット

予測変数としてポイントを使用し、応答変数としてグレードを使用して単純な線形回帰モデルを近似するとします。

 #import necessary libraries
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols

#fit simple linear regression model
model = ols('rating ~ points', data=df). fit ()

#view model summary
print(model.summary())

statsmodels ライブラリのLot_regress_exog() 関数を使用して、残差プロットまたは近似プロットを作成できます。

 #define figure size
fig = plt.figure(figsize=(12,8))

#produce regression plots
fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)

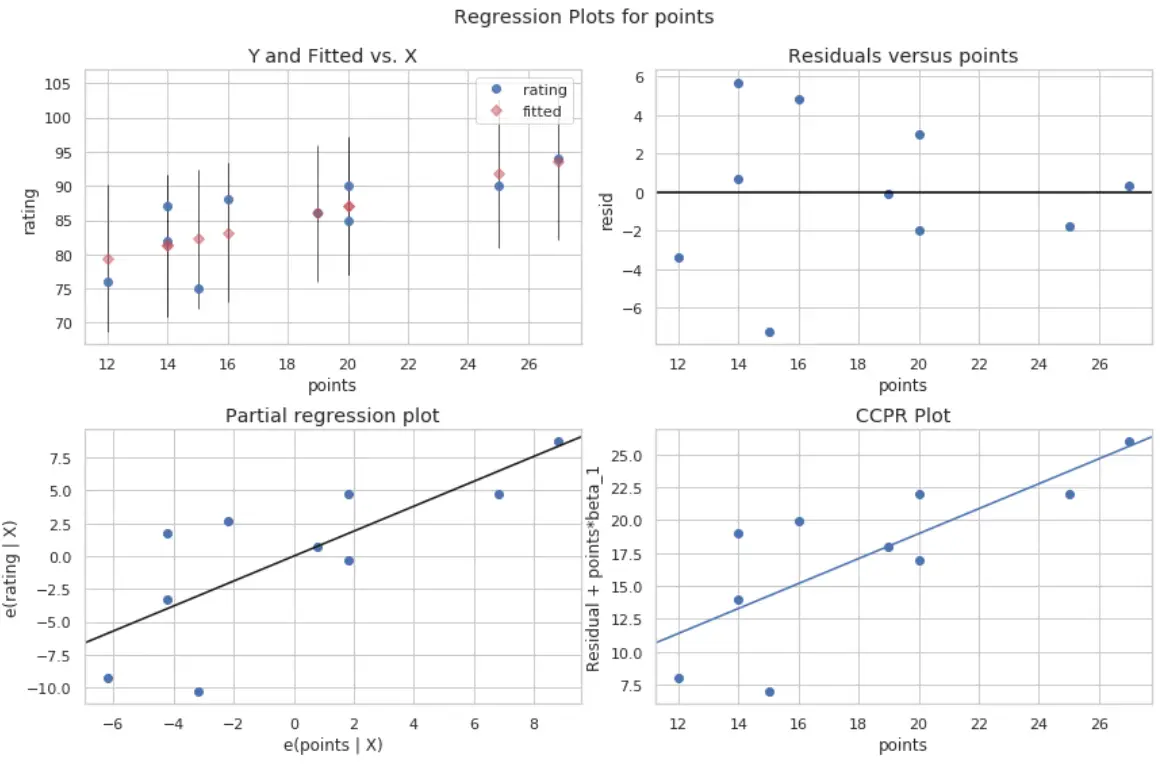
4 つのプロットが作成されます。右上隅にあるのは、残差プロットと調整済みプロットです。このプロットの X 軸は予測変数点の実際の値を示し、Y 軸はその値の残差を示します。

残差はゼロの周囲にランダムに分散しているように見えるため、これは、予測子変数の不均一分散性が問題ではないことを示しています。

重回帰の残差プロット

代わりに、予測変数としてアシストとリバウンドを使用し、応答変数として評価を使用して重線形回帰モデルを近似するとします。

 #fit multiple linear regression model
model = ols('rating ~ assists + rebounds', data=df). fit ()

#view model summary
print(model.summary())

もう一度、statsmodels ライブラリのLot_regress_exog() 関数を使用して、個々の予測子のそれぞれについて残差対予測子のプロットを作成できます。

たとえば、予測子変数アシストの残差/予測子プロットは次のようになります。

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)

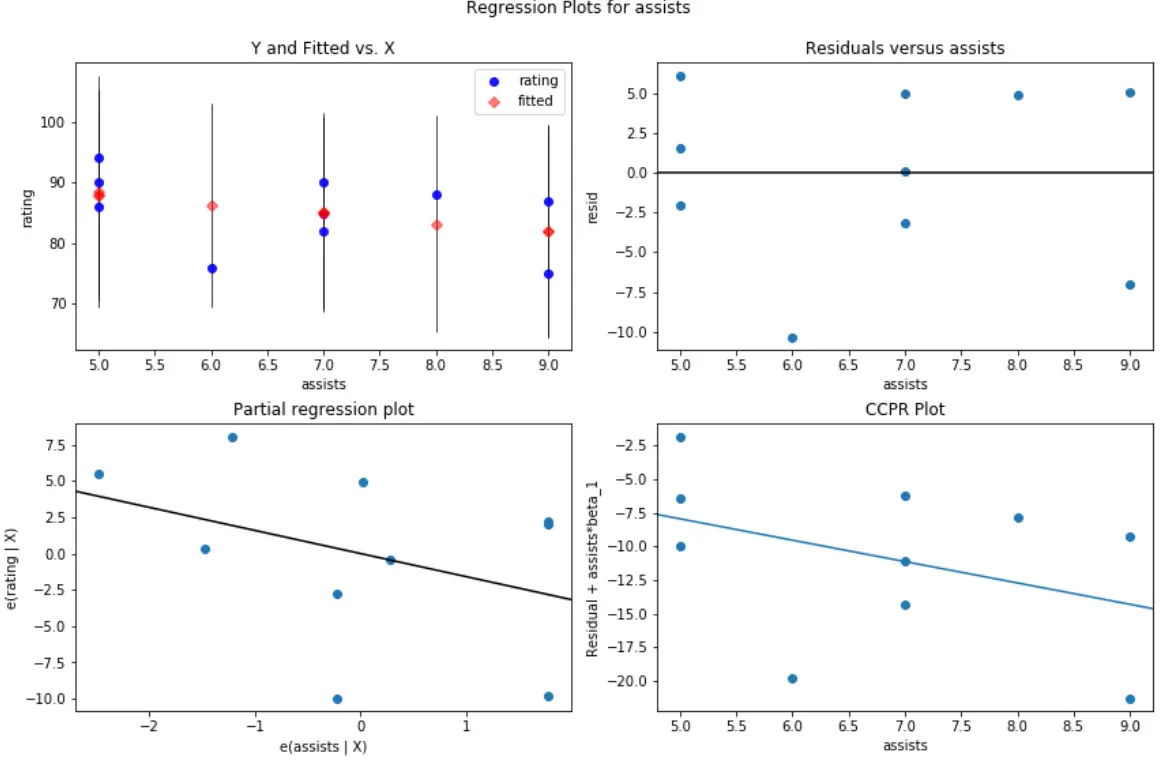
そして、これは、予測子変数bouncesの残差/予測子プロットがどのように見えるかです。

 #create residual vs. predictor plot for 'assists'
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)

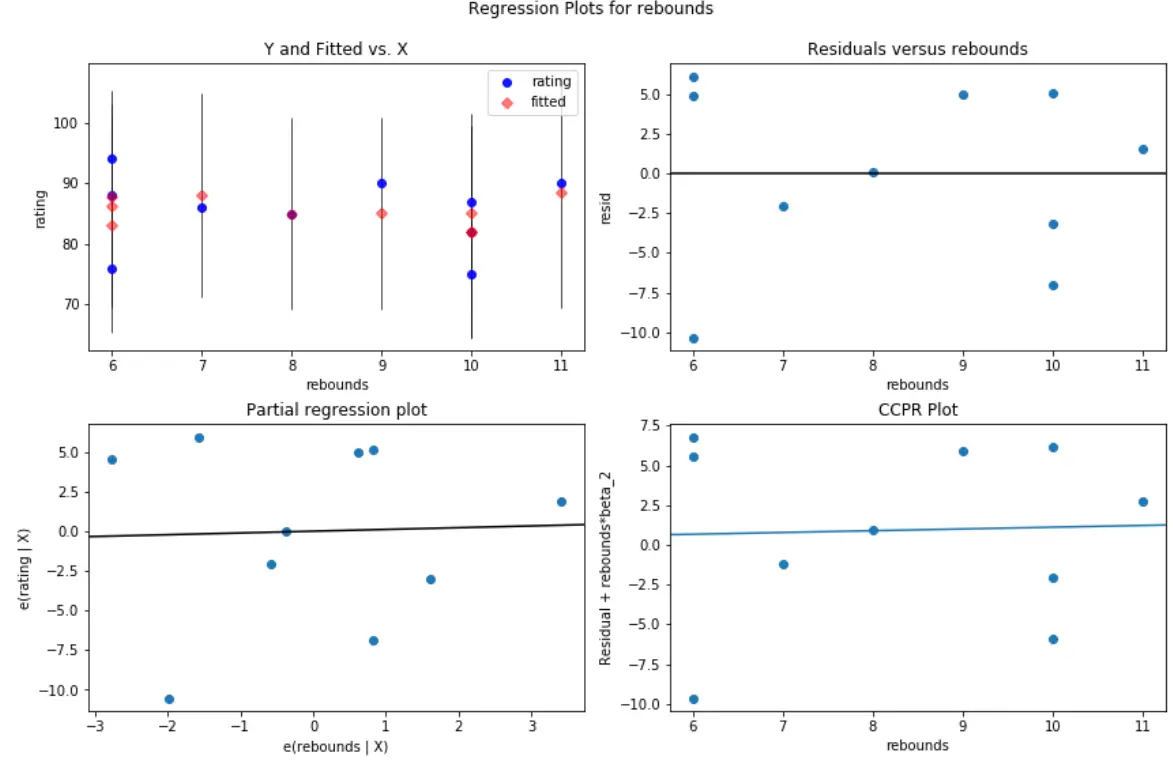
どちらのプロットでも、残差はゼロの周りにランダムに分散しているように見えます。これは、モデル内のどの予測変数にも不均一分散性が問題ではないことを示しています。