R での曲線近似 (例付き)
多くの場合、R の曲線に最もよく適合する方程式を見つけたい場合があります。

次のステップバイステップの例では、 poly()関数を使用して曲線を R のデータに適合させる方法と、どの曲線がデータに最も適合するかを判断する方法を説明します。
ステップ 1: データの作成と視覚化
まず偽のデータセットを作成し、次に散布図を作成してデータを視覚化しましょう。
#create data frame df <- data. frame (x=1:15, y=c(3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46)) #create a scatterplot of x vs. y plot(df$x, df$y, pch= 19 , xlab=' x ', ylab=' y ')
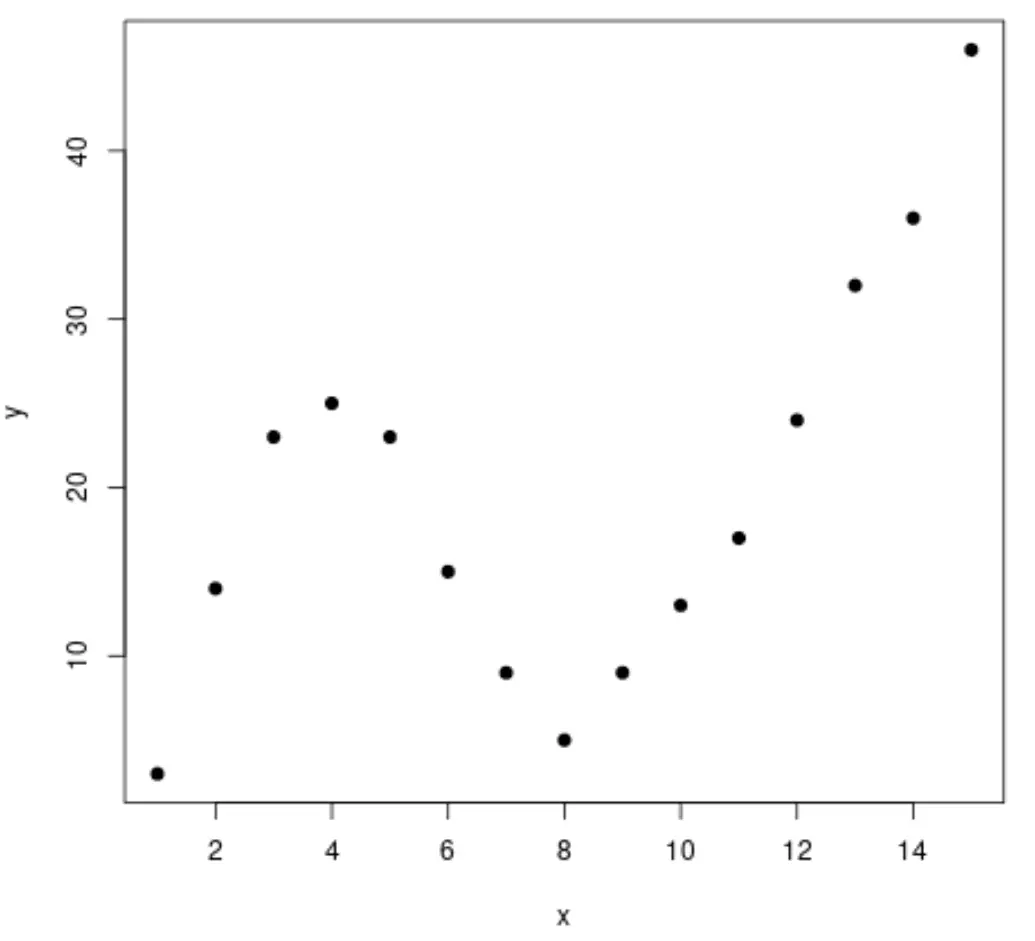
ステップ 2: 複数のカーブを調整する
次に、いくつかの多項式回帰モデルをデータに適合させ、同じプロットで各モデルの曲線を視覚化してみましょう。
#fit polynomial regression models up to degree 5 fit1 <- lm(y~x, data=df) fit2 <- lm(y~poly(x,2,raw= TRUE ), data=df) fit3 <- lm(y~poly(x,3,raw= TRUE ), data=df) fit4 <- lm(y~poly(x,4,raw= TRUE ), data=df) fit5 <- lm(y~poly(x,5,raw= TRUE ), data=df) #create a scatterplot of x vs. y plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ') #define x-axis values x_axis <- seq(1, 15, length= 15 ) #add curve of each model to plot lines(x_axis, predict(fit1, data. frame (x=x_axis)), col=' green ') lines(x_axis, predict(fit2, data. frame (x=x_axis)), col=' red ') lines(x_axis, predict(fit3, data. frame (x=x_axis)), col=' purple ') lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ') lines(x_axis, predict(fit5, data. frame (x=x_axis)), col=' orange ')
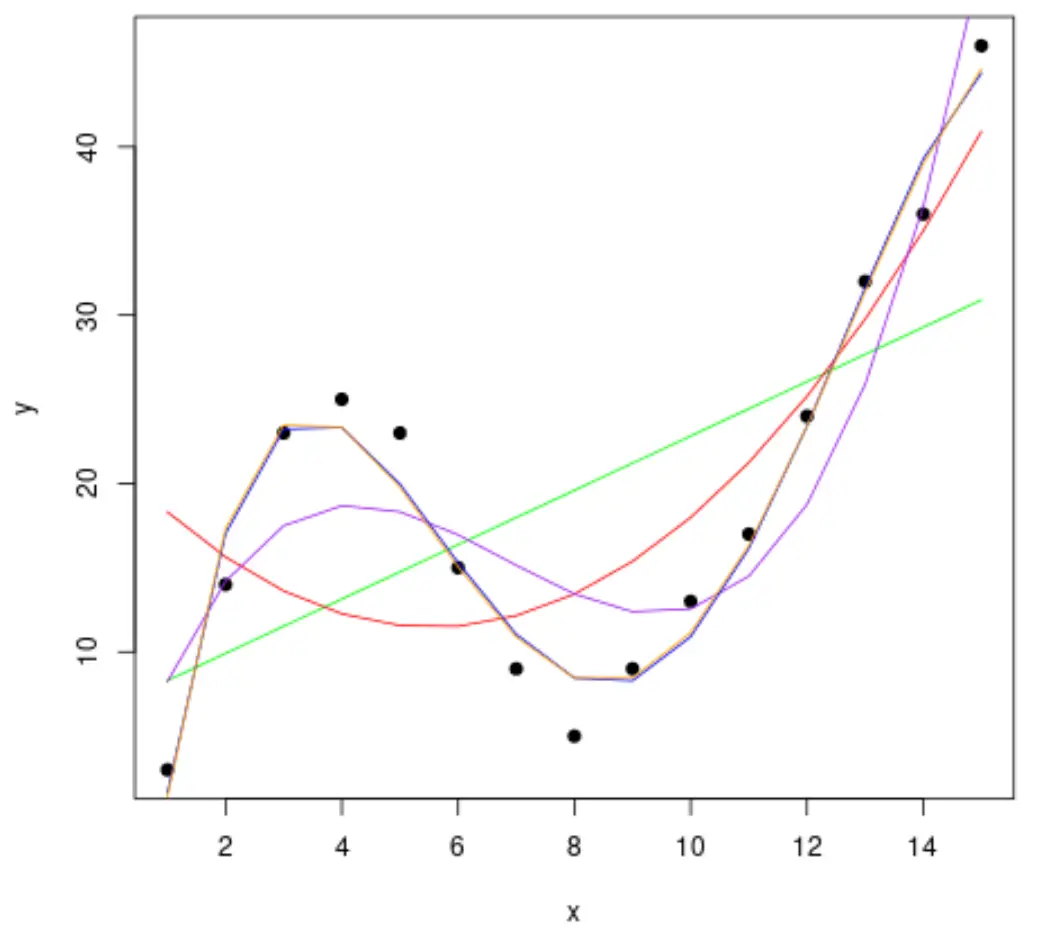
どの曲線がデータに最もよく適合するかを判断するには、各モデルの調整された R 二乗を確認します。
この値は、予測変数の数を調整した、モデル内の予測変数によって説明できる応答変数の変動のパーセンテージを示します。
#calculated adjusted R-squared of each model summary(fit1)$adj. r . squared summary(fit2)$adj. r . squared summary(fit3)$adj. r . squared summary(fit4)$adj. r . squared summary(fit5)$adj. r . squared [1] 0.3144819 [1] 0.5186706 [1] 0.7842864 [1] 0.9590276 [1] 0.9549709
結果から、調整された R 二乗が最も高いモデルは、調整された R 二乗が0.959である 4 次多項式であることがわかります。
ステップ 3: 最終的な曲線を視覚化する
最後に、4 次多項式モデルの曲線を使用して散布図を作成できます。
#create a scatterplot of x vs. y plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ') #define x-axis values x_axis <- seq(1, 15, length= 15 ) #add curve of fourth-degree polynomial model lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')

summary()関数を使用して、この行の方程式を取得することもできます。
summary(fit4)
Call:
lm(formula = y ~ poly(x, 4, raw = TRUE), data = df)
Residuals:
Min 1Q Median 3Q Max
-3.4490 -1.1732 0.6023 1.4899 3.0351
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -26.51615 4.94555 -5.362 0.000318 ***
poly(x, 4, raw = TRUE)1 35.82311 3.98204 8.996 4.15e-06 ***
poly(x, 4, raw = TRUE)2 -8.36486 0.96791 -8.642 5.95e-06 ***
poly(x, 4, raw = TRUE)3 0.70812 0.08954 7.908 1.30e-05 ***
poly(x, 4, raw = TRUE)4 -0.01924 0.00278 -6.922 4.08e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.424 on 10 degrees of freedom
Multiple R-squared: 0.9707, Adjusted R-squared: 0.959
F-statistic: 82.92 on 4 and 10 DF, p-value: 1.257e-07
曲線の方程式は次のとおりです。
y = -0.0192x 4 + 0.7081x 3 – 8.3649x 2 + 35.823x – 26.516
この方程式を使用すると、モデル内の予測変数に基づいて応答変数の値を予測できます。たとえば、 x = 4 の場合、 y = 23.34と予測します。
y = -0.0192(4) 4 + 0.7081(4) 3 – 8.3649(4) 2 + 35.823(4) – 26.516 = 23.34