R でボンフェローニ補正を実行する方法

一元配置分散分析は、 3 つ以上の独立したグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

ANOVA 表全体のp 値が一定の有意性レベルを下回っている場合、グループ平均の少なくとも 1 つが他の平均とは異なると言える十分な証拠があります。

ただし、これではどのグループが互いに異なるかは分かりません。これは単に、すべてのグループの平均が等しいわけではないことを示しています。

どのグループが互いに異なっているかを正確に知るには、 家族ごとの誤り率を制御しながら、各グループ間でペアごとの t 検定を実行する必要があります。

これを実現する最も一般的な方法の 1 つは、各ペアワイズ t 検定の p 値を計算するときにボンフェローニ補正を使用することです。

このチュートリアルでは、R でボンフェローニ補正を実行する方法について説明します。

例: R でのボンフェローニ補正

教師が、3 つの異なる学習方法が生徒間でテストの得点に差をもたらすかどうかを知りたいとします。

これをテストするために、彼女は 10 人の生徒をランダムに割り当てて、各学習テクニックを使用させました。割り当てられた学習方法を 1 週間使用した後、各生徒は同じ試験を受けます。

R の次の手順を使用して一元配置分散分析を近似し、ボンフェローニ補正を使用して各グループの検査結果間のペアごとの差を計算できます。

ステップ 1: データセットを作成します。

次のコードは、30 人の学生全員の試験結果を含むデータセットを作成する方法を示しています。

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

ステップ 2: 各グループの試験結果を表示します。

次のコードは、箱ひげ図を作成して各グループの検査結果の分布を視覚化する方法を示しています。

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

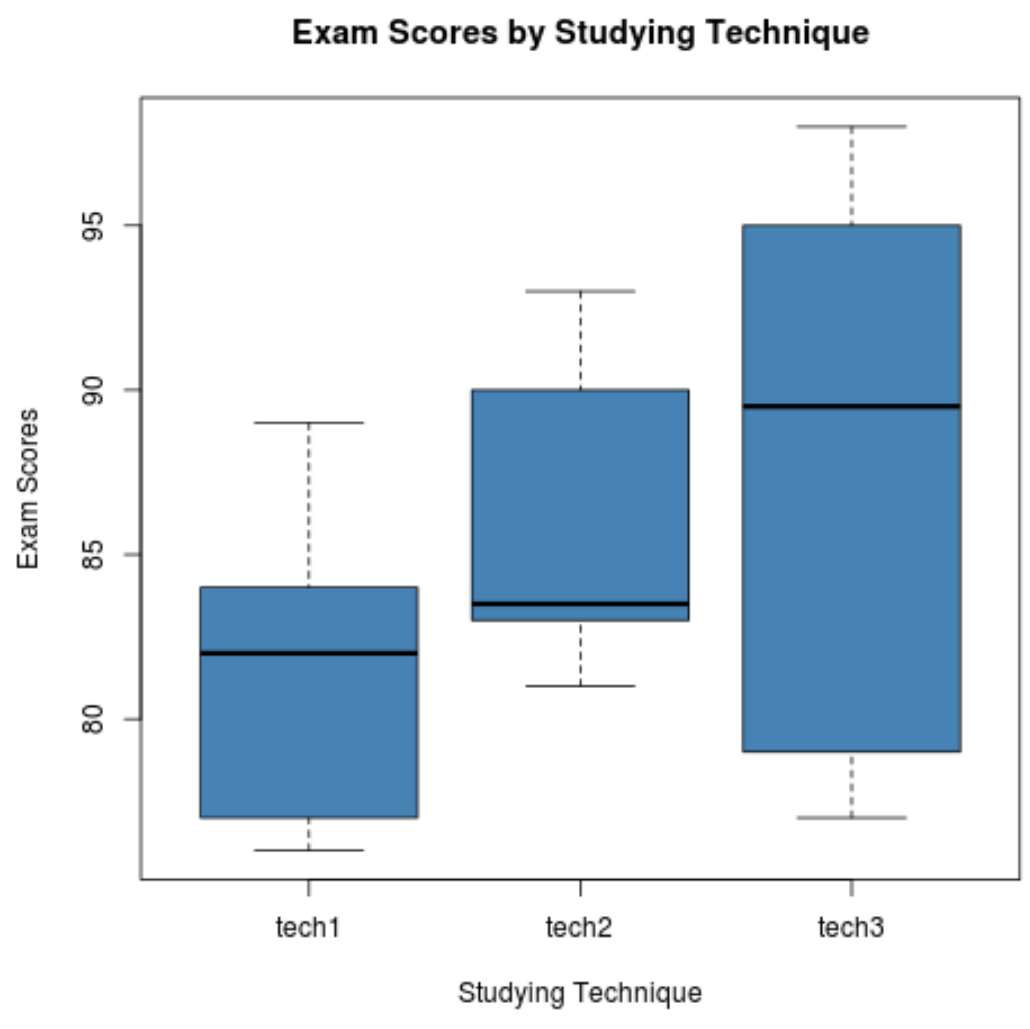
ステップ 3: 一元配置分散分析を実行します。

次のコードは、一元配置分散分析を実行して、各グループの平均試験得点間の差異をテストする方法を示しています。

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

全体の p 値 ( 0.0476 ) は 0.05 未満であるため、これは各グループの試験平均点が同じではないことを示しています。

次に、p 値のボンフェローニ補正を使用してペアごとの t 検定を実行し、各グループの検査結果間のペアごとの差異を計算します。

ステップ 4: ペアごとの t 検定を実行します。

R でボンフェローニ補正を使用してペアワイズ t 検定を実行するには、次の構文を使用するpariwise.t.test()関数を使用できます。

ペアワイズ.t.test(x, g, p.adjust.method=”ボンフェローニ”)

金：

• x:応答値の数値ベクトル
• g:グループの名前を指定するベクトル (例: 学習テクニック)

次のコードは、この例でこの関数を使用する方法を示しています。

 #perform pairwise t-tests with Bonferroni's correction
pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ")

	Pairwise comparisons using t tests with pooled SD 

data: data$score and data$technique 

      tech1 tech2
tech2 0.309 -    
tech3 0.048 1.000

P value adjustment method: bonferroni

結果を解釈する方法は次のとおりです。

• テクニック 1 とテクニック 2 の間の試験スコアの平均差の調整済み p 値は0.309です。
• テクニック 1 とテクニック 3 の間の試験スコアの平均差の調整された p 値は0.048です。
• テクニック 2 とテクニック 3 の間の試験スコアの平均差の調整された p 値は1000です。

結果に基づくと、唯一の有意な違いはテクニック 1 とテクニック 3 の間にあることがわかります。

追加リソース

一元配置分散分析の概要
R で一元配置分散分析を実行する方法
R で Tukey テストを実行する方法
R でダネットのテストを実行する方法