R でランダム フォレストを作成する方法 (ステップバイステップ)

一連の予測変数と応答変数の間の関係が非常に複雑な場合、多くの場合、非線形手法を使用してそれらの間の関係をモデル化します。

そのような方法の 1 つは、 決定ツリーを構築することです。ただし、単一の決定木を使用する場合の欠点は、 分散が大きくなる傾向があることです。

つまり、データセットを 2 つの半分に分割し、両方の半分にデシジョン ツリーを適用すると、結果は大きく異なる可能性があります。

単一のデシジョン ツリーの分散を減らすために使用できる 1 つの方法は、次のように動作するランダム フォレスト モデルを構築することです。

1.元のデータセットからb 個のブートストラップ サンプルを取得します。

2.各ブートストラップ サンプルのデシジョン ツリーを作成します。

• ツリーを構築するとき、分割が考慮されるたびに、 m 個の予測子のランダムなサンプルのみが、 p 個の予測子の完全なセットから分割の候補とみなされます。一般に、 √pに等しいmを選択します。

3.各ツリーからの予測を平均して、最終モデルを取得します。

ランダム フォレストは、単一のデシジョン ツリーやさらには袋詰めされたモデルよりもはるかに正確なモデルを生成する傾向があることがわかりました。

このチュートリアルでは、R でデータセットのランダム フォレスト モデルを作成する方法の例を段階的に説明します。

ステップ 1: 必要なパッケージをロードする

まず、この例に必要なパッケージをロードします。この単純な例では、必要なパッケージは 1 つだけです。

 library (randomForest)

ステップ 2: ランダム フォレスト モデルを調整する

この例では、153 日にわたるニューヨーク市の大気質の測定値を含む、 Air Qualityという組み込みの R データセットを使用します。

 #view structure of air quality dataset
str(airquality)

'data.frame': 153 obs. of 6 variables:
 $ Ozone: int 41 36 12 18 NA 28 23 19 8 NA ...
 $Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
 $ Wind: num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
 $ Temp: int 67 72 74 62 56 66 65 59 61 69 ...
 $Month: int 5 5 5 5 5 5 5 5 5 5 ...
 $Day: int 1 2 3 4 5 6 7 8 9 10 ...

#find number of rows with missing values
sum(! complete . cases (airquality))

[1] 42

このデータセットには欠損値を含む行が 42 行あります。したがって、ランダム フォレスト モデルを当てはめる前に、各列の欠損値を列の中央値で埋めます。

 #replace NAs with column medians
for (i in 1: ncol (air quality)) {
  airquality[,i][ is . na (airquality[, i])] <- median (airquality[, i], na . rm = TRUE )
}

関連: R で欠損値を代入する方法

次のコードは、 randomForestパッケージのrandomForest()関数を使用して、R でランダム フォレスト モデルを近似する方法を示しています。

 #make this example reproducible
set.seed(1)

#fit the random forest model
model <- randomForest(
  formula = Ozone ~ .,
  data = airquality
)

#display fitted model
model

Call:
 randomForest(formula = Ozone ~ ., data = airquality) 
               Type of random forest: regression
                     Number of trees: 500
No. of variables tried at each split: 1

          Mean of squared residuals: 327.0914
                    % Var explained: 61

#find number of trees that produce lowest test MSE
which.min(model$mse)

[1] 82

#find RMSE of best model
sqrt(model$mse[ which . min (model$mse)]) 

[1] 17.64392

結果から、最も低いテスト平均二乗誤差 (MSE) を生成したモデルでは82 個のツリーが使用されていることがわかります。

このモデルの二乗平均平方根誤差が17.64392であることもわかります。これは、オゾンの予測値と実際の観測値の平均差と考えることができます。

次のコードを使用して、使用される木の数に基づいて MSE テストのプロットを生成することもできます。

 #plot the MSE test by number of trees
plot(model)

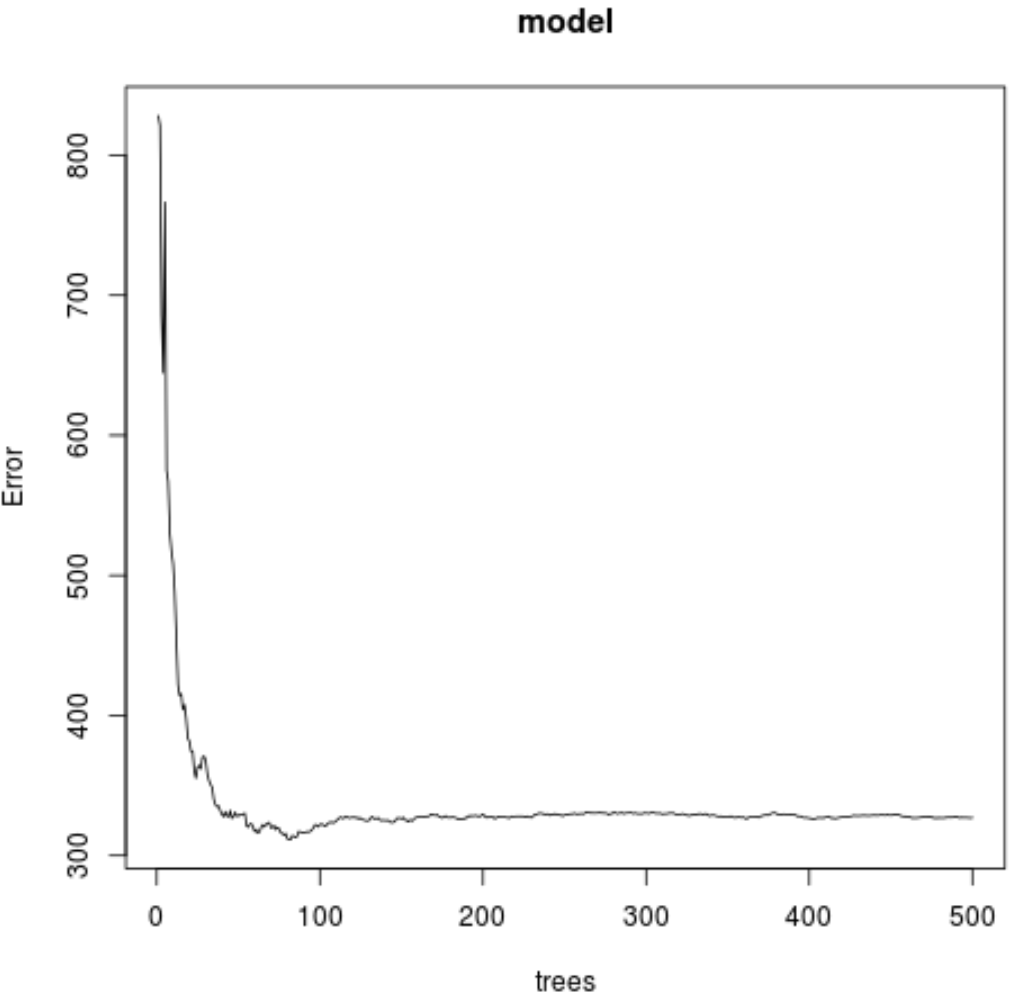
そして、 varImpPlot()関数を使用して、最終モデルにおける各予測子変数の重要性を表示するプロットを作成できます。

 #produce variable importance plot
varImpPlot(model) 

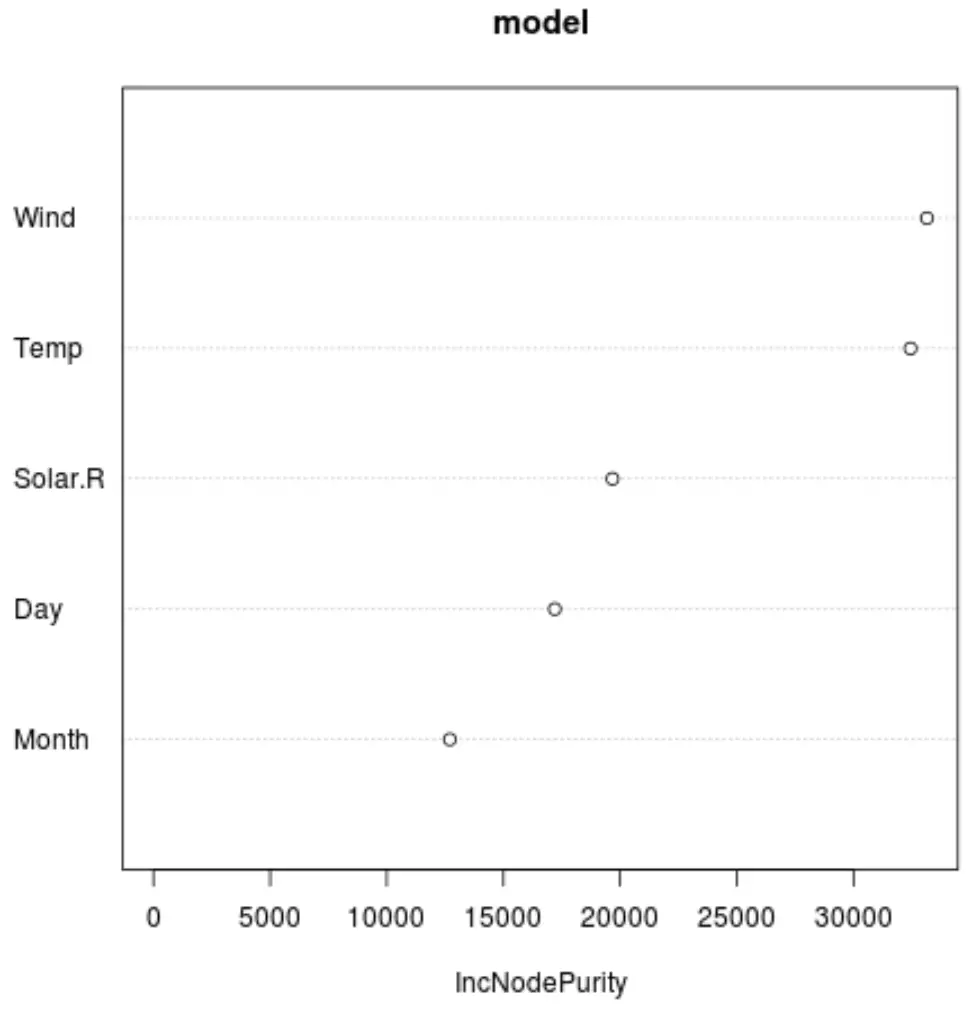
X 軸は、回帰ツリーのノード純度の平均増加を、Y 軸に表示されたさまざまな予測変数間の分割の関数として表示します。

グラフから、 Wind が最も重要な予測変数であり、それに僅差でTempが続くことがわかります。

ステップ 3: モデルを調整する

デフォルトでは、 randomForest()関数は、各分割の潜在的な候補として 500 個のツリーと (予測子の総数/3) 個のランダムに選択された予測子を使用します。これらのパラメータは、 tuneRF()関数を使用して調整できます。

次のコードは、次の仕様を使用して最適なモデルを見つける方法を示しています。

• ntreeTry:構築するツリーの数。
• mtryStart:各分割で考慮される予測子変数の初期数。
• stepFactor:推定される out-of-bag エラーが一定量改善しなくなるまで増加する係数。
• 改善:ステップ係数を増加し続けるためにバッグ出口エラーを改善する必要がある量。

 model_tuned <- tuneRF(
               x=airquality[,-1], #define predictor variables
               y=airquality$Ozone, #define response variable
               ntreeTry= 500 ,
               mtryStart= 4 , 
               stepFactor= 1.5 ,
               improve= 0.01 ,
               trace= FALSE #don't show real-time progress
               )

この関数は次のプロットを生成します。このプロットには、ツリーを構築するときに各分割で使用される予測子の数が X 軸に、推定されたバッグ外誤差が Y 軸に表示されます。

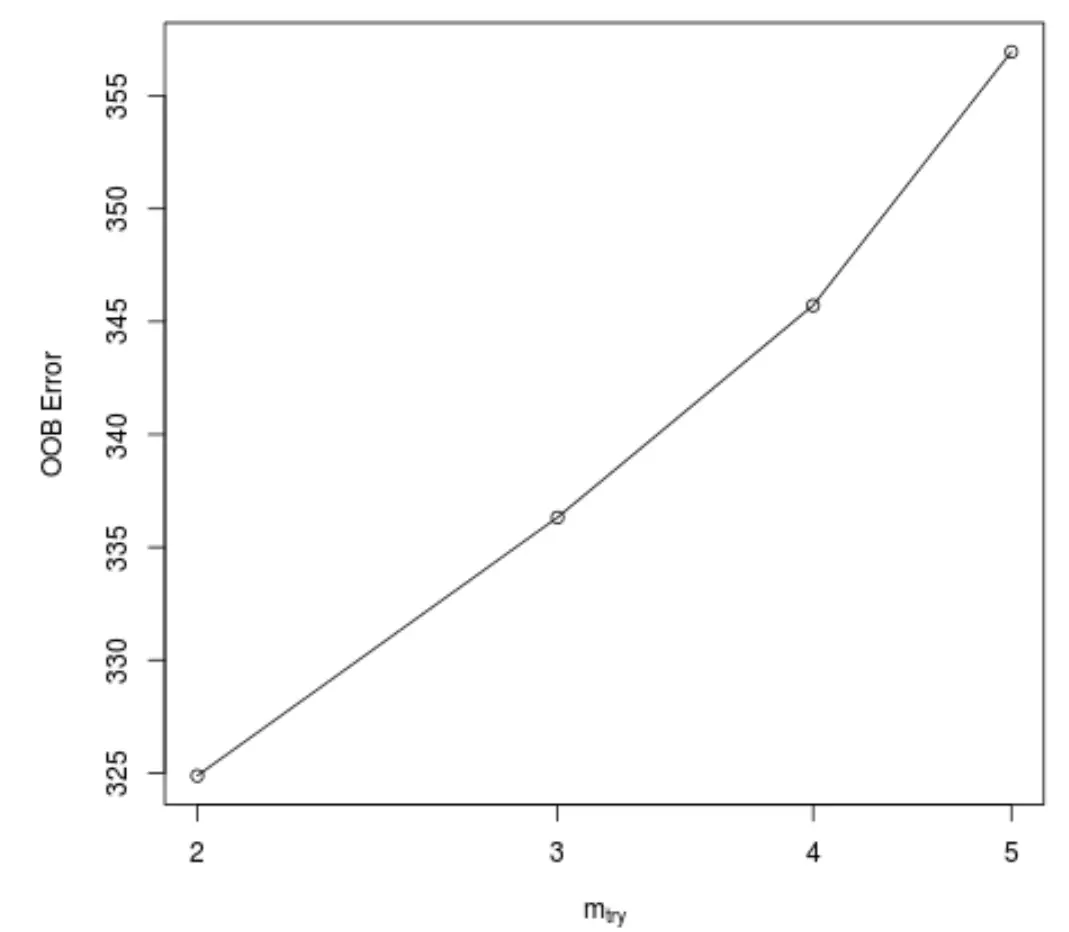
ツリーを構築するときに、各分割でランダムに選択された2 つの予測子を使用することで、最小の OOB エラーが得られることがわかります。

これは実際には、最初のrandomForest()関数で使用されるデフォルト設定(合計予測値/3 = 6/3 = 2)に対応します。

ステップ 4: 最終モデルを使用して予測を行う

最後に、調整されたランダム フォレスト モデルを使用して、新しい観測値についての予測を行うことができます。

 #define new observation
new <- data.frame(Solar.R=150, Wind=8, Temp=70, Month=5, Day=5)

#use fitted bagged model to predict Ozone value of new observation
predict(model, newdata=new)

27.19442

予測変数の値に基づいて、適合されたランダム フォレスト モデルは、この特定の日のオゾン値が27.19442になると予測します。

この例で使用されている完全な R コードは、 ここにあります。