R で lm() 関数を使用して線形モデルを近似する方法
R のlm()関数は、線形回帰モデルを近似するために使用されます。
この関数は次の基本構文を使用します。
lm(式、データ、…)
金:
- 式:線形モデルの式 (例: y ~ x1 + x2)
- data:データを含むデータ ブロックの名前
次の例は、R でこの関数を使用して次のことを行う方法を示しています。
- 回帰モデルを当てはめる
- 回帰モデルの適合性の概要を表示する
- モデル診断プロットを表示する
- 近似回帰モデルをプロットする
- 回帰モデルを使用して予測を行う
回帰モデルを当てはめる
次のコードは、 lm()関数を使用して R で線形回帰モデルを近似する方法を示しています。
#define data df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12), y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22)) #fit linear regression model using 'x' as predictor and 'y' as response variable model <- lm(y ~ x, data=df)
回帰モデルの概要を表示
次に、 summary()関数を使用して、回帰モデルの適合の概要を表示します。
#view summary of regression model
summary(model)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-4.4793 -0.9772 -0.4772 1.4388 4.6328
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675
モデル内の最も重要な値を解釈する方法は次のとおりです。
- F 統計量= 18.35、対応するp 値= 0.002675。この p 値は 0.05 未満であるため、モデル全体としては統計的に有意です。
- 複数の R の 2 乗= 0.6964。これは、応答変数 y の変動の 69.64% が予測変数 x によって説明できることがわかります。
- x の推定係数: 1.2780。これは、x の各追加単位の増加が y の平均 1.2780 の増加に関連していることを示しています。
次に、出力からの係数推定値を使用して、推定回帰式を作成できます。
y = 11.1432 + 1.2780*(x)
おまけ: R での回帰出力の各値を解釈するための完全なガイドは、 ここで見つけることができます。
モデル診断プロットを表示する
次に、 plot()関数を使用して、回帰モデルの診断プロットをプロットします。
#create diagnostic plots
plot(model)
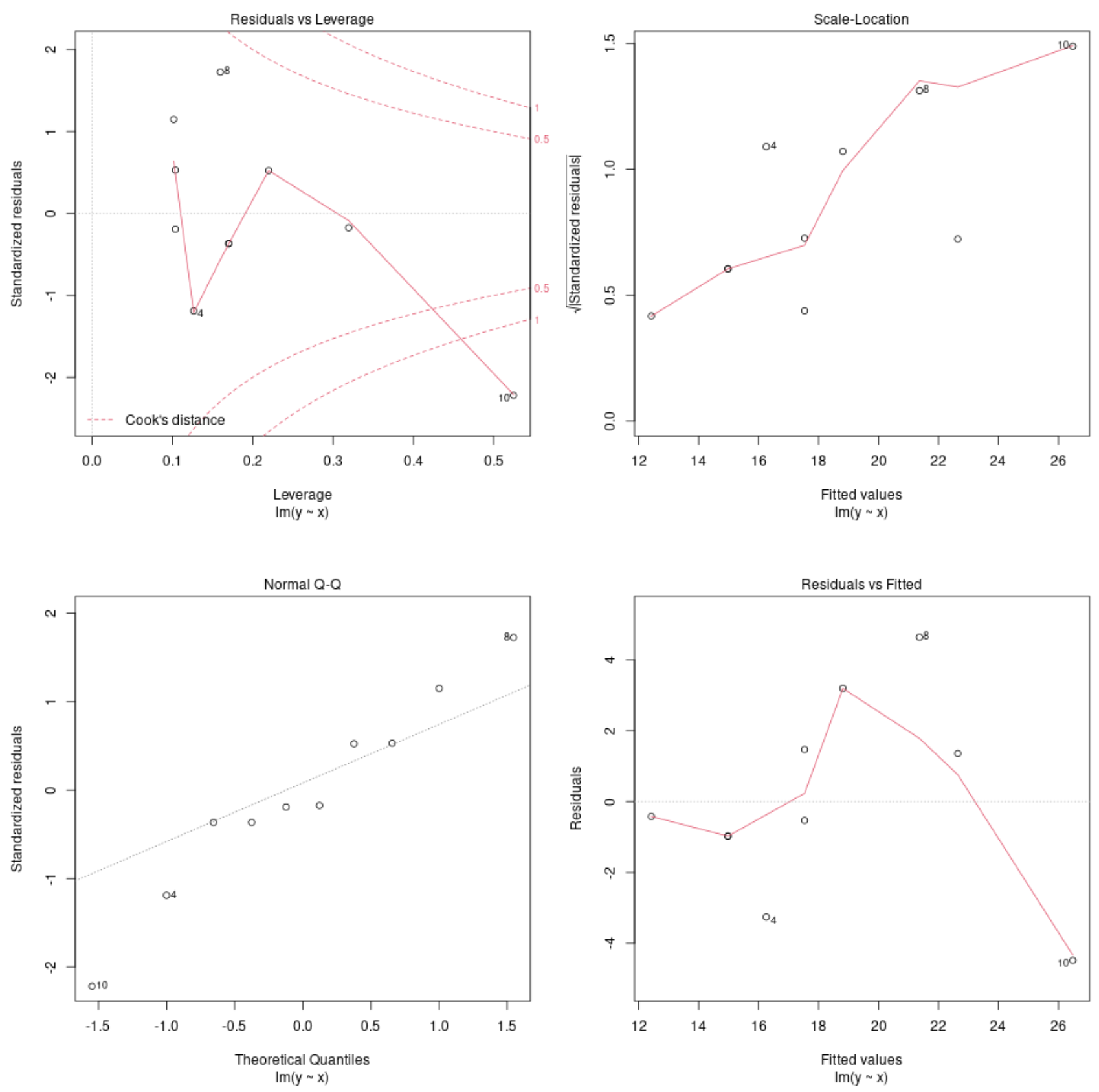
これらのグラフを使用すると、回帰モデルの残差を分析して、モデルがデータに使用するのが適切かどうかを判断できます。
R でモデルの診断プロットを解釈する方法の完全な説明については、このチュートリアルを参照してください。
近似回帰モデルをプロットする
abline()関数を使用して、近似回帰モデルをプロットできます。
#create scatterplot of raw data plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ') #add fitted regression line abline(model)
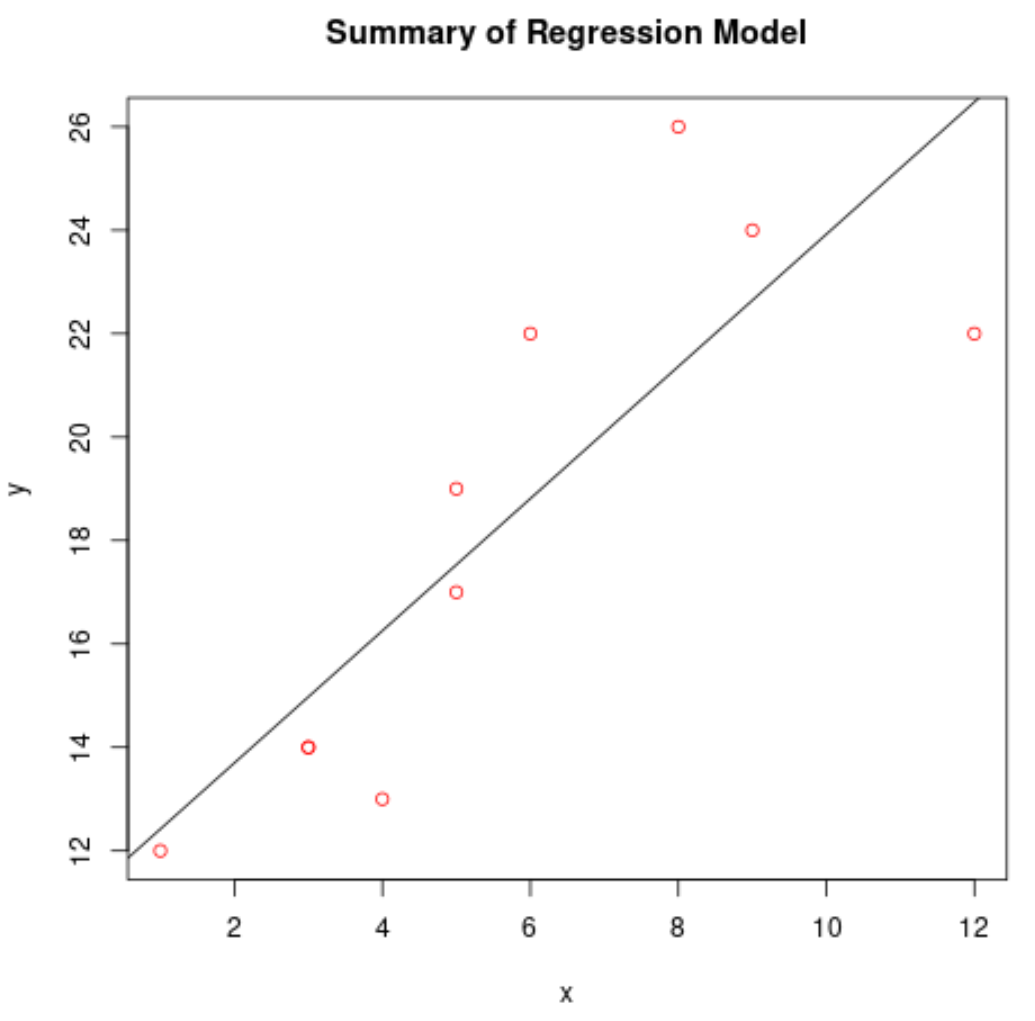
回帰モデルを使用して予測を行う
detect()関数を使用して、新しい観測値の応答値を予測できます。
#define new observation
new <- data. frame (x=c(5))
#use the fitted model to predict the value for the new observation
predict(model, newdata = new)
1
17.5332
モデルは、この新しい観測値の応答値が17.5332になると予測します。