R でのなげなわ回帰 (ステップバイステップ)

ラッソ回帰は、データに多重共線性が存在する場合に回帰モデルを近似するために使用できる方法です。

簡単に言うと、最小二乗回帰は、残差二乗和 (RSS) を最小化する係数推定値を見つけようとします。

RSS = Σ(y _i – ŷ _i )2

金：

• Σ : 和を意味するギリシャ語の記号
• y _i : ^{i 番目の}観測値の実際の応答値
• ŷ _i : 重回帰モデルに基づく予測応答値

逆に、なげなわ回帰では、以下を最小限に抑えようとします。

RSS + λΣ|β _j |

ここで、 jは 1 からp 個の予測子変数であり、λ ≥ 0 です。

方程式のこの 2 番目の項は、撤退ペナルティとして知られています。ラッソ回帰では、可能な限り最小の MSE (平均二乗誤差) テストを生成する λ の値を選択します。

このチュートリアルでは、R でなげなわ回帰を実行する方法の段階的な例を示します。

ステップ 1: データをロードする

この例では、 mtcarsという R の組み込みデータセットを使用します。応答変数としてhp を使用し、予測変数として次の変数を使用します。

• mpg
• 重さ
• たわごと
• qsec

ラッソ回帰を実行するには、 glmnetパッケージの関数を使用します。このパッケージでは、 応答変数がベクトルであること、および予測子変数のセットがdata.matrixクラスのものであることが必要です。

次のコードは、データを定義する方法を示しています。

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

ステップ 2:なげなわ回帰モデルを当てはめる

次に、 glmnet()関数を使用して、なげなわ回帰モデルを近似し、 alpha=1を指定します。

アルファを 0 に設定することはリッジ回帰を使用することと同等であり、アルファを 0 から 1 までの値に設定することは弾性ネットを使用することと同等であることに注意してください。  

ラムダにどの値を使用するかを決定するために、k 分割交差検証を実行し、最小の検定平均二乗誤差 (MSE) を生成するラムダ値を特定します。

cv.glmnet()関数は、k = 10 回を使用して k 分割相互検証を自動的に実行することに注意してください。

 library (glmnet)

#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 1 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 5.616345

#produce plot of test MSE by lambda value
plot(cv_model) 

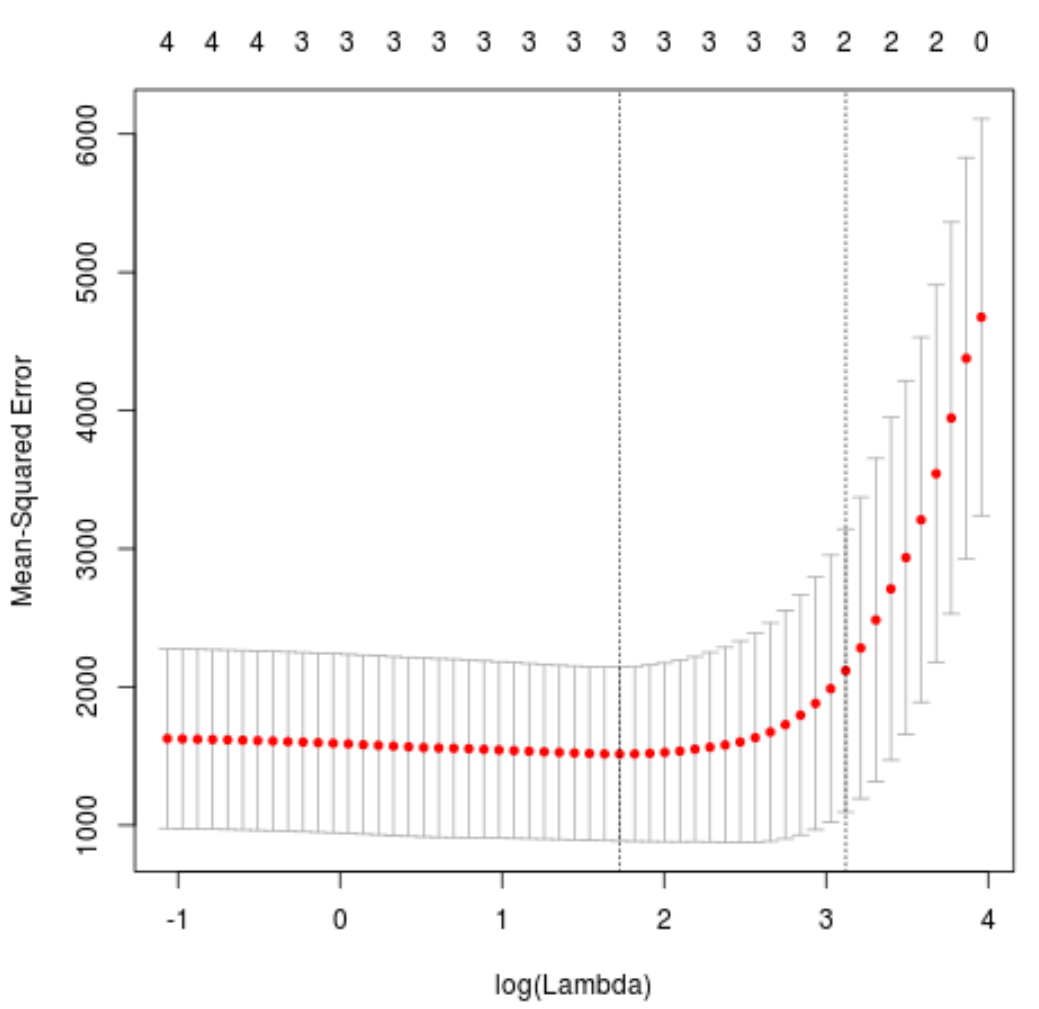
MSE テストを最小化するラムダ値は5.616345であることがわかります。

ステップ 3: 最終モデルを分析する

最後に、最適なラムダ値によって生成された最終モデルを分析できます。

次のコードを使用して、このモデルの係数推定値を取得できます。

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 1 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) 484.20742
mpg -2.95796
wt 21.37988
drat.      
qsec -19.43425

ラッソ回帰により係数がゼロになったため、 drat予測子の係数は表示されません。これは、彼が十分な影響力を持っていなかったため、モデルから完全に削除されたことを意味します。

これがリッジ回帰となげなわ回帰の重要な違いであることに注意してください。リッジ回帰ではすべての係数がゼロに向かって減少しますが、ラッソ回帰では係数が完全にゼロになることでモデルから予測子が削除される可能性があります。

最終的ななげなわ回帰モデルを使用して、新しい観測値についての予測を行うこともできます。たとえば、次の属性を持つ新車があるとします。

• mpg: 24
• 重量: 2.5
• 価格: 3.5
• qsec: 18.5

次のコードは、適合したなげなわ回帰モデルを使用して、この新しい観測値のhp値を予測する方法を示しています。

 #define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow= 1 , ncol= 4 ) 

#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)

[1,] 109.0842

入力された値に基づいて、モデルはこの車の馬力値が109.0842であると予測します。

最後に、トレーニング データに対する モデルの R 二乗を計算できます。

 #use fitted best model to make predictions
y_predicted <- predict (best_model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.8047064

R の 2 乗は0.8047064となります。つまり、最良のモデルはトレーニング データの応答値の変動の80.47%を説明できました。

この例で使用されている完全な R コードは、 ここで見つけることができます。