R でウェルチの t 検定を実行する方法

ウェルチの t 検定は、 2 つのグループの分散が等しいと想定されていない場合に、2 つの独立したグループ間の平均を比較するために使用されます。

R でウェルチの t 検定を実行するには、次の構文を使用するt.test()関数を使用できます。

t.test(x, y, 代替 = c(“2 つの顔”, “少ない”, “大きい”))

金：

• x:最初のグループのデータ値の数値ベクトル
• y: 2 番目のグループのデータ値の数値ベクトル
• 代替:テストの対立仮説。デフォルトは両面です。

次の例は、この関数を使用して R でウェルチの t 検定を実行する方法を示しています。

例: R でのウェルチの t 検定

教師は、試験準備のためにテスト対策冊子を使用した 12 人の生徒と、使用しなかった 12 人の生徒の試験結果を比較したいと考えています。

次のベクトルは、各グループの学生の試験結果を示しています。

 booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

ウェルチの t 検定を実行する前に、まず 箱ひげ図を作成して各グループのスコアの分布を視覚化できます。

 boxplot(booklet, no_booklet, names =c(" Booklet "," No Booklet "))

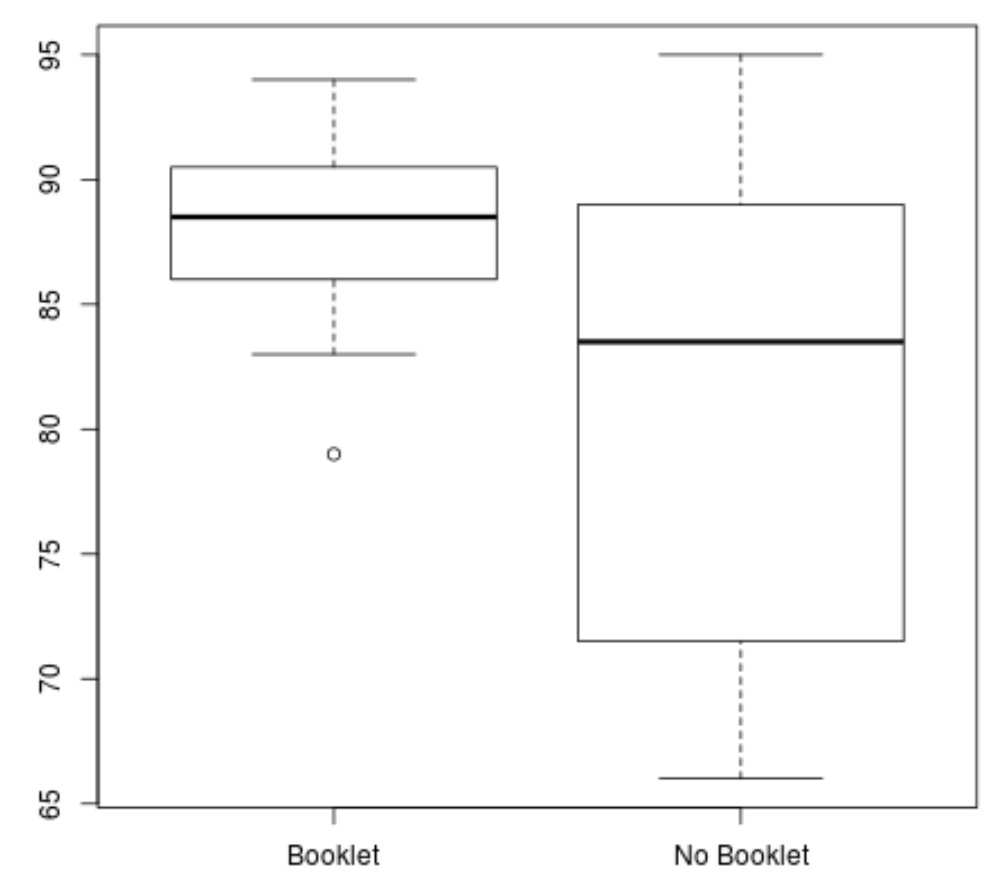
「ブックレット」グループの平均スコアが高く、スコアの分散が低いことがはっきりとわかります。

グループ間の平均スコアが有意に異なるかどうかを正式に検定するには、ウェルチの t 検定を実行できます。

 #perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667 80.83333 

結果から、 t検定統計量は2.2361で、対応する p 値は0.04171であることがわかります。

この p 値は 0.05 未満であるため、帰無仮説を棄却し、2 つのグループ間の試験の平均得点には統計的に有意な差があると結論付けることができます。

t.test()関数は、次の情報も提供します。

• 2 つのグループ間の平均試験得点の差の 95%信頼区間は[0.3048, 13.8618 ] です。
• 最初のグループの平均試験スコアは87.91667です。
• 2 番目のグループの試験の平均スコアは80.83333です。

t.test() 関数の完全なドキュメントはここで見つけることができます。

追加リソース

次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。

R で 1 サンプルの t 検定を実行する方法
R で 2 サンプルの t 検定を実行する方法
R で対応のあるサンプルの t 検定を実行する方法
R で 1 つのグラフに複数の箱ひげ図をプロットする方法