R での主成分回帰 (ステップバイステップ)

p個の予測子変数のセットと応答変数が与えられると、多重線形回帰では最小二乗法として知られる方法を使用して残差二乗和 (RSS) を最小化します。

RSS = Σ(y _i – ŷ _i ) ²

金：

• Σ : 和を意味するギリシャ語の記号
• y _i : ^{i 番目の}観測値の実際の応答値
• ŷ _i : 重回帰モデルに基づく予測応答値

ただし、予測変数の相関性が高い場合、 多重共線性が問題になる可能性があります。これにより、モデルの係数推定の信頼性が低くなり、大きな分散が示される可能性があります。

この問題を回避する 1 つの方法は、主成分回帰を使用することです。これは、元のp個の予測子のM 個の線形結合 (「主成分」と呼ばれます) を見つけ、最小二乗を使用して、主成分を予測子として使用して線形回帰モデルを近似します。

このチュートリアルでは、R で主成分回帰を実行する方法の段階的な例を示します。

ステップ 1: 必要なパッケージをロードする

R で主成分回帰を実行する最も簡単な方法は、 plsパッケージの関数を使用することです。

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

ステップ 2: PCR モデルを調整する

この例では、さまざまなタイプの車のデータが含まれるmtcarsという組み込みの R データセットを使用します。

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

この例では、 応答変数としてhpを使用し、予測変数として次の変数を使用して主成分回帰 (PCR) モデルを近似します。

• mpg
• 画面
• たわごと
• 重さ
• qsec

次のコードは、PCR モデルをこのデータに適合させる方法を示しています。次の引数に注意してください。

• scale=TRUE : これは、各予測子変数が平均 0、標準偏差 1 になるようにスケーリングする必要があることを R に指示します。これにより、予測子変数が異なる単位で測定された場合に、モデルに過度の影響を与えることがなくなります。 。
• validation=”CV” : これは R にk 分割相互検証を使用してモデルのパフォーマンスを評価するように指示します。これはデフォルトで k=10 のフォールドを使用することに注意してください。また、代わりに「LOOCV」を指定して、Leave-One-Out 相互検証を実行できることにも注意してください。

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

ステップ 3: 主要コンポーネントの数を選択する

モデルを調整したら、保持する価値のある主成分の数を決定する必要があります。

これを行うには、k-cross 検証によって計算されたテスト二乗平均平方根誤差 (テスト RMSE) を確認するだけです。

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: svdpc
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 44.56 35.64 35.83 36.23 36.67
adjCV 69.66 44.44 35.27 35.43 35.80 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 69.83 89.35 95.88 98.96 100.00
hp 62.38 81.31 81.96 81.98 82.03

結果には 2 つの興味深いテーブルがあります。

1. 検証: RMSEP

この表は、k 分割相互検証によって計算された RMSE テストを示しています。次のことがわかります。

• モデル内の元の項のみを使用した場合、テストの RMSE は69.66になります。
• 最初の主成分を追加すると、RMSE テストは44.56 に低下します。
• 2 番目の主成分を追加すると、RMSE テストは35.64 に低下します。

主成分を追加すると、実際にテストの RMSE が増加することがわかります。したがって、最終モデルでは 2 つの主成分のみを使用することが最適であると思われます。

2. トレーニング: 分散の % を説明する

この表は、主成分によって説明される応答変数の分散のパーセンテージを示しています。次のことがわかります。

• 最初の主成分のみを使用すると、応答変数の変動の69.83%を説明できます。
• 第 2 主成分を追加することで、応答変数の変動の89.35%を説明できます。

より多くの主成分を使用することでより多くの分散を説明できることに注意してください。ただし、2 つ以上の主成分を追加しても、実際には説明される分散のパーセンテージはそれほど増加しないことがわかります。

また、 validationplot()関数を使用して、RMSE テスト (MSE および R 二乗テストとともに) を主成分の数の関数として視覚化することもできます。

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type="MSEP")
validationplot(model, val.type="R2") 

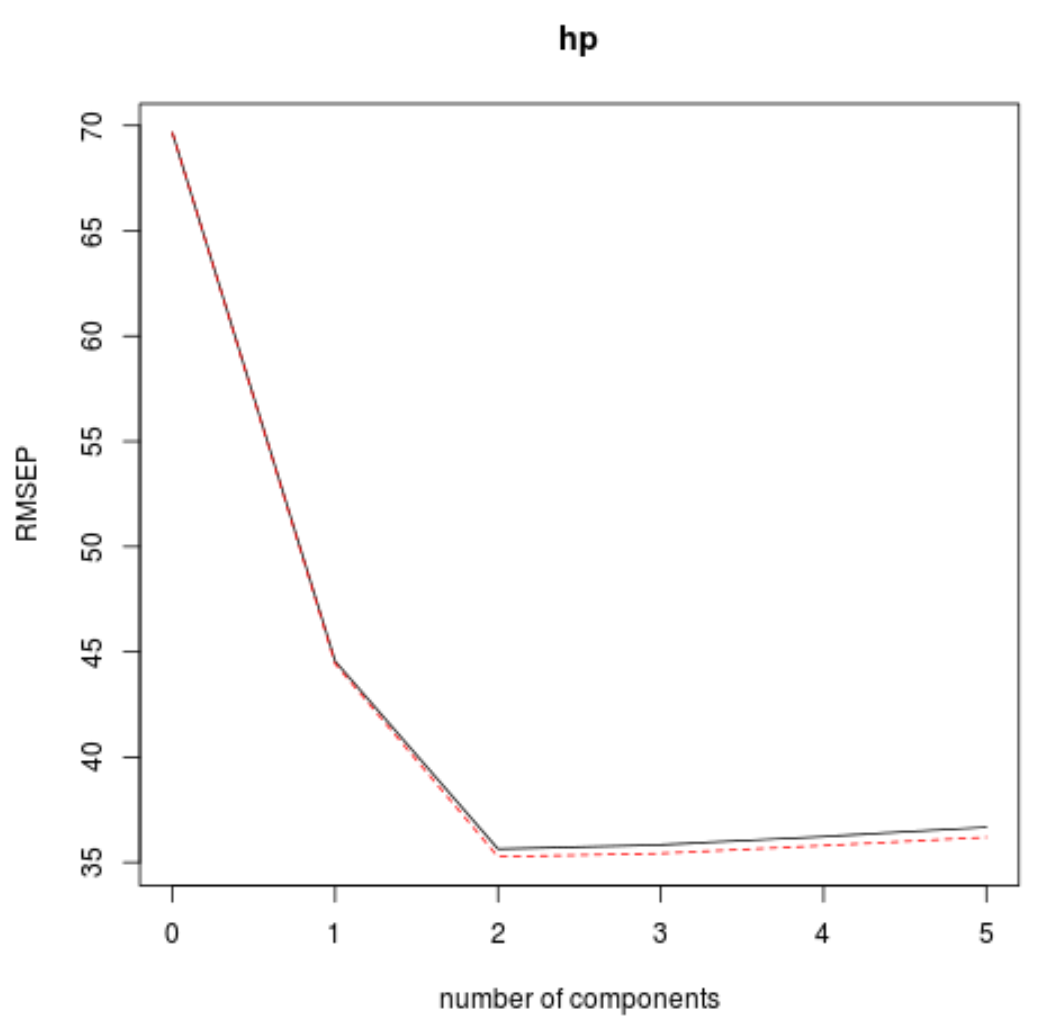
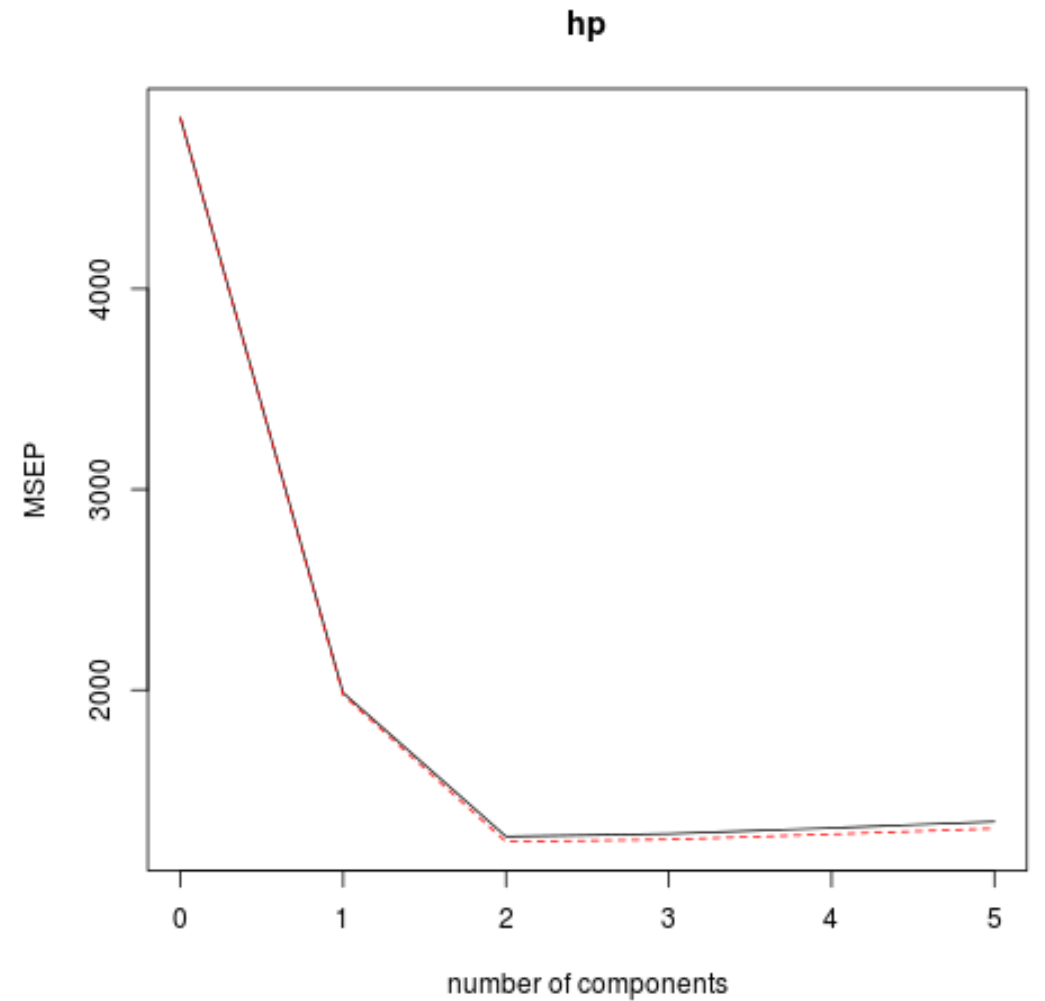
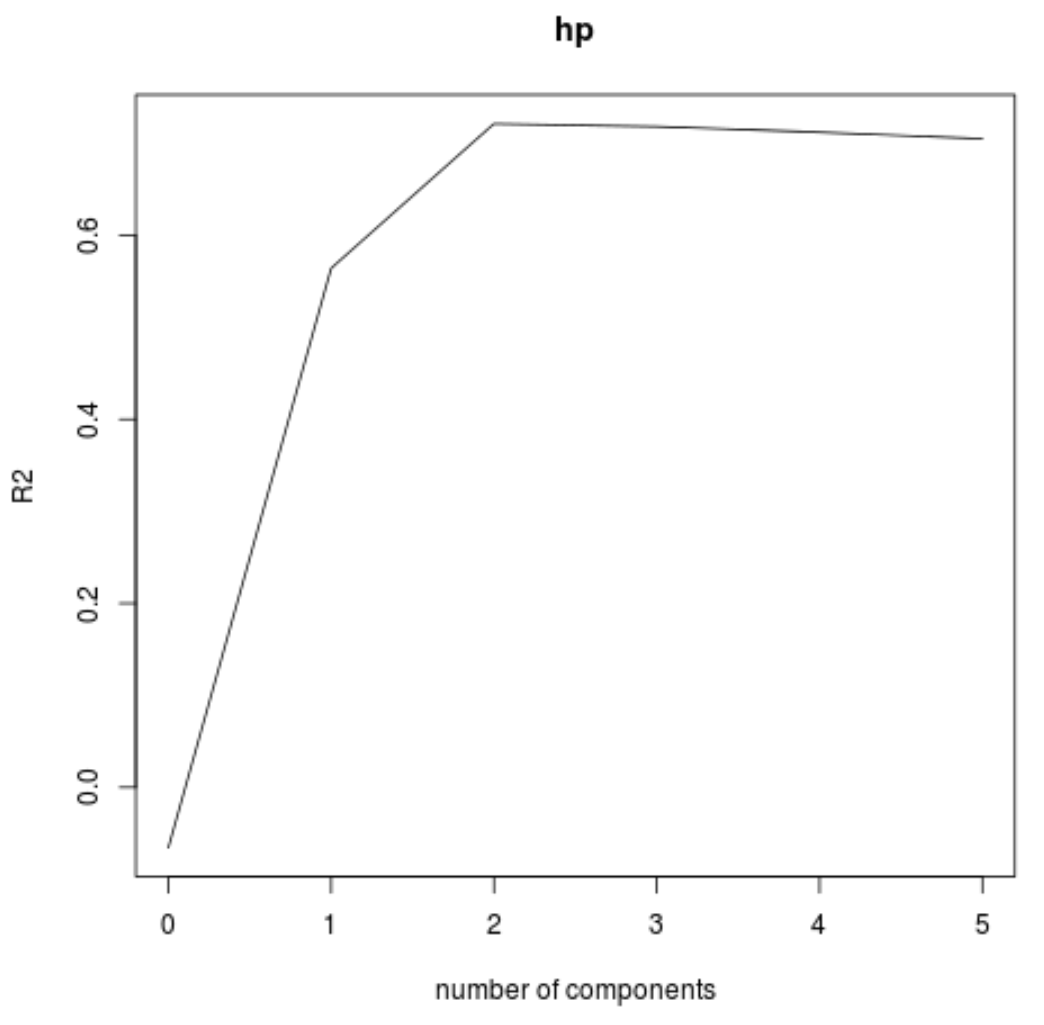
各グラフでは、2 つの主成分を追加するとモデルの適合性が向上しますが、さらに多くの主成分を追加するとモデルの適合性が低下する傾向があることがわかります。

したがって、最適なモデルには最初の 2 つの主成分のみが含まれます。

ステップ 4: 最終モデルを使用して予測を行う

最終的な 2 主成分 PCR モデルを使用して、新しい観測値についての予測を行うことができます。

次のコードは、元のデータセットをトレーニング セットとテスト セットに分割し、2 つの主成分を持つ PCR モデルを使用してテスト セットで予測を行う方法を示しています。

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 56.86549

テストの RMSE が56.86549であることがわかります。これは、テスト セットの観測値の予測hp値と観測されたhp値の間の平均偏差です。

この例での R コードの完全な使用法は、 ここで参照できます。