R で分位回帰を実行する方法
線形回帰は、1 つ以上の予測変数と応答変数の間の関係を理解するために使用できる方法です。
通常、線形回帰を実行するときは、応答変数の平均値を推定する必要があります。
ただし、代わりに分位点回帰として知られる方法を使用して、70 パーセンタイル、90 パーセンタイル、98 パーセンタイルなどの応答値の任意の分位値またはパーセンタイル値を推定することもできます。
R で分位回帰を実行するには、 quantregパッケージのrq()関数を使用できます。この関数は次の構文を使用します。
library (quantreg) model <- rq(y ~ x, data = dataset, tau = 0.5 )
金:
- y:応答変数
- x:予測変数
- データ:データセットの名前
- tau:検索するパーセンタイル。デフォルトは中央値 (tau = 0.5) ですが、0 から 1 までの任意の数値に設定できます。
このチュートリアルでは、この関数を使用して R で分位点回帰を実行する方法の段階的な例を示します。
ステップ 1: データを入力する
この例では、大学の 100 人の異なる学生の学習時間と得られた試験結果を含むデータセットを作成します。
#make this example reproducible set.seed(0) #create data frame hours <- runif(100, 1, 10) score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours) df <- data.frame(hours, score) #view first six rows head(df) hours score 1 9.070275 79.22682 2 3.389578 66.20457 3 4.349115 73.47623 4 6.155680 70.10823 5 9.173870 78.12119 6 2.815137 65.94716
ステップ 2: 分位点回帰を実行する
次に、学習時間を予測変数として、試験のスコアを応答変数として使用して、分位点回帰モデルを近似します。
このモデルを使用して、学習時間数に基づいて試験スコアの予想される 90 パーセンタイルを予測します。
library (quantreg) #fit model model <- rq(score ~ hours, data = df, tau = 0.9 ) #view summary of model summary(model) Call: rq(formula = score ~ hours, tau = 0.9, data = df) tau: [1] 0.9 Coefficients: coefficients lower bd upper bd (Intercept) 60.25185 59.27193 62.56459 hours 2.43746 1.98094 2.76989
結果から、推定された回帰式がわかります。
90 パーセンタイルの試験スコア = 60.25 + 2.437*(時間)
たとえば、8 時間勉強したすべての生徒の 90 パーセンタイル スコアは 79.75 になるはずです。
試験スコアの 90 パーセンタイル = 60.25 + 2.437*(8) = 79.75 。
出力には、予測子変数の切片と時間の信頼限界の上限と下限も表示されます。
ステップ 3: 結果を視覚化する
近似された分位点回帰式をグラフに重ねた散布図を作成して、回帰結果を視覚化することもできます。
library (ggplot2) #create scatterplot with quantile regression line ggplot(df, aes(hours,score)) + geom_point() + geom_abline(intercept= coef (model)[1], slope= coef (model)[2])
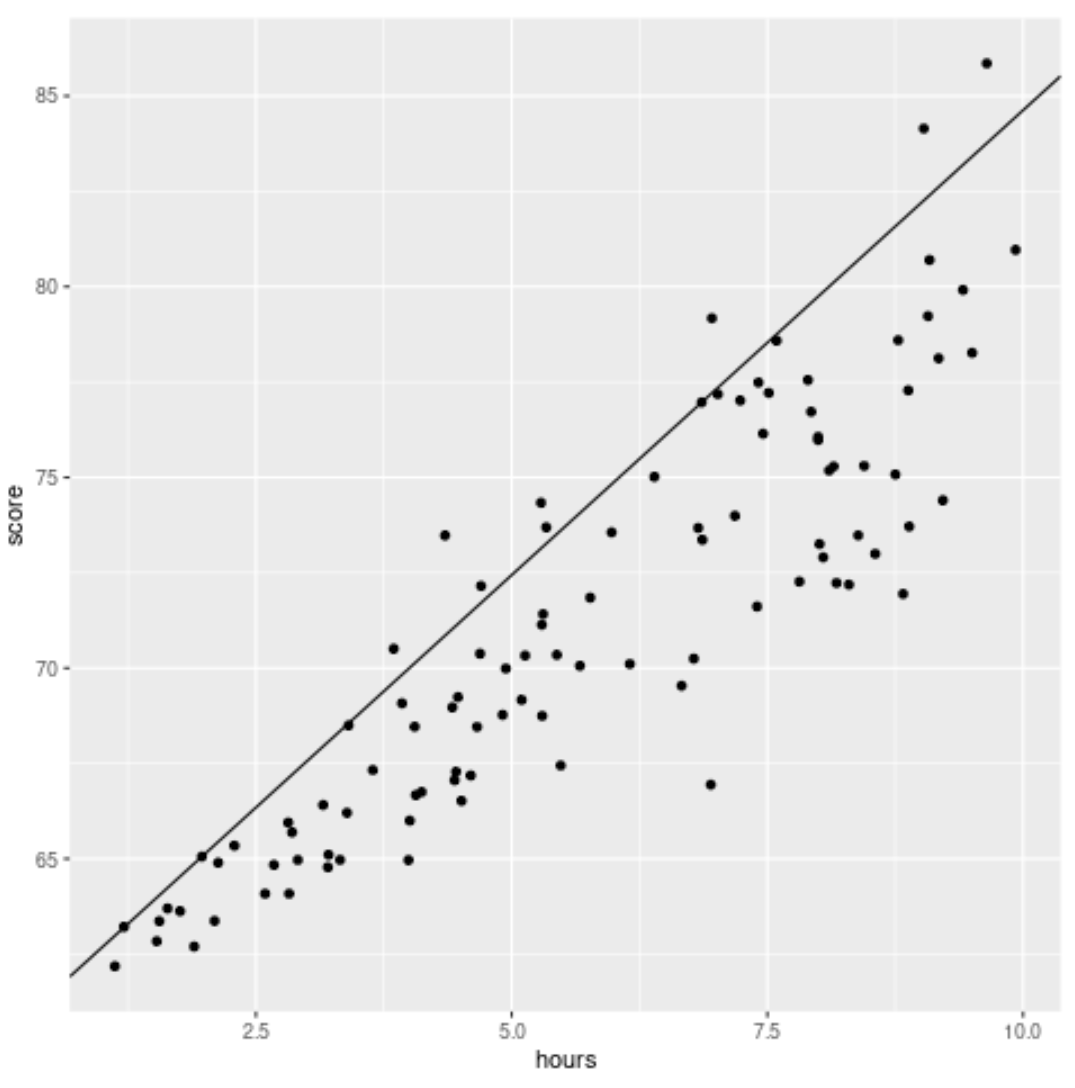
従来の線形回帰直線とは異なり、この近似直線はデータの中心を通過していないことに注意してください。代わりに、予測子変数の各レベルで推定された 90 パーセンタイルを通過します。
geom_smooth()引数を追加すると、近似された分位数回帰式と単純な線形回帰式の違いがわかります。
library (ggplot2) #create scatterplot with quantile regression line and simple linear regression line ggplot(df, aes(hours,score)) + geom_point() + geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) + geom_smooth(method=" lm ", se= F )
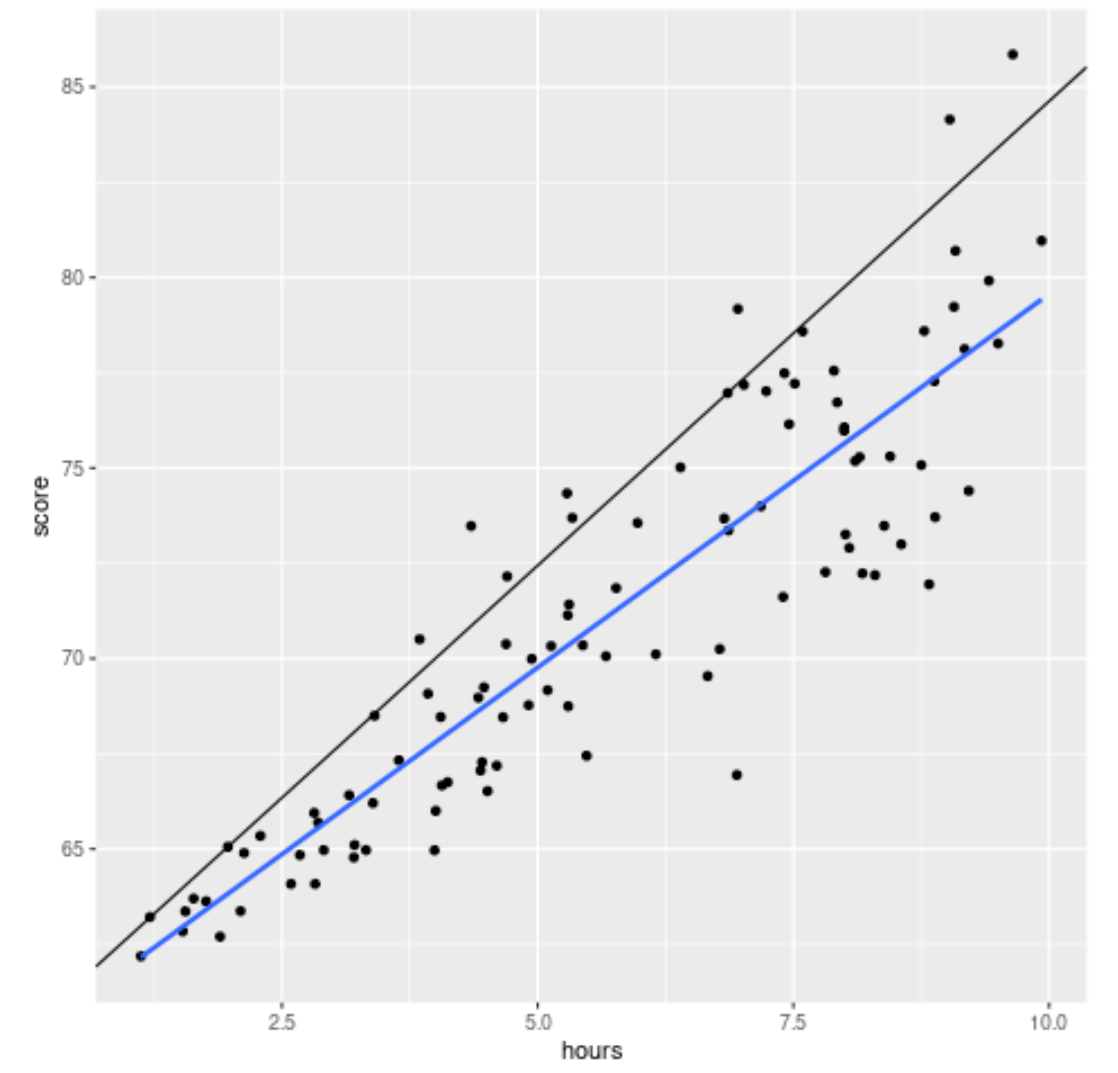
黒線は 90 パーセンタイルで調整された分位点回帰直線を表示し、青線は応答変数の平均値を推定する単純線形回帰線を表示します。
予想どおり、単純な線形回帰直線がデータ全体を貫いており、各時間レベルでの試験スコアの推定平均値が示されています。
追加リソース
次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。