R で正規性をテストする方法 (4 つの方法)
多くの統計テストは、データセットが正規分布していることを前提としています。
R でこの仮定を確認するには、次の 4 つの一般的な方法があります。
1. (視覚的方法) ヒストグラムを作成します。
- ヒストグラムがほぼ「ベル」型の場合、データは正規分布していると見なされます。
2. (視覚的方法) QQ プロットを作成します。
- プロット上の点がほぼ直線の対角線に沿って配置されている場合、データは正規分布しているとみなされます。
3. (正式な統計検定) Shapiro-Wilk 検定を実行します。
- 検定の p 値が α = 0.05 より大きい場合、データは正規分布しているとみなされます。
4. (正式な統計検定) コルモゴロフ・スミルノフ検定を実行します。
- 検定の p 値が α = 0.05 より大きい場合、データは正規分布しているとみなされます。
次の例は、これらの各メソッドを実際に使用する方法を示しています。
方法 1: ヒストグラムを作成する
次のコードは、R で正規分布データセットと非正規分布データセットのヒストグラムを作成する方法を示しています。
#make this example reproducible
set. seeds (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#define plotting region
by(mfrow=c(1,2))
#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ')
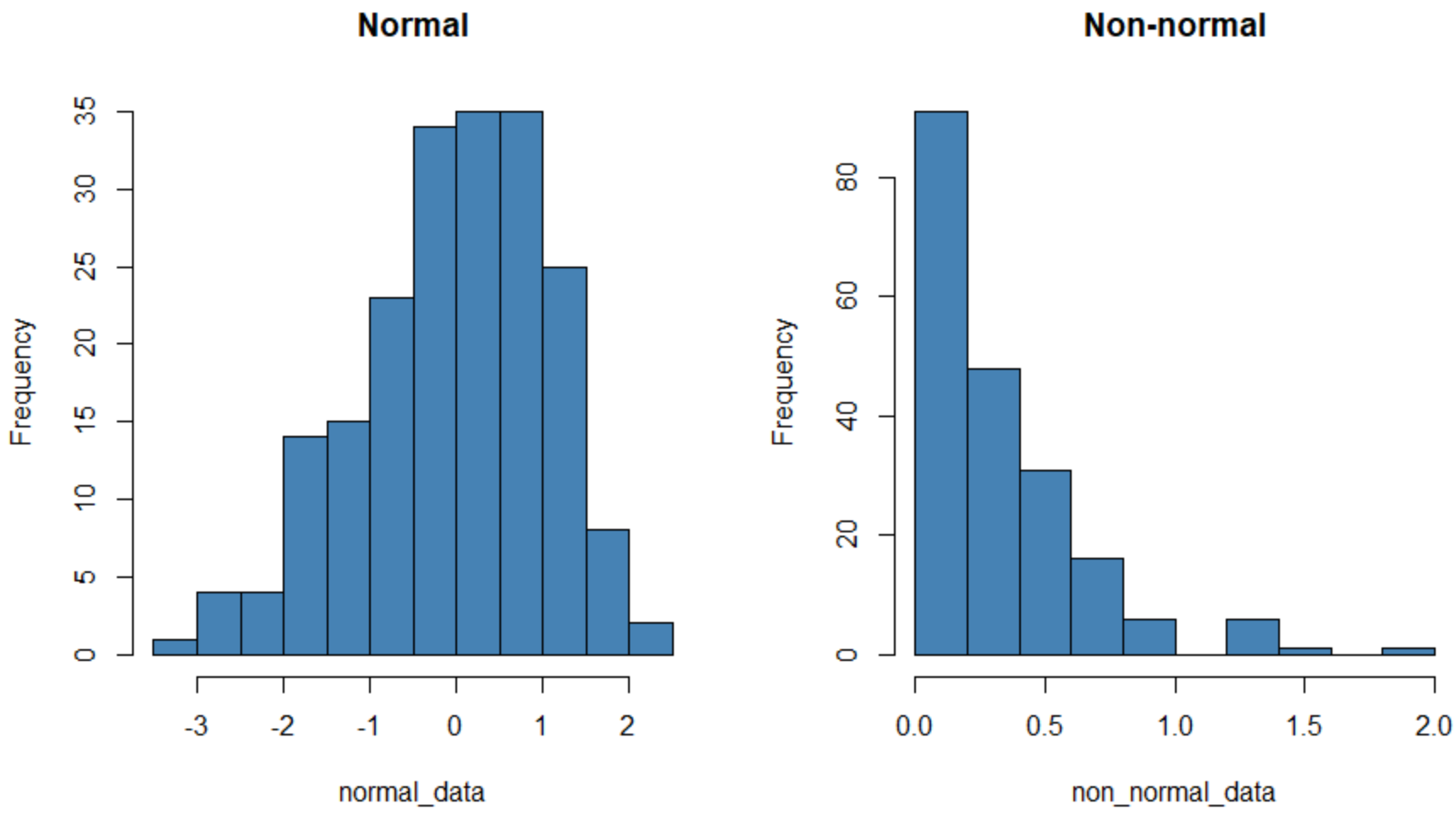
左側のヒストグラムは正規分布している (ほぼ「ベル」型) データ セットを示し、右側のヒストグラムは正規分布していないデータ セットを示しています。
方法 2: QQ プロットを作成する
次のコードは、R で正規分布データセットと非正規分布データセットの QQ プロットを作成する方法を示しています。
#make this example reproducible
set. seeds (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#define plotting region
by(mfrow=c(1,2))
#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)
qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)
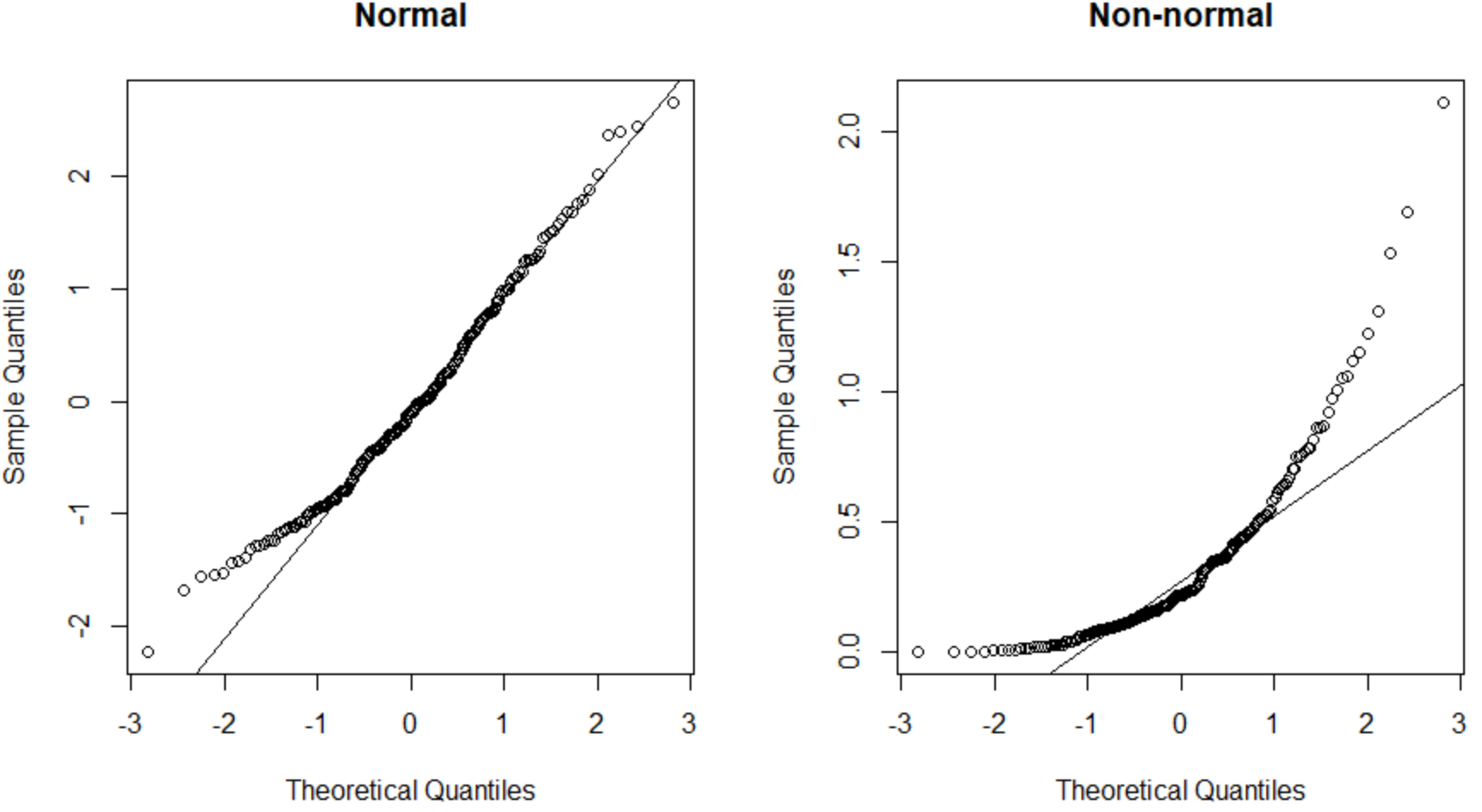
左側の QQ プロットは正規分布するデータ セット (点は直線の対角線に沿って配置されます) を示し、右側の QQ プロットは正規分布しないデータ セットを示します。
方法 3: シャピロ-ウィルク テストを実行する
次のコードは、R の正規分布データセットと非正規分布データセットに対して Shapiro-Wilk テストを実行する方法を示しています。
#make this example reproducible
set. seeds (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#perform shapiro-wilk test
shapiro. test (normal_data)
Shapiro-Wilk normality test
data: normal_data
W = 0.99248, p-value = 0.3952
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#perform shapiro-wilk test
shapiro. test (non_normal_data)
Shapiro-Wilk normality test
data: non_normal_data
W = 0.84153, p-value = 1.698e-13
最初の検定の p 値は 0.05 以上で、データが正規分布していることを示しています。
2 番目の検定の p 値は0.05 未満で、データが正規分布していないことを示しています。
方法 4: コルモゴロフ・スミルノフ検定を実行する
次のコードは、R の正規分布データセットと非正規分布データセットに対してコルモゴロフ・スミルノフ検定を実行する方法を示しています。
#make this example reproducible
set. seeds (0)
#create data that follows a normal distribution
normal_data <- rnorm(200)
#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')
One-sample Kolmogorov–Smirnov test
data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided
#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)
#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ')
One-sample Kolmogorov–Smirnov test
data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided
最初の検定の p 値は 0.05 以上で、データが正規分布していることを示しています。
2 番目の検定の p 値は0.05 未満で、データが正規分布していないことを示しています。
非正規データの扱い方
特定のデータセットが正規分布していない場合、多くの場合、次のいずれかの変換を実行して、より正規分布にすることができます。
1. 対数変換: x の値をlog(x)に変換します。
2. 平方根変換: x の値を√xに変換します。
3. 立方根変換: x の値をx 1/3に変換します。
これらの変換を実行すると、データセットは通常、より正規分布になります。
R でこれらの変換を実行する方法については、 このチュートリアルを読んでください。
追加リソース
R でヒストグラムを作成する方法
R で QQ プロットを作成して解釈する方法
R で Shapiro-Wilk テストを実行する方法
R でコルモゴロフ・スミルノフ検定を実行する方法