R での線形判別分析 (ステップバイステップ)
線形判別分析は、一連の予測子変数があり、 応答変数を2 つ以上のクラスに分類する場合に使用できる方法です。
このチュートリアルでは、R で線形判別分析を実行する方法の例を段階的に説明します。
ステップ 1: 必要なライブラリをロードする
まず、この例に必要なライブラリをロードします。
library (MASS)
library (ggplot2)
ステップ 2: データをロードする
この例では、R に組み込まれているirisデータセットを使用します。次のコードは、このデータセットをロードして表示する方法を示しています。
#attach iris dataset to make it easy to work with attach(iris) #view structure of dataset str(iris) 'data.frame': 150 obs. of 5 variables: $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ... $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ... $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ... $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ... $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...
データセットには 5 つの変数と合計 150 の観測値が含まれていることがわかります。
この例では、特定の花がどの種に属するかを分類するための線形判別分析モデルを構築します。
モデルでは次の予測子変数を使用します。
- がく片の長さ
- がく片の幅
- 花びらの長さ
- 花びらの幅
そして、それらを使用して、次の 3 つの潜在的なクラスをサポートする種の応答変数を予測します。
- セトサ
- 癜風
- バージニア州
ステップ 3: データをスケールする
線形判別分析の重要な前提の 1 つは、各予測変数が同じ分散を持つということです。この仮定が満たされていることを確認する簡単な方法は、平均が 0、標準偏差が 1 になるように各変数をスケーリングすることです。
R では、 scale()関数を使用してこれをすばやく実行できます。
#scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])
apply() 関数を使用して、各予測子変数の平均が 0 で標準偏差が 1 であることを確認できます。
#find mean of each predictor variable apply(iris[1:4], 2, mean) Sepal.Length Sepal.Width Petal.Length Petal.Width -4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 #find standard deviation of each predictor variable apply(iris[1:4], 2, sd) Sepal.Length Sepal.Width Petal.Length Petal.Width 1 1 1 1
ステップ 4: トレーニングおよびテストのサンプルを作成する
次に、データセットを、モデルをトレーニングするためのトレーニング セットと、モデルをテストするためのテスト セットに分割します。
#make this example reproducible set.seed(1) #Use 70% of dataset as training set and remaining 30% as testing set sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3)) train <- iris[sample, ] test <- iris[!sample, ]
ステップ 5: LDA モデルを調整する
次に、 MASSパッケージのlda() 関数を使用して、LDA モデルをデータに適合させます。
#fit LDA model model <- lda(Species~., data=train) #view model output model Call: lda(Species ~ ., data = train) Prior probabilities of groups: setosa versicolor virginica 0.3207547 0.3207547 0.3584906 Group means: Sepal.Length Sepal.Width Petal.Length Petal.Width setosa -1.0397484 0.8131654 -1.2891006 -1.2570316 versicolor 0.1820921 -0.6038909 0.3403524 0.2208153 virginica 0.9582674 -0.1919146 1.0389776 1.1229172 Coefficients of linear discriminants: LD1 LD2 Sepal.Length 0.7922820 0.5294210 Sepal.Width 0.5710586 0.7130743 Petal.Length -4.0762061 -2.7305131 Petal.Width -2.0602181 2.6326229 Proportion of traces: LD1 LD2 0.9921 0.0079
モデルの結果を解釈する方法は次のとおりです。
グループ事前確率:これらはトレーニング セット内の各種の割合を表します。たとえば、トレーニング セット内のすべての観測値の 35.8% は、 virginica種に関するものでした。
グループ平均:これらは、種ごとの各予測変数の平均値を表示します。
線形判別係数: LDA モデルの決定ルールをトレーニングするために使用される予測子変数の線形結合を表示します。例えば:
- LD1: 0.792 * がく片の長さ + 0.571 * がく片の幅 – 4.076 * 花びらの長さ – 2.06 * 花びらの幅
- LD2: 0.529 * がく片の長さ + 0.713 * がく片の幅 – 2.731 * 花びらの長さ + 2.63 * 花びらの幅
トレース比率:各線形判別関数によって達成される分離のパーセンテージが表示されます。
ステップ 6: モデルを使用して予測を行う
トレーニング データを使用してモデルを適合させたら、それを使用してテスト データの予測を行うことができます。
#use LDA model to make predictions on test data predicted <- predict (model, test) names(predicted) [1] "class" "posterior" "x"
これにより、3 つの変数を含むリストが返されます。
- class:予測されたクラス
- 事後確率:観測値が各クラスに属する事後確率
- x:線形判別式
テスト データセットの最初の 6 つの観測値に対するこれらの各結果をすぐに視覚化できます。
#view predicted class for first six observations in test set head(predicted$class) [1] setosa setosa setosa setosa setosa setosa Levels: setosa versicolor virginica #view posterior probabilities for first six observations in test set head(predicted$posterior) setosa versicolor virginica 4 1 2.425563e-17 1.341984e-35 6 1 1.400976e-21 4.482684e-40 7 1 3.345770e-19 1.511748e-37 15 1 6.389105e-31 7.361660e-53 17 1 1.193282e-25 2.238696e-45 18 1 6.445594e-22 4.894053e-41 #view linear discriminants for first six observations in test set head(predicted$x) LD1 LD2 4 7.150360 -0.7177382 6 7.961538 1.4839408 7 7.504033 0.2731178 15 10.170378 1.9859027 17 8.885168 2.1026494 18 8.113443 0.7563902
次のコードを使用すると、LDA モデルが種を正しく予測した観測値の割合を確認できます。
#find accuracy of model
mean(predicted$class==test$Species)
[1] 1
このモデルは、テスト データセット内の観測値の100%について種を正しく予測したことがわかりました。
現実の世界では、LDA モデルが各クラスの結果を正確に予測することはほとんどありませんが、この虹彩データセットは、機械学習アルゴリズムが非常にうまく機能する傾向にある方法で単純に構築されています。
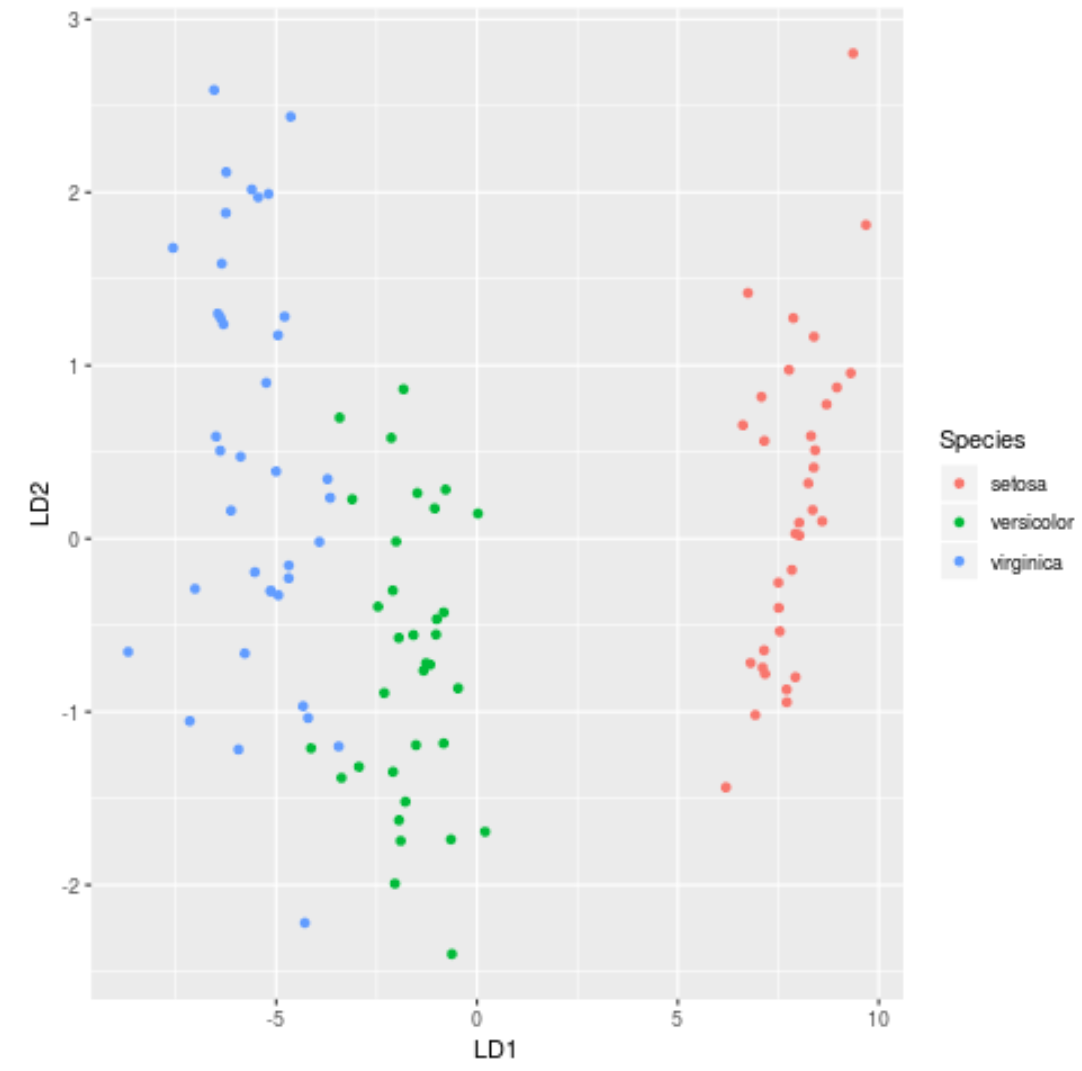
ステップ 7: 結果を視覚化する
最後に、LDA プロットを作成してモデルの線形判別式を視覚化し、データセット内の 3 つの異なる種をどの程度分離しているかを視覚化できます。
#define data to plot lda_plot <- cbind(train, predict(model)$x) #createplot ggplot(lda_plot, aes (LD1, LD2)) + geom_point( aes (color=Species))
このチュートリアルで使用される完全な R コードは、ここで見つけることができます。