R で ols 回帰を実行する方法 (例あり)
通常最小二乗 (OLS) 回帰は、1 つ以上の予測子変数と応答変数の間の関係を最もよく表す直線を見つけることを可能にする方法です。
この方法により、次の方程式を見つけることができます。
ŷ = b 0 + b 1 x
金:
- ŷ : 推定応答値
- b 0 : 回帰直線の原点
- b 1 : 回帰直線の傾き
この方程式は、予測子と応答変数の関係を理解するのに役立ち、予測子変数の値に基づいて応答変数の値を予測するために使用できます。
次の段階的な例は、R で OLS 回帰を実行する方法を示しています。
ステップ 1: データを作成する
この例では、15 人の生徒に対して次の 2 つの変数を含むデータセットを作成します。
- 総学習時間数
- 試験の結果
時間を予測変数として、試験スコアを応答変数として使用して、OLS 回帰を実行します。
次のコードは、R でこの偽のデータセットを作成する方法を示しています。
#create dataset df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14), score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89)) #view first six rows of dataset head(df) hours score 1 1 64 2 2 66 3 4 76 4 5 73 5 5 74 6 6 81
ステップ 2: データを視覚化する
OLS 回帰を実行する前に、散布図を作成して時間と試験スコアの関係を視覚化しましょう。
library (ggplot2) #create scatterplot ggplot(df, aes(x=hours, y=score)) + geom_point(size= 2 )
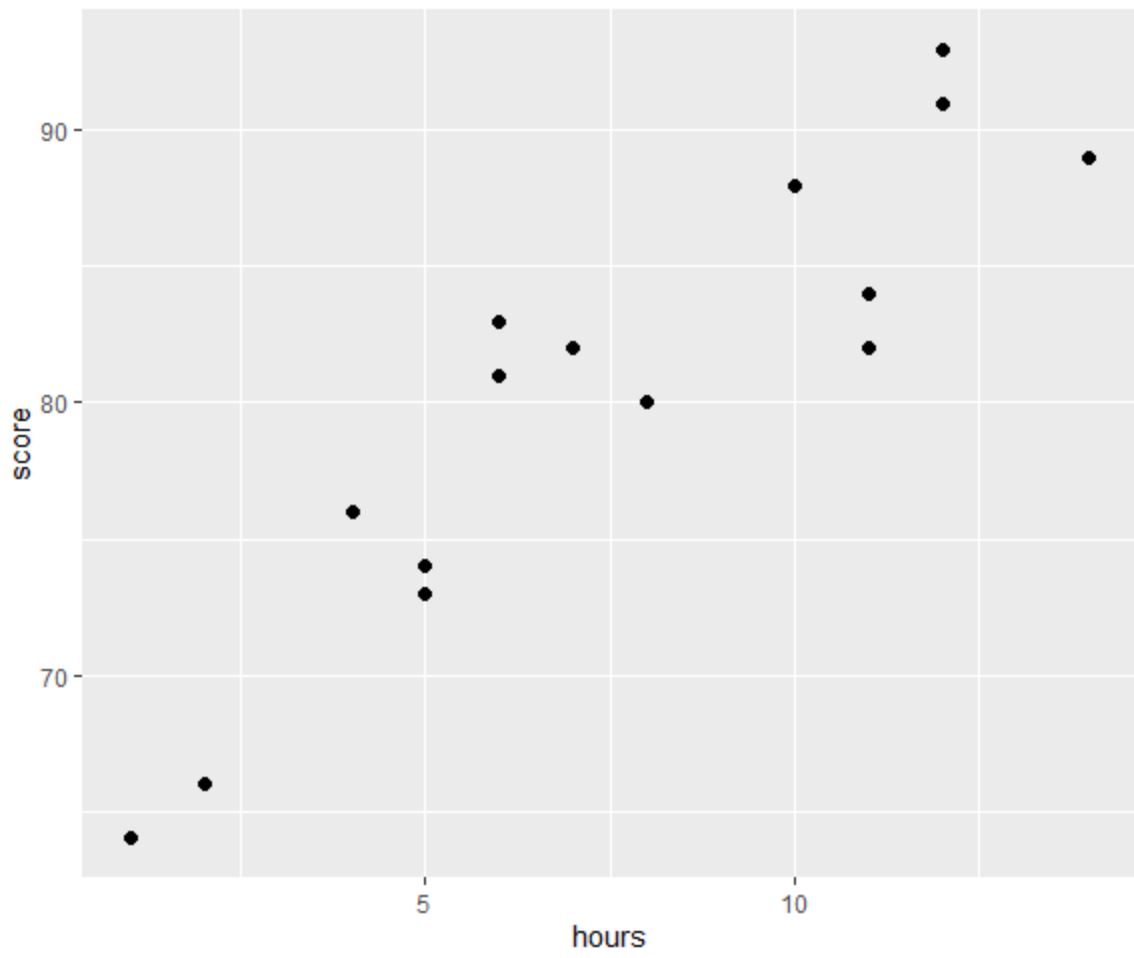
線形回帰の4 つの仮定のうちの 1 つは、予測変数と応答変数の間に線形関係があるということです。
グラフから、関係が線形であることがわかります。時間数が増加するにつれて、スコアも直線的に増加する傾向があります。
次に、箱ひげ図を作成して試験結果の分布を視覚化し、外れ値をチェックします。
注: R は、観測値が第 3 四分位より上の四分位範囲の 1.5 倍、または第 1 四分位より下の四分位範囲の 1.5 倍である場合、その観測値を外れ値として定義します。
観測値が外れ値である場合、箱ひげ図に小さな円が表示されます。
library (ggplot2) #create scatterplot ggplot(df, aes(y=score)) + geom_boxplot()
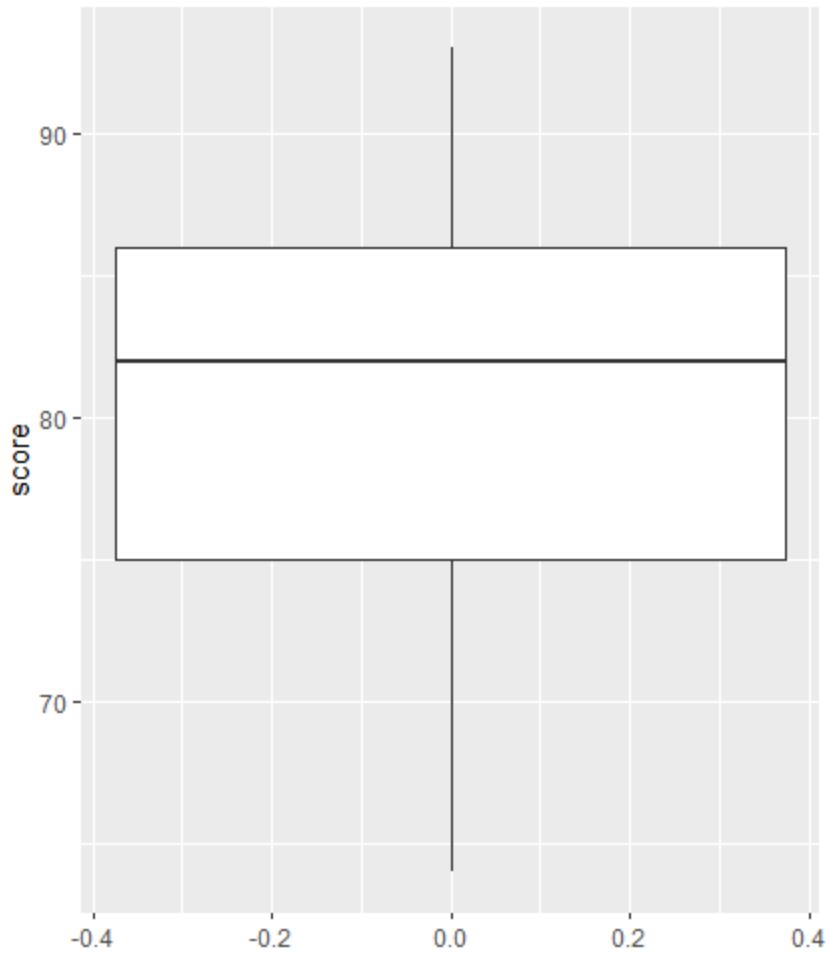
箱ひげ図には小さな円はありません。これは、データセットに外れ値がないことを意味します。
ステップ 3: OLS 回帰を実行する
次に、R のlm()関数を使用して、時間を予測変数として、スコアを応答変数として使用して、OLS 回帰を実行できます。
#fit simple linear regression model model <- lm(score~hours, data=df) #view model summary summary(model) Call: lm(formula = score ~ hours) Residuals: Min 1Q Median 3Q Max -5,140 -3,219 -1,193 2,816 5,772 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 65,334 2,106 31,023 1.41e-13 *** hours 1.982 0.248 7.995 2.25e-06 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.641 on 13 degrees of freedom Multiple R-squared: 0.831, Adjusted R-squared: 0.818 F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
モデルの概要から、近似された回帰式は次のとおりであることがわかります。
スコア = 65.334 + 1.982*(時間)
これは、学習時間が追加されるごとに、試験の平均スコアが1,982点増加することを意味します。
元の値65,334 は、 0 時間勉強した生徒の予想される試験の平均スコアを示しています。
この方程式を使用して、学生の勉強時間に基づいて予想される試験の得点を求めることもできます。
たとえば、10 時間勉強した生徒は、試験スコア85.15を達成する必要があります。
スコア = 65.334 + 1.982*(10) = 85.15
モデルの概要の残りの部分を解釈する方法は次のとおりです。
- Pr(>|t|):これはモデル係数に関連付けられた p 値です。時間の p 値 (2.25e-06) は 0.05 よりも大幅に小さいため、時間とスコアの間に統計的に有意な関連があると言えます。
- 多重 R 二乗:この数値は、試験の得点の変動のパーセンテージが勉強時間数によって説明できることを示しています。一般に、回帰モデルの R 二乗値が大きいほど、予測変数は応答変数の値をより適切に予測します。この場合、スコアの変動の83.1%は勉強時間によって説明できます。
- 残差標準誤差:これは、観測値と回帰直線の間の平均距離です。この値が低いほど、回帰直線は観察されたデータとより一致することができます。この場合、試験で観察された平均スコアは、回帰直線によって予測されたスコアから3,641ポイント外れています。
- F 統計量と p 値: F 統計量 ( 63.91 ) と対応する p 値 ( 2.253e-06 ) は、回帰モデルの全体的な有意性、つまりモデル内の予測子変数が変動を説明するのに役立つかどうかを示します。 。応答変数に。この例の p 値は 0.05 未満であるため、モデルは統計的に有意であり、時間はスコアの変動を説明するのに役立つと考えられます。
ステップ 4: 残差プロットを作成する
最後に、等分散性と正規性の仮定を確認するために残差プロットを作成する必要があります。
等分散性の仮定は、回帰モデルの残差が予測変数の各レベルでほぼ等しい分散を持つということです。
この仮定が満たされていることを確認するには、残差と近似値のプロットを作成します。
X 軸は近似値を表示し、Y 軸は残差を表示します。残差がゼロ値の周囲でグラフ全体にランダムかつ均一に分布しているように見える限り、等分散性に違反していないと仮定できます。
#define residuals res <- resid(model) #produce residual vs. fitted plot plot(fitted(model), res) #add a horizontal line at 0 abline(0,0)
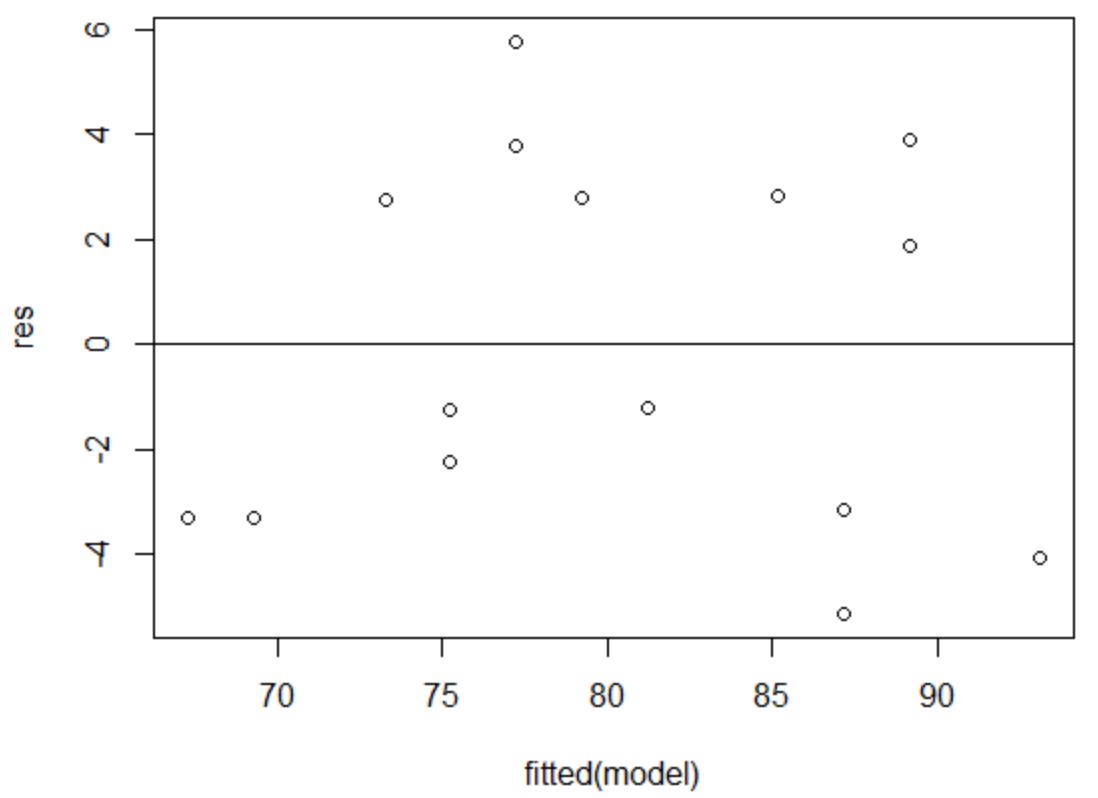
残差はゼロの周りにランダムに分散しているように見え、目立ったパターンを示さないため、この仮定は満たされます。
正規性の仮定は、回帰モデルの残差がほぼ正規分布していることを示します。
この仮定が満たされているかどうかを確認するには、 QQ プロットを作成します。プロット ポイントが 45 度の角度を形成するほぼ直線に沿って配置されている場合、データは正規分布しています。
#create QQ plot for residuals qqnorm(res) #add a straight diagonal line to the plot qqline(res)
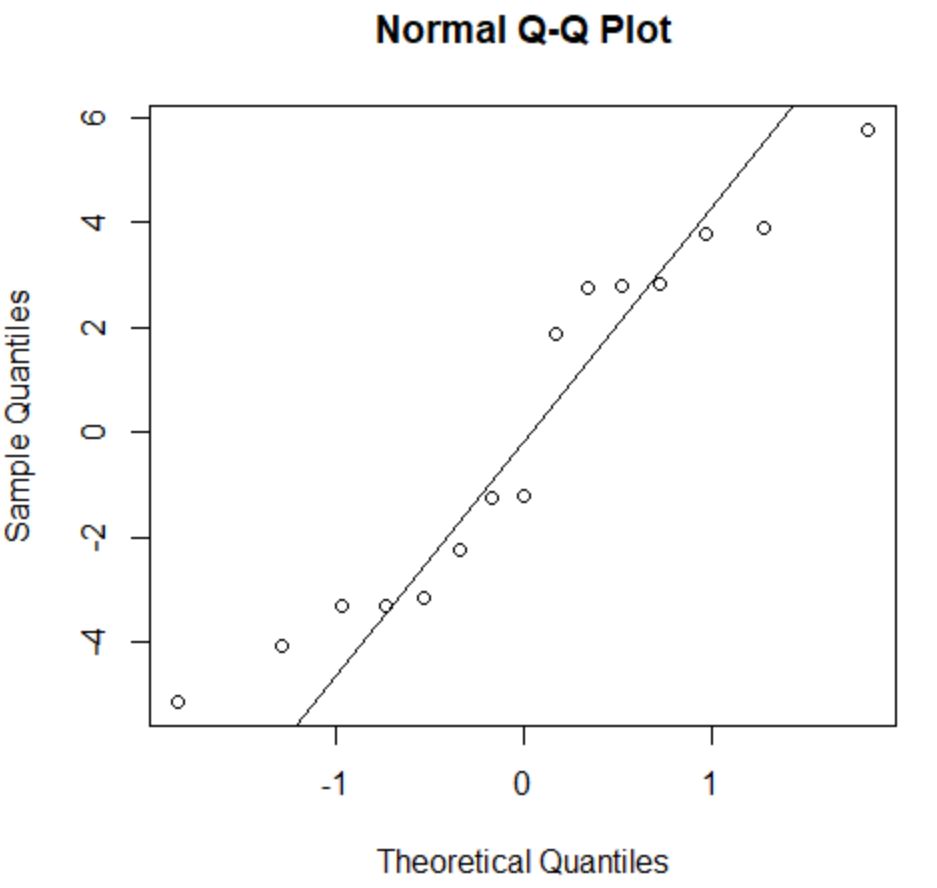
残差は 45 度の線からわずかに逸脱していますが、重大な懸念を引き起こすほどではありません。正規性の仮定が満たされていると仮定できます。
残差は正規分布し、等分散であるため、OLS 回帰モデルの仮定が満たされていることを確認しました。
したがって、モデルの出力は信頼できます。
注: 1 つ以上の前提が満たされない場合は、データの変換を試みることができます。
追加リソース
次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。