R で中心極限定理を適用する方法 (例付き)
中心極限定理は、たとえ母集団の分布が正規でなくても、サンプルサイズが十分に大きければ標本平均の標本分布はほぼ正規になる、というものです。
中心極限定理は、標本分布が次の特性を持つことも示しています。
1.標本分布の平均は母集団分布の平均と等しくなります。
x = μ
2.標本分布の標準偏差は、母集団分布の標準偏差を標本サイズで割ったものに等しくなります。
s = σ /n
次の例は、R で中心極限定理を適用する方法を示しています。
例: R における中心極限定理の適用
カメの甲羅の幅が最小幅 2 インチ、最大幅 6 インチの一様分布に従っていると仮定します。
つまり、カメを無作為に選択し、その甲羅の幅を測定すると、幅は 2 ~ 6 インチになる可能性が高くなります。
次のコードは、2 ~ 6 インチに均等に分布した 1,000 匹のカメの甲羅幅の測定値を含むデータセットを R で作成する方法を示しています。
#make this example reproducible
set. seeds (0)
#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)
#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')
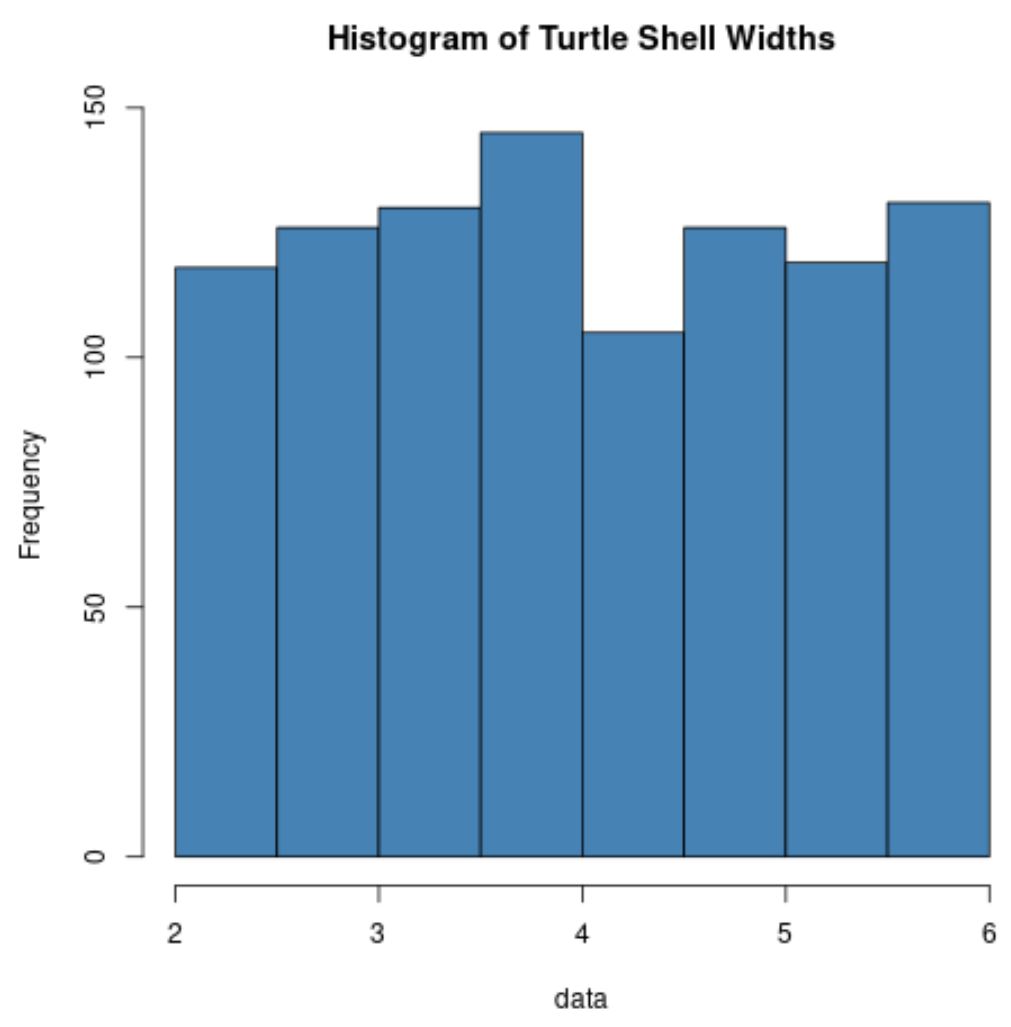
通常、カメの甲羅の幅の分布はまったく分布しないことに注意してください。
ここで、この母集団から 5 匹のカメから無作為にサンプルを繰り返し採取し、サンプルの平均値を何度も測定すると想像してください。
次のコードは、R でこのプロセスを実行し、サンプル平均の分布を視覚化するヒストグラムを作成する方法を示しています。
#create empty vector to hold sample means
sample5 <- c()
#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}
#calculate mean and standard deviation of sample means
mean(sample5)
[1] 4.008103
sd(sample5)
[1] 0.5171083
#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ')
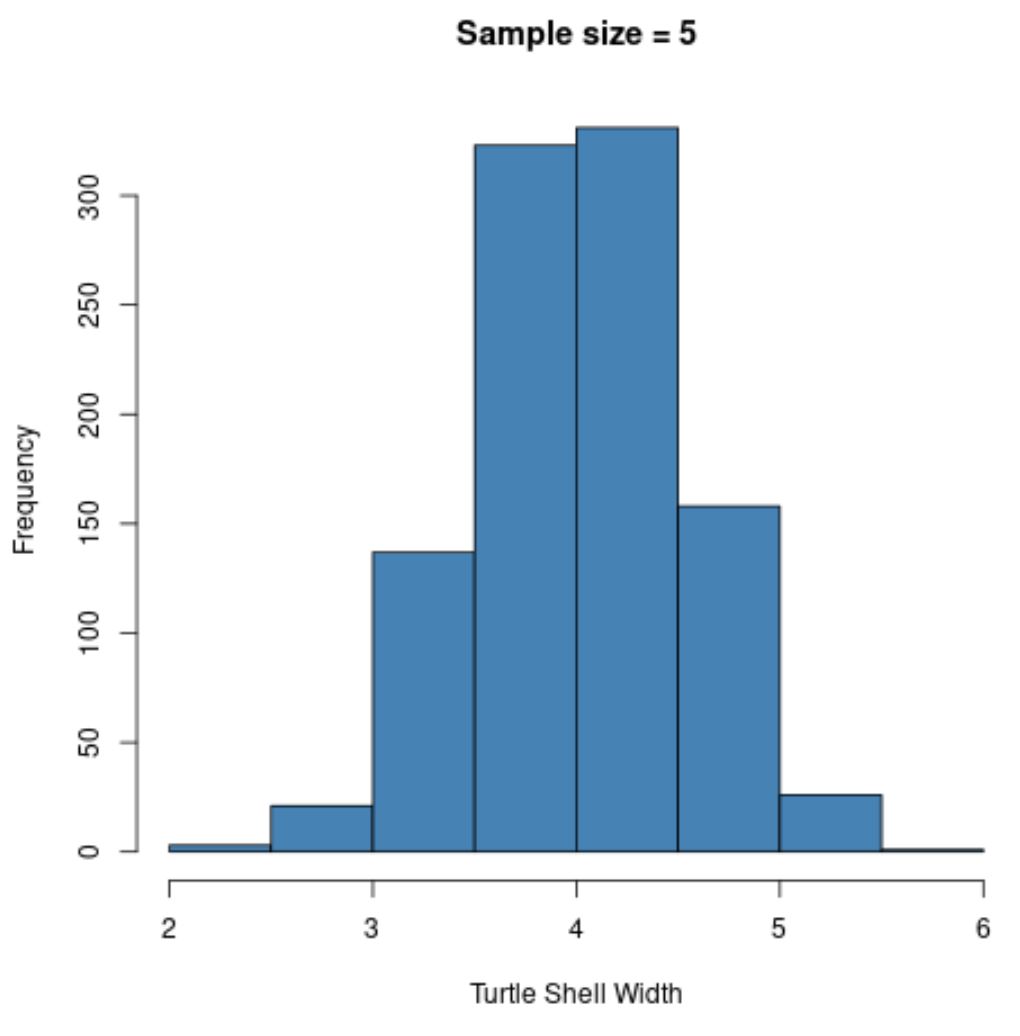
サンプルの元の分布が正規分布していなかったとしても、サンプル平均の標本分布は正規分布しているように見えることに注意してください。
この標本分布の標本平均と標本標準偏差にも注目してください。
- x̄ : 4.008
- s : 0.517
ここで、使用するサンプル サイズを n=5 から n=30 に増やし、サンプル平均のヒストグラムを再作成するとします。
#create empty vector to hold sample means
sample30 <- c()
#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}
#calculate mean and standard deviation of sample means
mean(sample30)
[1] 4.000472
sd(sample30)
[1] 0.2003791
#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ')
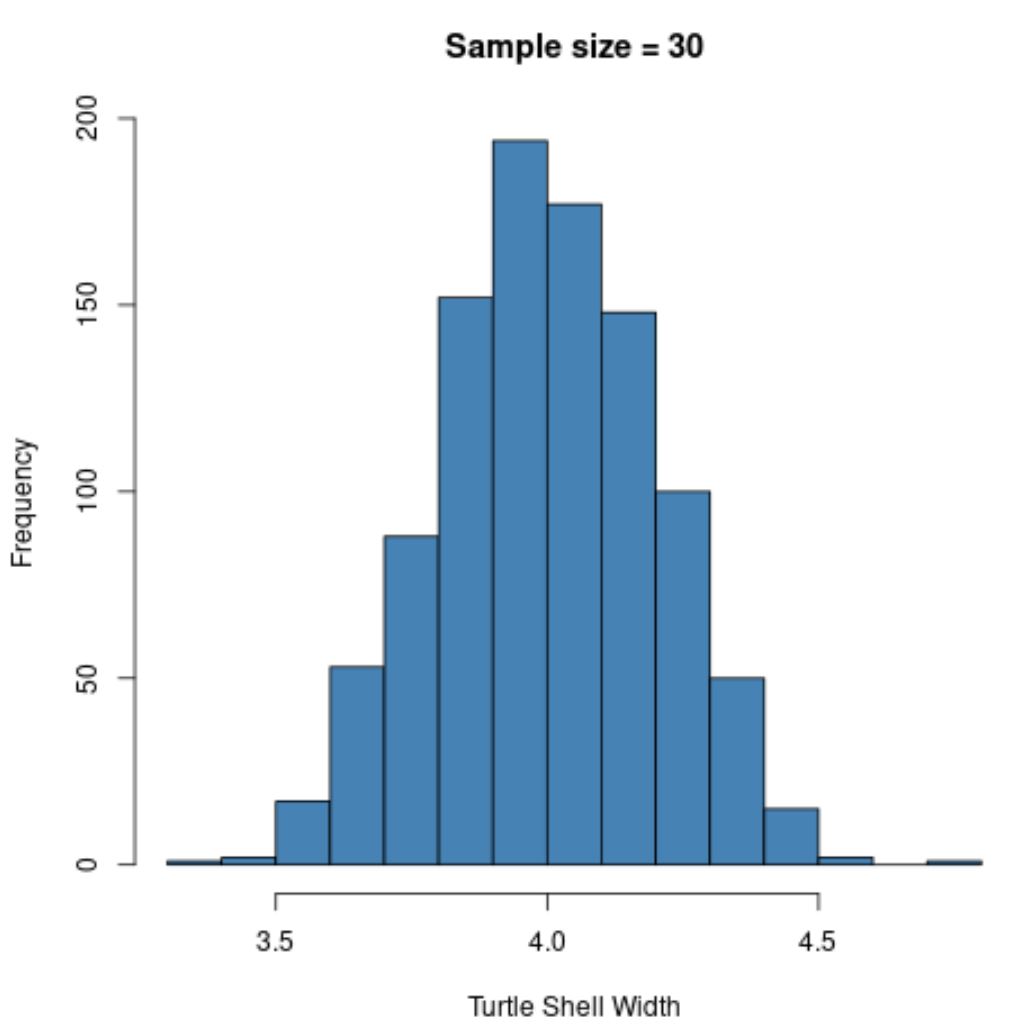
標本分布は再び正規分布になりますが、標本標準偏差はさらに小さくなります。
- 秒:0.200
これは、前の例 (n=5) と比較して大きなサンプル サイズ (n=30) を使用したため、サンプル平均の標準偏差はさらに小さくなりました。
より大きなサンプルを使用し続けると、サンプルの標準偏差がどんどん小さくなることがわかります。
これは実際の中心極限定理を示しています。
追加リソース
次のリソースは、中心極限定理に関する追加情報を提供します。