R で最小二乗法を使用する方法
最小二乗法は、特定のデータセットに最もよく適合する回帰直線を見つけるために使用できる方法です。
最小二乗法を使用して R に回帰直線を当てはめるには、 lm()関数を使用できます。
この関数は次の基本構文を使用します。
model <- lm(response ~ predictor, data=df)
次の例は、R でこの関数を使用する方法を示しています。
例: R の最小二乗法
R に、クラスの 15 人の生徒の学習時間数と対応する試験の得点を示す次のデータ フレームがあるとします。
#create data frame df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14), score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89)) #view first six rows of data frame head(df) hours score 1 1 64 2 2 66 3 4 76 4 5 73 5 5 74 6 6 81
lm()関数を使用すると、最小二乗法を使用して回帰直線をこのデータに当てはめることができます。
#use method of least squares to fit regression line model <- lm(score ~ hours, data=df) #view regression model summary summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -5,140 -3,219 -1,193 2,816 5,772 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 65,334 2,106 31,023 1.41e-13 *** hours 1.982 0.248 7.995 2.25e-06 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.641 on 13 degrees of freedom Multiple R-squared: 0.831, Adjusted R-squared: 0.818 F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06
[推定結果] 列の値から、次の近似回帰直線を書くことができます。
試験スコア = 65.334 + 1.982 (時間)
モデル内の各係数を解釈する方法は次のとおりです。
- 切片: 0 時間勉強した生徒の予想される試験スコアは65.334です。
- 時間: 学習時間がさらに 1 時間増えるごとに、予想される試験スコアは1,982増加します。
この方程式を使用して、学習時間に基づいて学生が受け取る試験の成績を推定できます。
たとえば、学生が 5 時間勉強した場合、試験のスコアは 75.244 になると推定されます。
試験スコア = 65.334 + 1.982(5) = 75.244
最後に、近似回帰直線をプロット上に重ね合わせた元のデータの散布図を作成できます。
#create scatter plot of data plot(df$hours, df$score, pch=16, col=' steelblue ') #add fitted regression line to scatter plot abline(model)
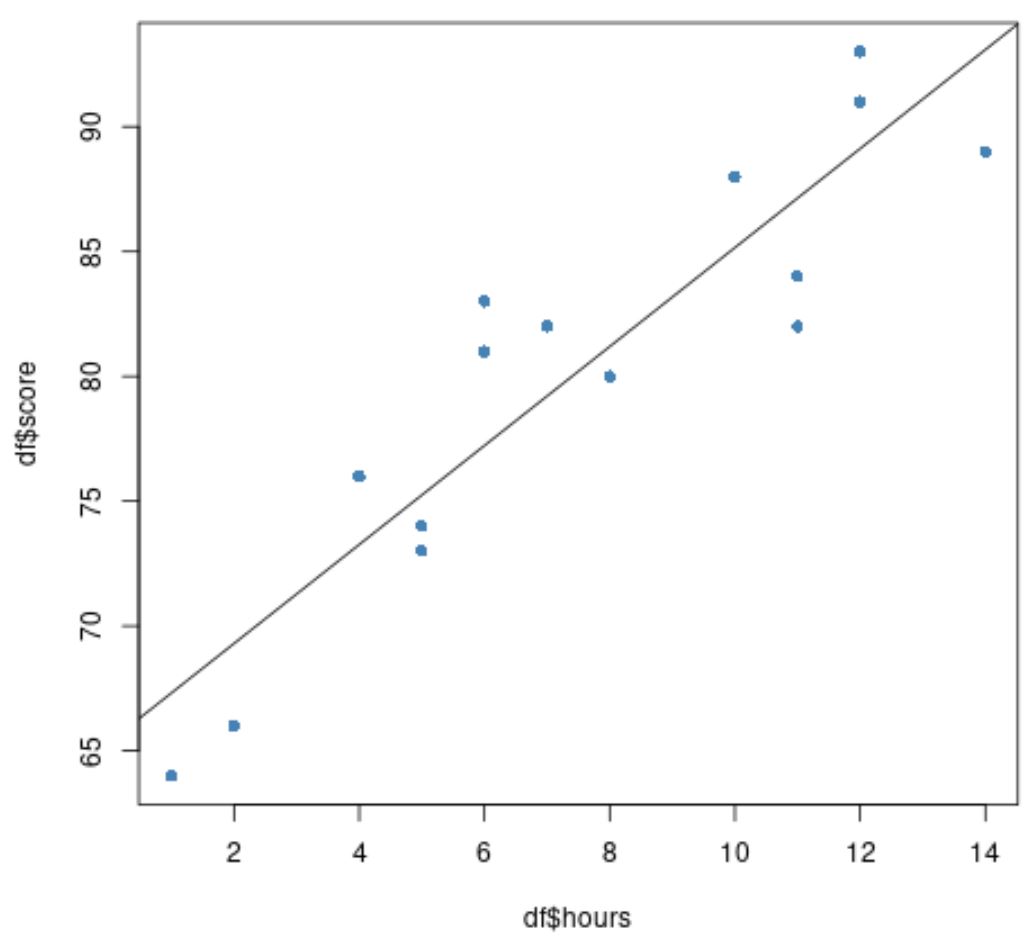
青い円はデータを表し、黒い線は近似された回帰直線を表します。
追加リソース
次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。