R で標本分布を計算する方法
標本分布は、単一母集団からの多数の無作為サンプルに基づく特定の統計量の確率分布です。
このチュートリアルでは、R でサンプリング分布を使用して次のことを行う方法について説明します。
- 標本分布を生成します。
- 標本分布を視覚化します。
- 標本分布の平均値と標準偏差を計算します。
- 標本分布に関する確率を計算します。
R で標本分布を生成する
次のコードは、R で標本分布を生成する方法を示しています。
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656
この例では、 rnorm()関数を使用して、各サンプル サイズが 20 で、平均 5.3、標準偏差 9 の正規分布から生成された 10,000 サンプルの平均を計算しました。
最初のサンプルの平均は 5.283992、2 番目のサンプルの平均は 6.304845 などであることがわかります。
標本分布を視覚化する
次のコードは、標本分布を視覚化するための単純なヒストグラムを作成する方法を示しています。
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
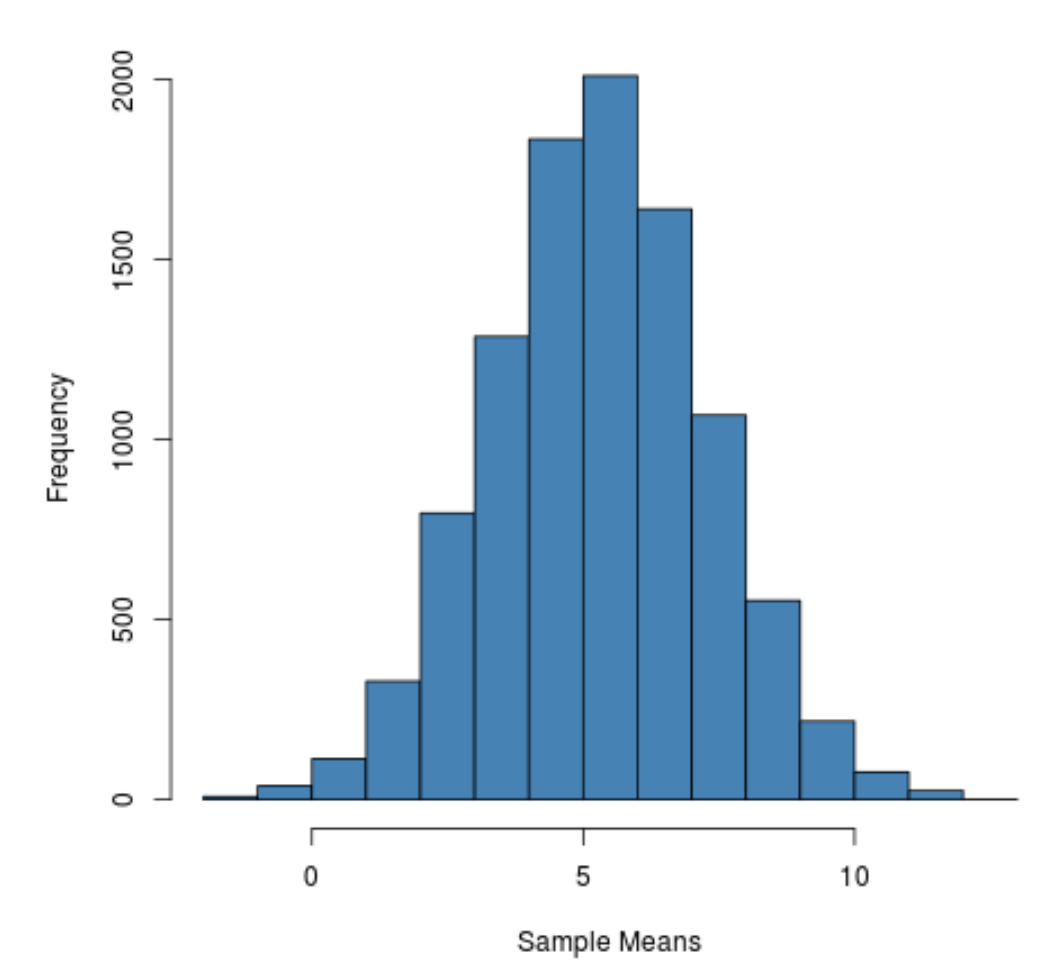
標本分布は値 5 付近にピークを持つ釣鐘型であることがわかります。
ただし、分布の裾から、一部のサンプルの平均値は 10 を超え、他のサンプルの平均値は 0 未満であることがわかります。
平均と標準偏差を求める
次のコードは、標本分布の平均値と標準偏差を計算する方法を示しています。
#mean of sampling distribution
mean(sample_means)
[1] 5.287195
#standard deviation of sampling distribution
sd(sample_means)
[1] 2.00224
理論的には、標本分布の平均値は5.3になるはずです。この例の実際のサンプル平均は5.287195で、5.3 に近いことがわかります。
そして理論的には、標本分布の標準偏差は s/√n に等しいはずで、9 / √20 = 2.012 となります。標本分布の実際の標準偏差は2.00224で、2.012 に近いことがわかります。
確率を計算する
次のコードは、母平均、母標準偏差、サンプル サイズを指定して、サンプル平均の特定の値が得られる確率を計算する方法を示しています。
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)
この特定の例では、母集団平均が 5.3、母集団標準偏差が 9、標本サイズ 20 が0.6417であることを考慮して、標本平均が 6 以下である確率を求めます。
これは、 Sampling Distribution Calculatorで計算された確率に非常に近いです。

完全なコード
この例で使用される完全な R コードを以下に示します。
#make this example reproducible
set.seed(0)
#define number of samples
n = 10000
#create empty vector of length n
sample_means = rep (NA, n)
#fill empty vector with means
for (i in 1:n){
sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}
#view first six sample means
head(sample_means)
#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")
#mean of sampling distribution
mean(sample_means)
#standard deviation of sampling distribution
sd(sample_means)
#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)