R で二変量解析を実行する方法 (例付き)
二変量分析という用語は、2 つの変数の分析を指します。接頭辞「bi」は「2」を意味するので、これを覚えておくとよいでしょう。
二変量解析の目標は、2 つの変数間の関係を理解することです。
二変量解析を実行するには、次の 3 つの一般的な方法があります。
1.点群
2.相関係数
3.単純な線形回帰
次の例は、2 つの変数(1)勉強に費やした時間、および(2) 20 人の異なる学生が獲得したテストのスコアに関する情報を含む次のデータ セットを使用して、これらのタイプの二変量分析を実行する方法を示しています。
#create data frame df <- data. frame (hours=c(1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 5, 5, 6, 6, 6, 7, 8), score=c(75, 66, 68, 74, 78, 72, 85, 82, 90, 82, 80, 88, 85, 90, 92, 94, 94, 88, 91, 96)) #view first six rows of data frame head(df) hours score 1 1 75 2 1 66 3 1 68 4 2 74 5 2 78 6 2 72
1. 点群
次の構文を使用して、R で学習時間と試験の成績の散布図を作成できます。
#create scatterplot of hours studied vs. exam score plot(df$hours, df$score, pch= 16 , col=' steelblue ', main=' Hours Studied vs. Exam Score ', xlab=' Hours Studied ', ylab=' Exam Score ')
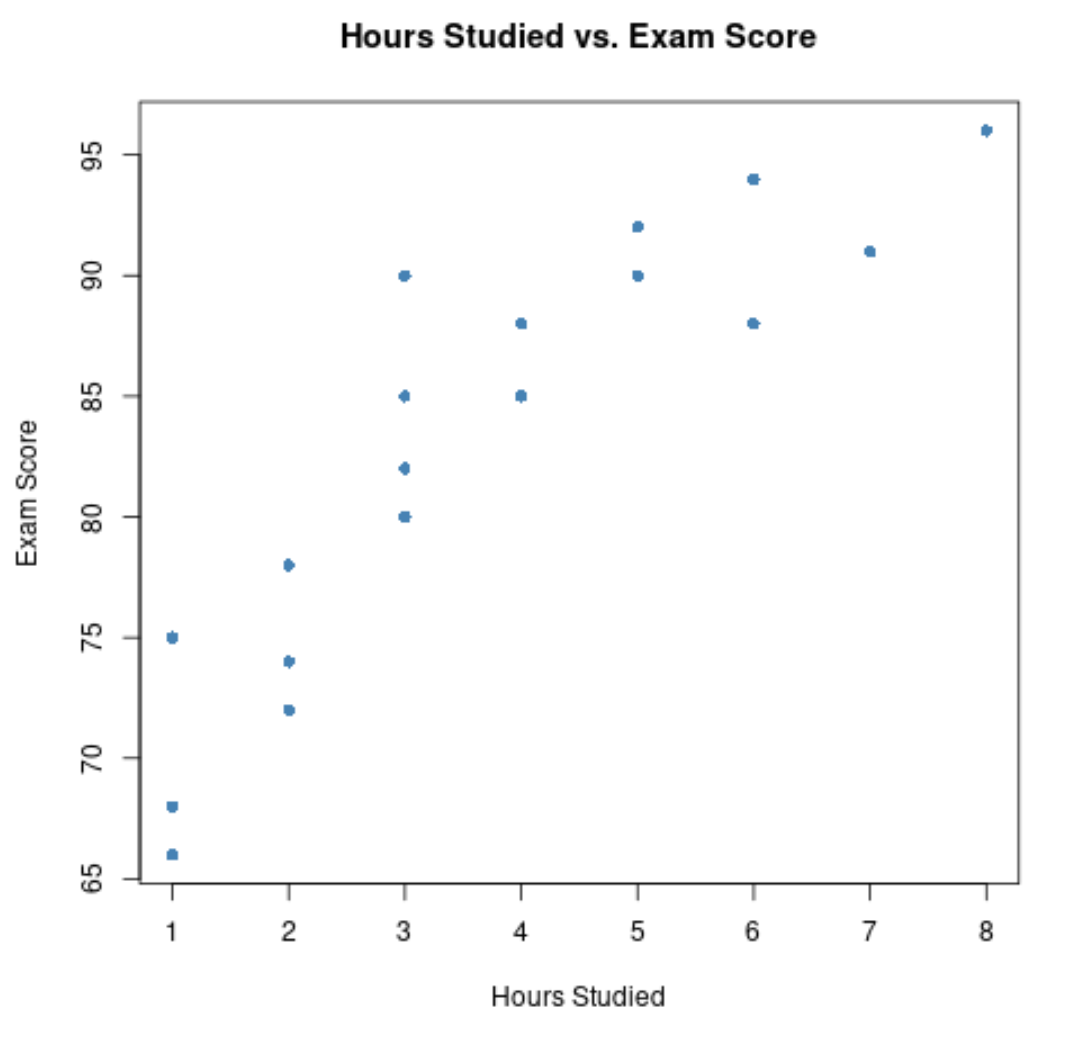
X 軸は学習時間を示し、Y 軸は試験で獲得した成績を示します。
グラフは、2 つの変数の間に正の関係があることを示しています。学習時間数が増加するにつれて、試験のスコアも増加する傾向があります。
2. 相関係数
ピアソン相関係数は、2 つの変数間の線形関係を定量化する方法です。
R のcor()関数を使用して、2 つの変数間のピアソン相関係数を計算できます。
#calculate correlation between hours studied and exam score received
cor(df$hours, df$score)
[1] 0.891306
相関係数は0.891であることがわかります。
この値は 1 に近く、学習時間と試験の成績の間に強い正の相関があることを示しています。
3. 単純な線形回帰
単純線形回帰は、一連のデータに最もよく「適合」する直線の方程式を見つけるために使用できる統計手法であり、これを使用して 2 つの変数間の正確な関係を理解できます。
R のlm()関数を使用して、学習時間と受け取った試験結果に対する単純な線形回帰モデルを当てはめることができます。
#fit simple linear regression model fit <- lm(score ~ hours, data=df) #view summary of model summary(fit) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -6,920 -3,927 1,309 1,903 9,385 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 69.0734 1.9651 35.15 < 2nd-16 *** hours 3.8471 0.4613 8.34 1.35e-07 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 4.171 on 18 degrees of freedom Multiple R-squared: 0.7944, Adjusted R-squared: 0.783 F-statistic: 69.56 on 1 and 18 DF, p-value: 1.347e-07
近似された回帰式は次のようになります。
試験スコア = 69.0734 + 3.8471*(勉強時間)
これは、学習時間が追加されるごとに、試験スコアが平均3.8471増加することを示しています。
また、適合回帰式を使用して、合計学習時間数に基づいて生徒が受け取るスコアを予測することもできます。
たとえば、3 時間勉強した生徒は81.6147のスコアを取得する必要があります。
- 試験スコア = 69.0734 + 3.8471*(勉強時間)
- 試験のスコア = 69.0734 + 3.8471*(3)
- 試験結果 = 81.6147
追加リソース
次のチュートリアルでは、二変量解析に関する追加情報を提供します。