R でマシューズの相関係数を計算する方法
マシューズ相関係数(MCC) は、分類モデルのパフォーマンスを評価するために使用できる指標です。
次のように計算されます。
MCC = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)
金:
- TP : 真陽性者数
- TN : 真陰性の数
- FP : 誤検知数
- FN : 偽陰性の数
このメトリクスは、2 つのクラスのバランスが崩れている場合、つまり、一方のクラスが他方のクラスよりも多く表示される場合に特に役立ちます。
MCC の値は -1 ~ 1 です。ここで、
- -1 は、予測されたクラスと実際のクラスがまったく一致しないことを示します
- 0 は完全にランダムな推測を意味します
- 1 は、予測されたクラスと実際のクラスが完全に一致していることを示します
たとえば、スポーツ アナリストがロジスティック回帰モデルを使用して、400 人の大学バスケットボール選手が NBA にドラフトされるかどうかを予測するとします。
次の混同行列は、モデルによって行われた予測を要約したものです。
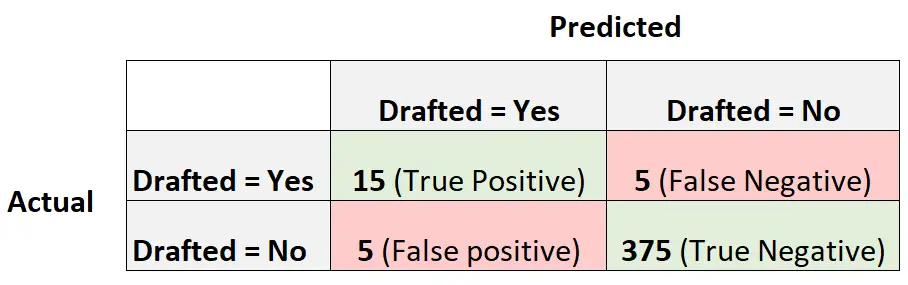
モデルの MCC を計算するには、次の式を使用できます。
- MCC = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)
- MCC = (15*375-5*5) / √ (15+5)(15+5)(375+5)(375+5)
- MCC = 0.7368
マシューズの相関係数は0.7368であることがわかります。
この値は 1 にやや近く、モデルが選手がドラフトされるかどうかを適切に予測していることを示しています。
次の例は、R のmltoolsパッケージのmcc()関数を使用して、この特定のシナリオの MCC を計算する方法を示しています。
例: R でのマシューズ相関係数の計算
次のコードは、予測クラスのベクトルと実際のクラスのベクトルを定義し、 mltoolsパッケージのmcc()関数を使用してマシューズ相関係数を計算する方法を示しています。
library (mltools) #define vector of actual classes actual <- rep (c(1, 0), times =c(20, 380)) #define vector of predicted classes preds <- rep (c(1, 0, 1, 0), times =c(15, 5, 5, 375)) #calculate Matthews correlation coefficient mcc(preds, actual) [1] 0.7368421
マシューズの相関係数は0.7368です。
これは、以前に手動で計算した値と一致します。
混同行列のマシューズ相関係数を計算する場合は、次のようにconfusionM引数を使用できます。
library (mltools) #create confusion matrix conf_matrix <- matrix(c(15, 5, 5, 375), nrow= 2 ) #view confusion matrix conf_matrix [,1] [,2] [1,] 15 5 [2,] 5,375 #calculate Matthews correlation coefficient for confusion matrix mcc(confusionM = conf_matrix) [1] 0.7368421
ここでも、マシューズの相関係数は0.7368 です。
追加リソース
次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。
R でロジスティック回帰を実行する方法
ggplot2 を使用して ROC 曲線をプロットする方法
R で F1 スコアを計算する方法