R で通常の cdf を使用する方法 (例あり)
次のメソッドを使用して、R で通常の CDF (累積分布関数) を操作できます。
方法 1: 正規 CDF 確率を計算する
#calculate probability that random value is less than 1.96 in normal CDF pnorm(1.96) #calculate probability that random value is greater than 1.96 in normal CDF pnorm(1.96, lower.tail = FALSE )
方法 2: 正規 CDF をプロットする
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #normal plot CDF plot(x, prob, type=" l ")
次の例は、これらのメソッドを実際に使用する方法を示しています。
例 1:正規 CDF確率を計算する
次のコードは、標準正規分布で確率変数が 1.96 未満の値を取る確率を計算する方法を示しています。
#calculate probability that random value is less than 1.96 in normal CDF
pnorm(1.96)
[1] 0.9750021
標準正規分布で確率変数が 1.96 未満の値をとる確率は0.975です。
また、 lower.tail引数を使用して、確率変数が 1.96 より大きい値を取る確率を求めることもできます。
#calculate probability that random value is greater than 1.96 in normal CDF pnorm(1.96, lower.tail = FALSE ) [1] 0.0249979
そして、次の構文を使用して、確率変数が標準正規分布の 2 つの値の間の値を取る確率を見つけることができます。
#calculate probability that random value takes on value between -1.96 and 1.96
pnorm(1.96) - pnorm(-1.96)
[1] 0.9500042
標準正規分布で確率変数が -1.96 ~ 1.96 の値を取る確率は0.95です。
例 2: 標準 CDF のプロット
次のコードは、通常の CDF をプロットする方法を示しています。
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #normal plot CDF plot(x, prob, type=" l ")
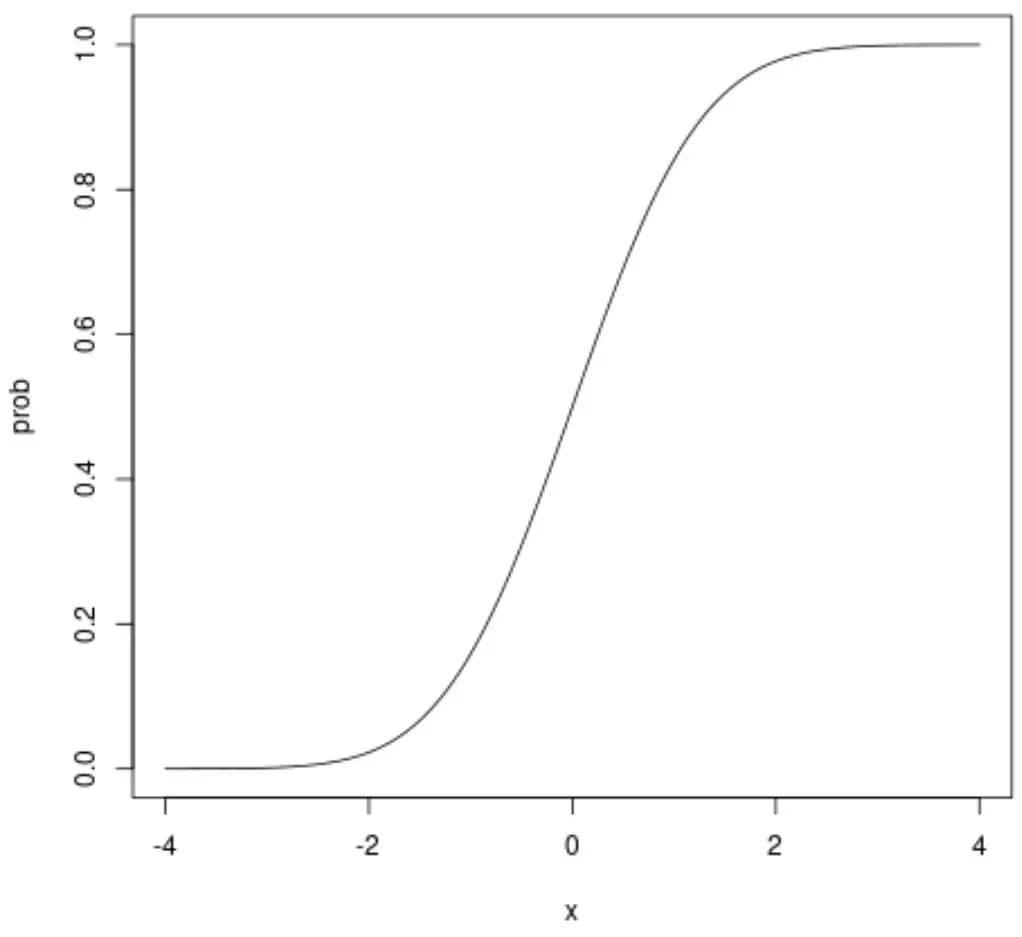
x 軸は標準正規分布に従う確率変数の値を示し、y 軸は確率変数が x 軸に示された値よりも小さい値を取る確率を示します。
たとえば、x = 1.96 を見ると、x が 1.96 未満である累積確率は約0.975 であることがわかります。
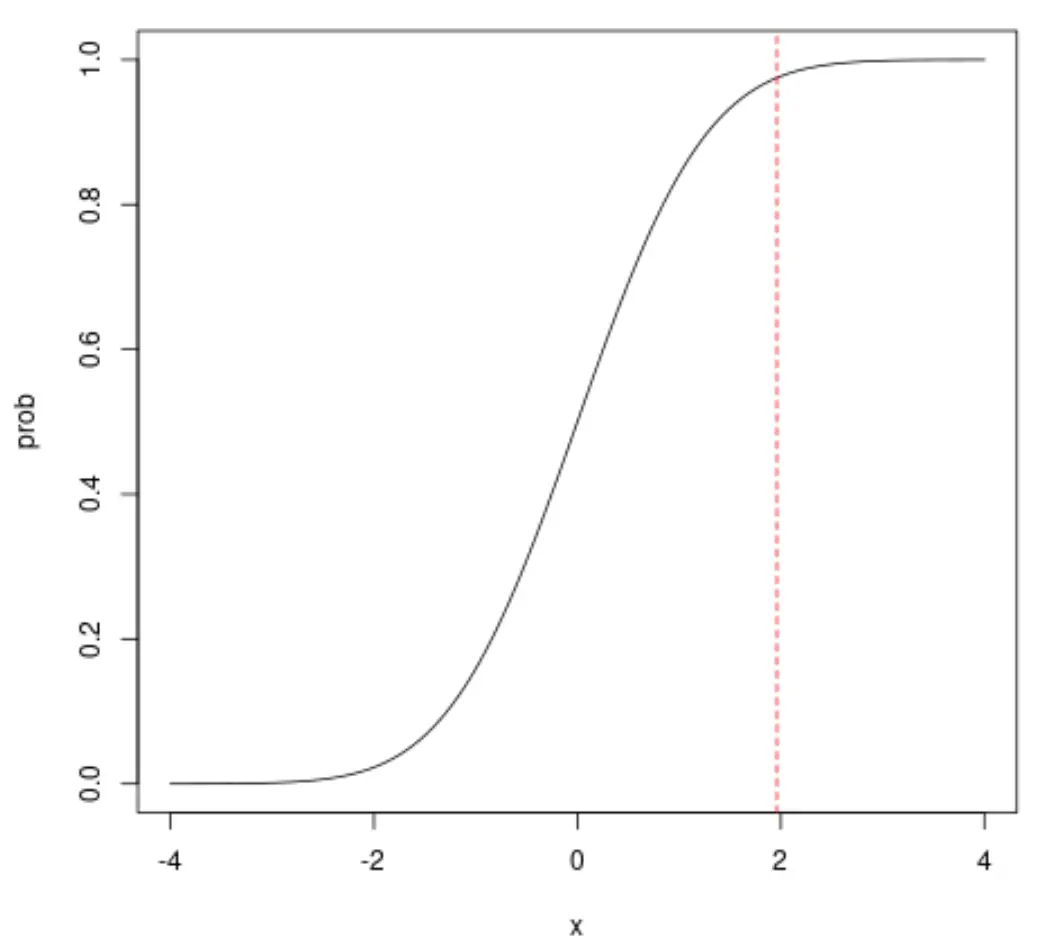
通常の CDF プロットの外観を変更することもできることに注意してください。
#define sequence of x-values x <- seq(-4, 4, .01) #calculate normal CDF probabilities prob <- pnorm(x) #normal plot CDF plot(x, prob, type=' l ', col=' blue ', lwd= 2 , main=' Normal CDF ', ylab=' Cumulative Prob ')
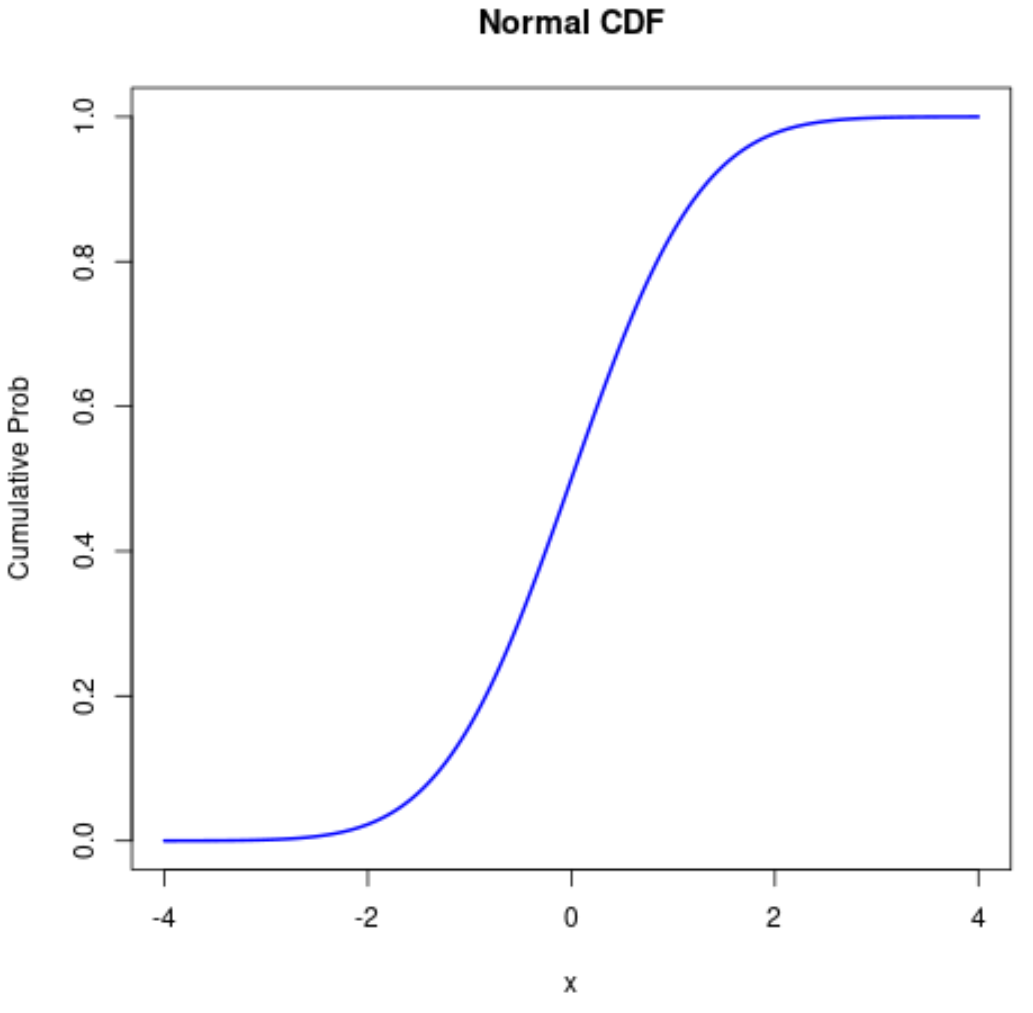
追加リソース
次のチュートリアルでは、R で他の一般的な操作を実行する方法について説明します。
R で正規分布をプロットする方法
R で Z スコアを計算する方法
R の dnorm、pnorm、qnorm、rnorm のガイド