R と r 2 乗: 違いは何ですか?

学生が統計学でよく混同する 2 つの用語は、 RとR 二乗( ^R2と書かれることが多い) です。

単純な線形回帰のコンテキストでは:

• A:予測変数 x と応答変数 y の間の相関関係。
• R ² :回帰モデルの予測変数によって説明できる応答変数の分散の割合。

そして、重線形回帰のコンテキストでは次のようになります。

• A:応答変数の観測値とモデルによって作成された応答変数の予測値の間の相関関係。
• R ² :回帰モデルの予測変数によって説明できる応答変数の分散の割合。

R ²の値は 0 ～ 1 であることに注意してください。値が 1 に近づくほど、予測変数と応答変数の間の関係が強くなります。

次の例は、単線形回帰モデルと重線形回帰モデルで R 値と R 二乗値を解釈する方法を示しています。

例 1: 単純な線形回帰

特定の数学コースの 12 人の生徒の学習時間と取得した試験の得点を示す次のデータセットがあるとします。

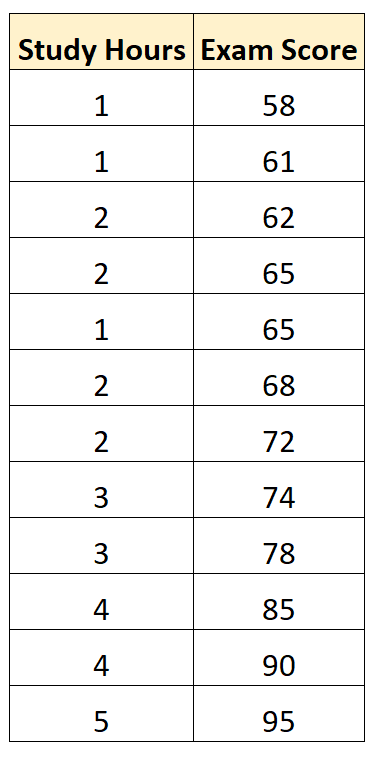
統計ソフトウェア (Excel、R、Python、SPSS など) を使用すると、「学習時間」を予測変数として、「試験の成績」を応答変数として使用する単純な線形回帰モデルを当てはめることができます。

このモデルの出力は次のとおりです。

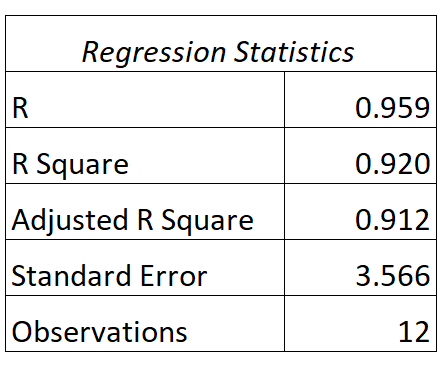
このモデルの R 値と R 2 乗値を解釈する方法は次のとおりです。

• A:勉強時間と試験のスコアの相関関係は0.959です。
• R ² : この回帰モデルの R の二乗は0.920です。これは、試験の得点の変動の 92.0% が勉強時間によって説明できることがわかります。

また、R ²値は単純に R 値の 2 乗に等しいことにも注意してください。

^R2 = R * R = 0.959 * 0.959 = 0.920

例 2: 重回帰

特定の数学コースの 12 人の生徒の学習時間、現在の生徒の成績、および試験の成績を示す次のデータセットがあるとします。

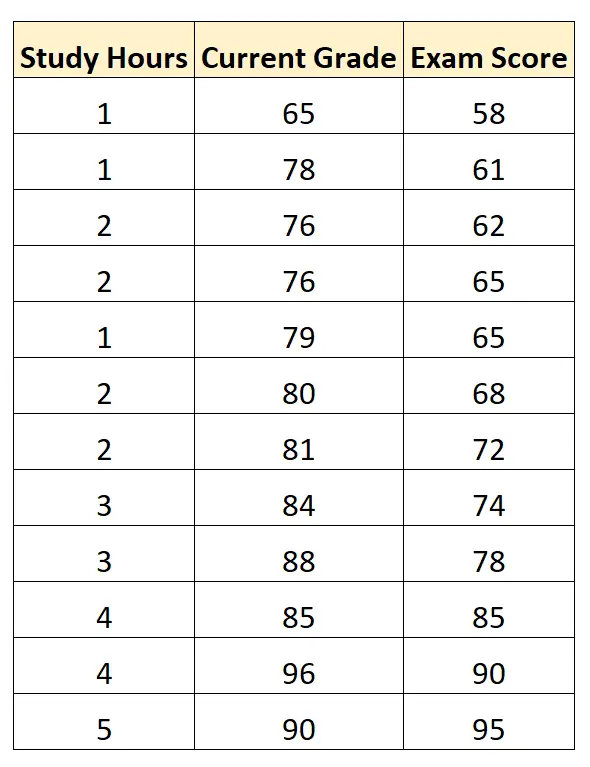
統計ソフトウェアを使用すると、「学習時間」と「現在の成績」を予測変数として、「試験の成績」を応答変数として使用して重線形回帰モデルを当てはめることができます。

このモデルの出力は次のとおりです。

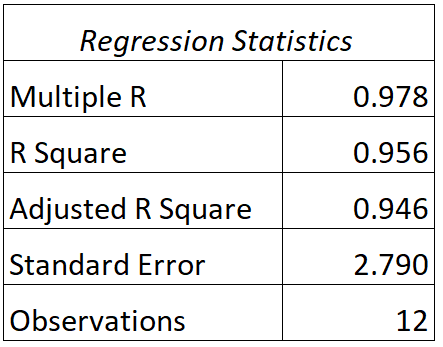
このモデルの R 値と R 2 乗値を解釈する方法は次のとおりです。

• A:実際のテスト スコアとモデルの予測テスト スコア間の相関は0.978です。
• R ² : この回帰モデルの R の二乗は0.956です。これは、試験の得点の変動の 95.6% が、学習時間数とクラス内の生徒の現在の成績によって説明できることがわかります。

また、R ²値は単純に R 値の 2 乗に等しいことにも注意してください。

^R2 = R * R = 0.978 * 0.978 = 0.956

追加リソース

適切な R 二乗値はどれくらいですか?
二乗和の優しいガイド: SST、SSR、SSE