R でスプライン回帰を実行する方法 (例あり)

スプライン回帰は、データ内のパターンが突然変化する点または「結び目」があり、 線形回帰と多項式回帰ではデータに適合するのに十分な柔軟性がない場合に使用される回帰の一種です。

次の段階的な例は、R でスプライン回帰を実行する方法を示しています。

ステップ 1: データを作成する

まず、2 つの変数を含むデータセットを R で作成し、変数間の関係を視覚化する散布図を作成しましょう。

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

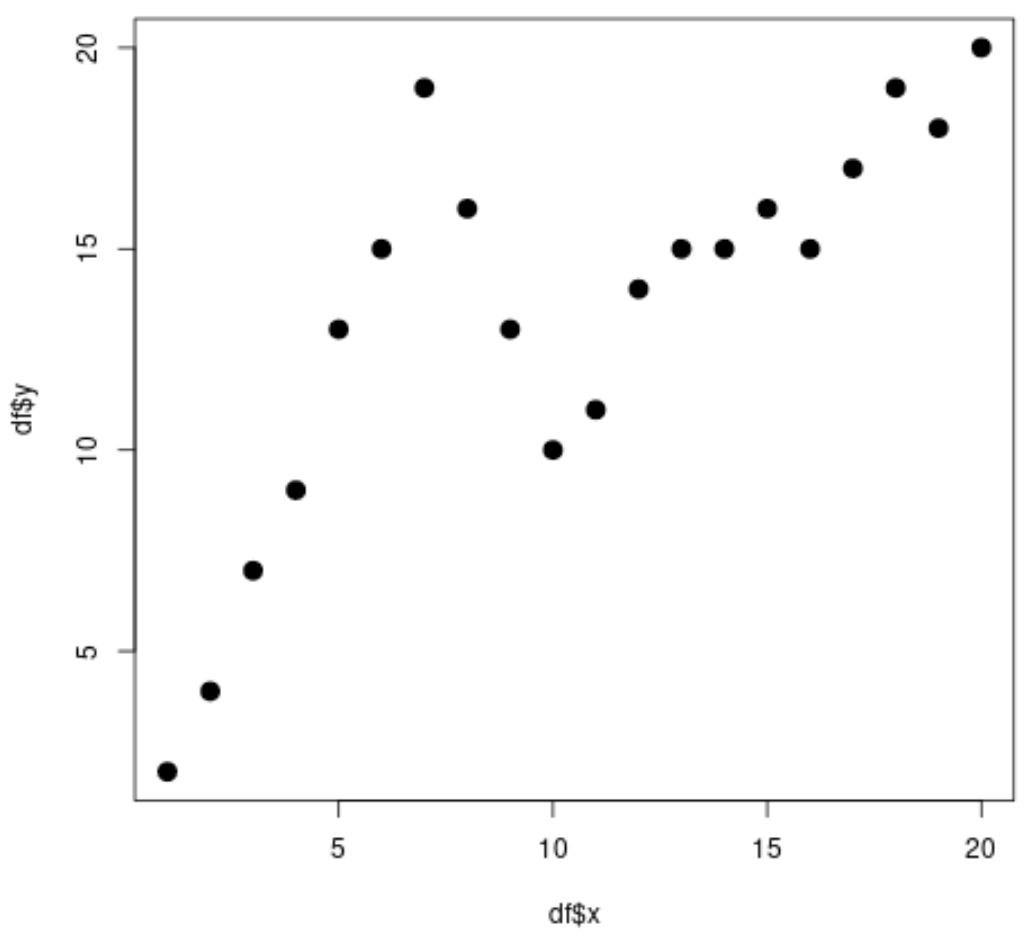
明らかに、x と y の関係は非線形であり、データ内のパターンが x=7 と x=10 で突然変化する 2 つの点または「ノード」があるように見えます。

ステップ 2: 単純な線形回帰モデルを当てはめる

次に、 lm() 関数を使用して単純な線形回帰モデルをこのデータセットに近似し、回帰直線を散布図上にプロットします。

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

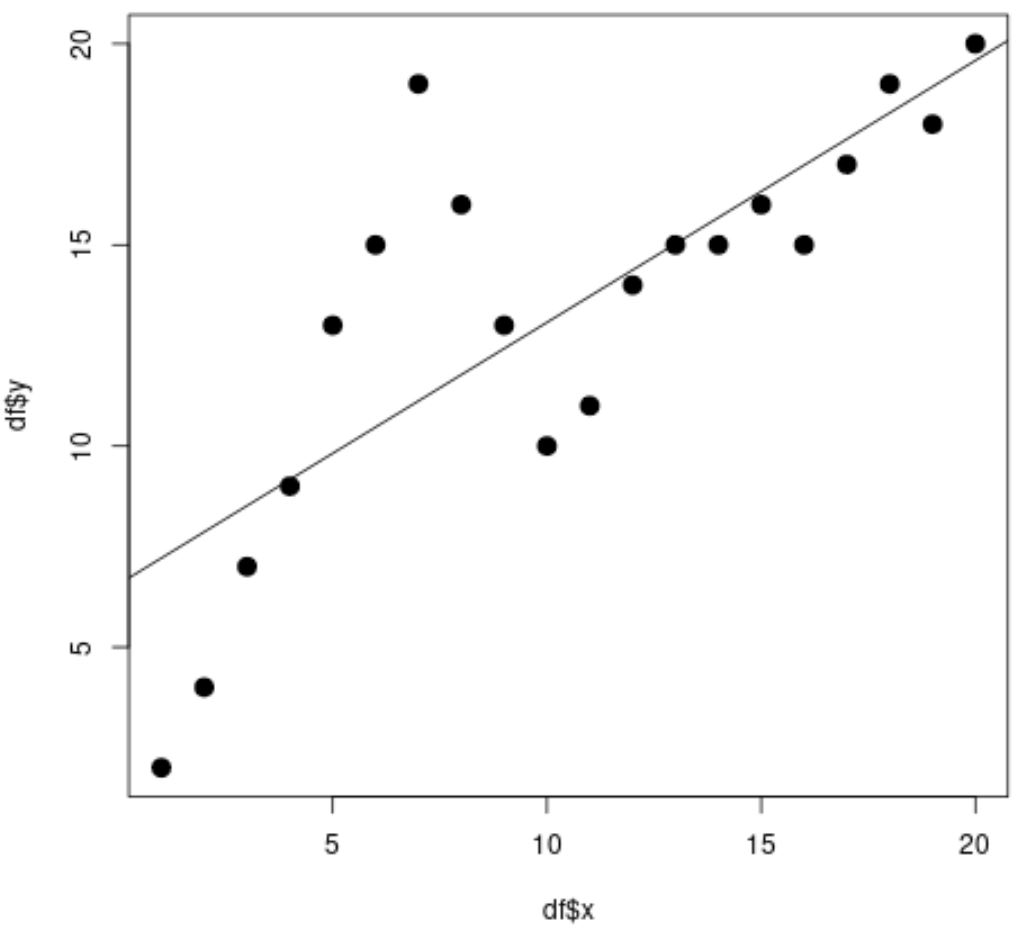
散布図から、単純な線形回帰直線がデータにうまく適合していないことがわかります。

モデルの結果から、調整された R 二乗値が0.5903であることもわかります。

これをスプライン モデルの調整された R 二乗値と比較します。

ステップ 3: スプライン回帰モデルを当てはめる

次に、 splinesパッケージのbs()関数を使用して、2 つのノードを持つスプライン回帰モデルを近似し、近似されたモデルを散布図にプロットしましょう。

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

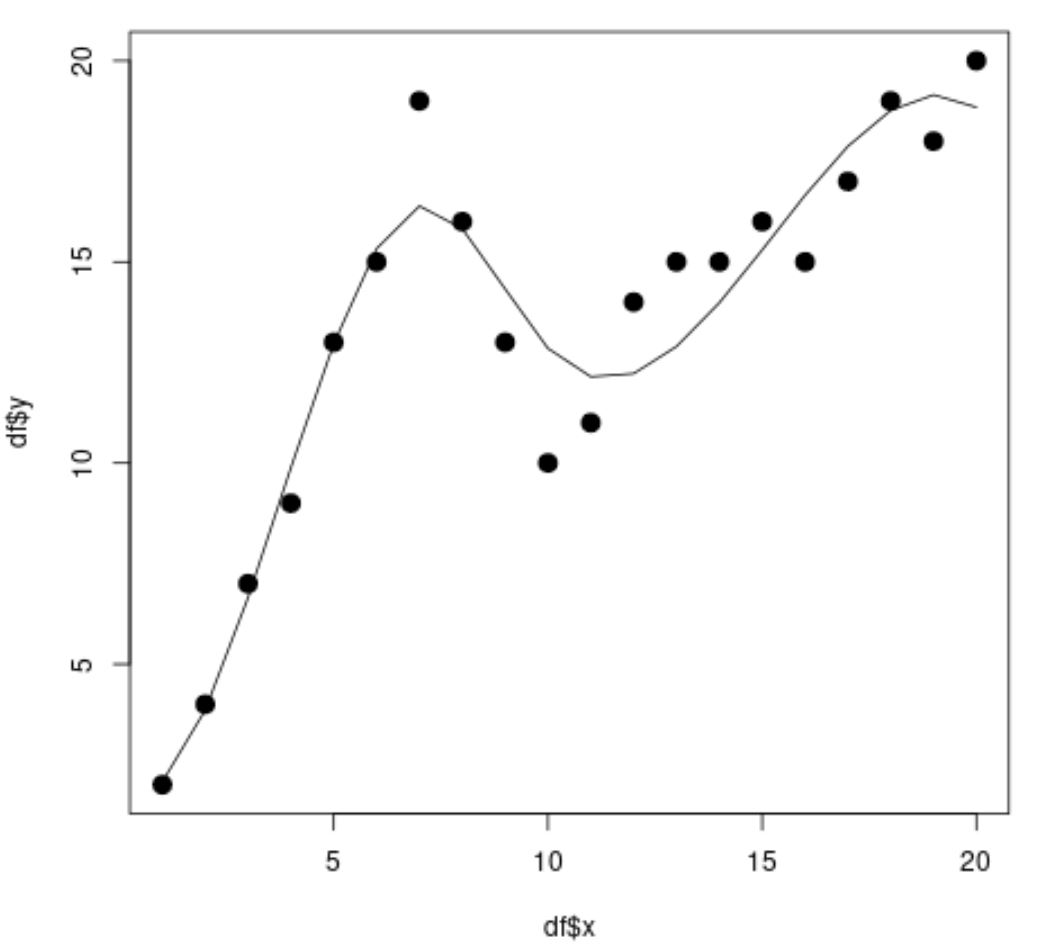
散布図から、スプライン回帰モデルがデータに非常によく適合していることがわかります。

モデルの結果から、調整された R 二乗値が0.8987であることもわかります。

このモデルの調整された R 二乗値は、単純な線形回帰モデルよりもはるかに高く、スプライン回帰モデルがデータによりよく適合できることがわかります。

この例では、ノードが x=7 と x=10 に配置されるように選択したことに注意してください。

実際には、データ内のパターンが変化すると思われる場所と、ドメインの専門知識に基づいて、ノードの場所を自分で選択する必要があります。

追加リソース

次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。

R で重回帰を実行する方法
R で指数回帰を実行する方法
R で加重最小二乗回帰を実行する方法