R での拡張 dickey-fuller テスト (例あり)

時系列に傾向がなく、時間の経過とともに一定の変動を示し、時間の経過とともに一定の自己相関構造がある場合、時系列は「定常」であると言われます。

時系列が定常であるかどうかをテストする 1 つの方法は、次の帰無仮説と対立仮説を使用する拡張ディッキー・フラー検定を実行することです。

H ₀ :時系列は非定常です。言い換えれば、その構造は時間に依存し、その変化は時間の経過とともに一定ではありません。

H _A :時系列は静止しています。

検定のp 値が特定の有意水準 (例: α = 0.05) を下回っている場合、帰無仮説を棄却し、時系列が定常であると結論付けることができます。

次の段階的な例は、特定の時系列に対して R で拡張ディッキー フラー テストを実行する方法を示しています。

例: R での拡張 Dickey-Fuller テスト

R に次の時系列データがあるとします。

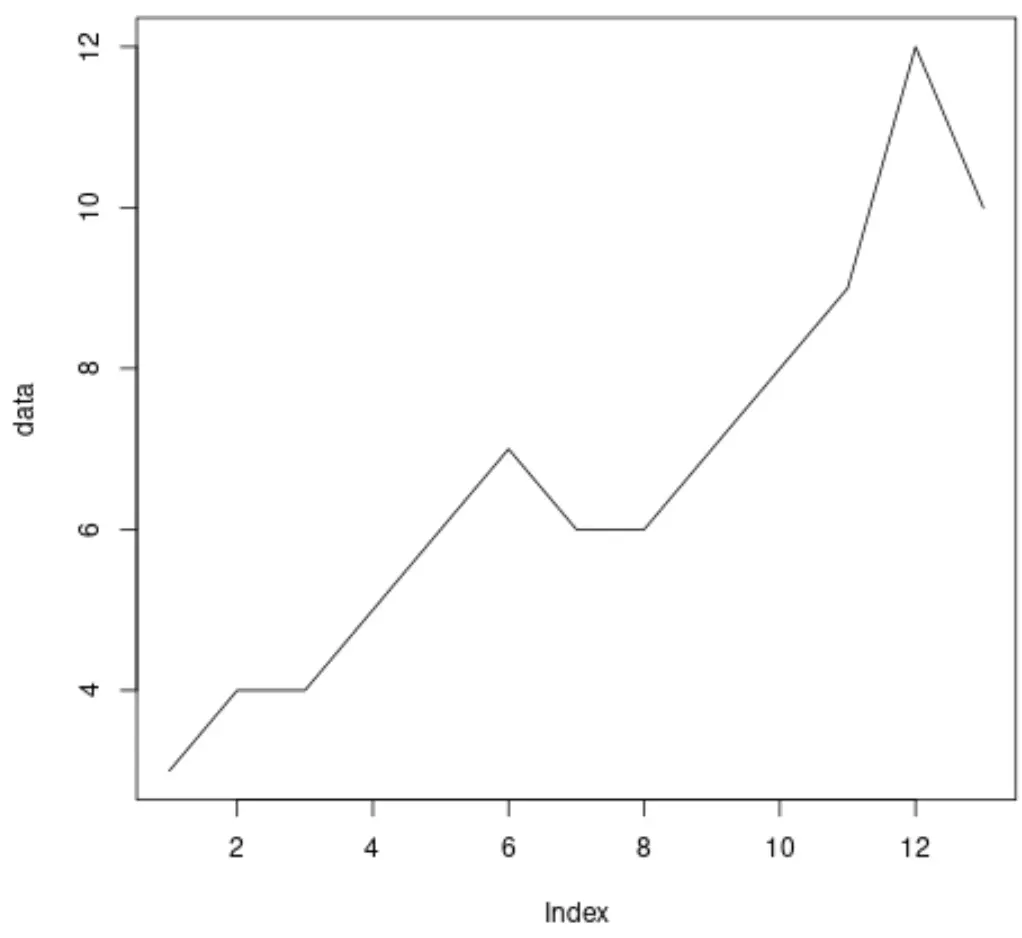
 data <- c(3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10)

データに対して拡張ディッキー・フラー検定を実行する前に、データを視覚化するための簡単なプロットを作成できます。

 plot(data, type=' l ')

拡張された Dickey-Fuller テストを実行するには、 tseriesライブラリのadf.test()関数を使用できます。

次のコードは、この関数の使用方法を示しています。

 library (tseries)

#perform augmented Dickey-Fuller test 
adf.test(data)

	Augmented Dickey-Fuller Test

data:data
Dickey-Fuller = -2.2048, Lag order = 2, p-value = 0.4943
alternative hypothesis: stationary

結果の最も重要な値を解釈する方法は次のとおりです。

• テスト統計: -2.2048
• P 値: 0.4943

p 値は 0.05 未満ではないため、帰無仮説を棄却できません。

これは、時系列が静止していないことを意味します。言い換えれば、その構造は時間に依存し、その変化は時間の経過とともに一定ではありません。

追加リソース

次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。

R で Mann-Kendall トレンド テストを実行する方法
R で時系列をプロットする方法
データの傾向を減らす方法