R でブートストラップする方法 (例付き)
ブートストラップは、 統計の標準誤差を推定し、統計の信頼区間を生成するために使用できる方法です。
ブートストラップの基本的なプロセスは次のとおりです。
- 指定されたデータセットから置換されたk 個の反復サンプルを取得します。
- サンプルごとに、目的の統計を計算します。
- これにより、特定の統計量に対してk 個の異なる推定値が得られ、これを使用して統計量の標準誤差を計算し、統計量の信頼区間を作成できます。
ブートストラップ ライブラリの次の関数を使用して、R でブートストラップできます。
1. ブートストラップ サンプルを生成します。
boot(データ、統計、R、…)
金:
- データ:データのベクトル、行列、またはブロック
- statistic:開始される統計を生成する関数
- A:ブートストラップの繰り返し回数
2. ブートストラップ信頼区間を生成します。
boot.ci(ブートオブジェクト、設定、タイプ)
金:
- bootobject: boot() 関数によって返されるオブジェクト
- conf:計算する信頼区間。デフォルト値は0.95です
- type:計算する信頼区間のタイプ。オプションには「standard」、「basic」、「stud」、「perc」、「bca」、「all」が含まれます。デフォルトは「all」です。
次の例は、これらの関数を実際に使用する方法を示しています。
例 1: 単一の統計をブートストラップする
次のコードは、単純な線形回帰モデルのR 二乗の標準誤差を計算する方法を示しています。
set.seed(0) library (boot) #define function to calculate R-squared rsq_function <- function (formula, data, indices) { d <- data[indices,] #allows boot to select sample fit <- lm(formula, data=d) #fit regression model return (summary(fit)$r.square) #return R-squared of model } #perform bootstrapping with 2000 replications reps <- boot(data=mtcars, statistic=rsq_function, R=2000, formula=mpg~disp) #view results of boostrapping reps ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = mtcars, statistic = rsq_function, R = 2000, formula = mpg ~ available) Bootstrap Statistics: original bias std. error t1* 0.7183433 0.002164339 0.06513426
結果から次のことがわかります。
- この回帰モデルの推定 R 二乗は0.7183433です。
- この推定値の標準誤差は0.06513426です。
ブートストラップされたサンプルの分布をすばやく視覚化することもできます。
plot(reps)
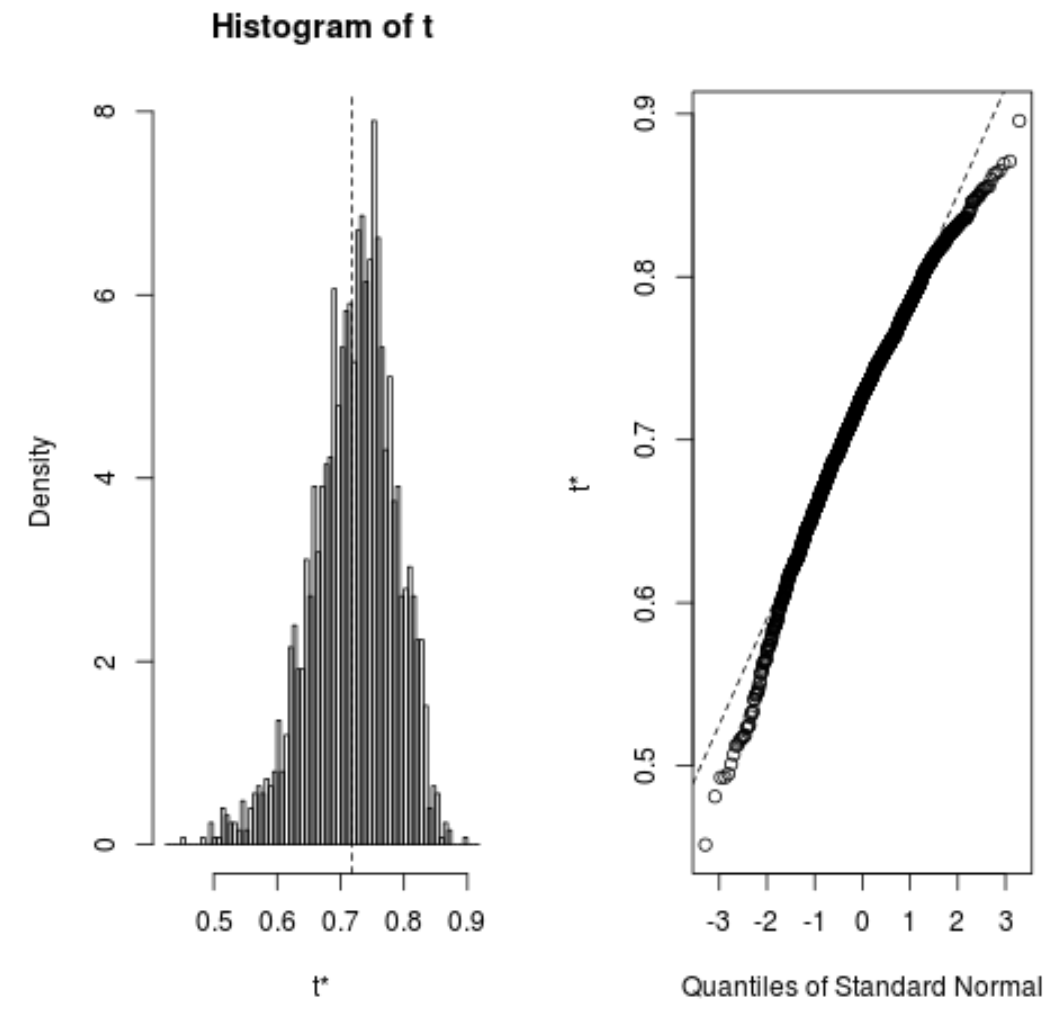
次のコードを使用して、モデルの推定 R 二乗の 95% 信頼区間を計算することもできます。
#calculate adjusted bootstrap percentile (BCa) interval boot.ci(reps, type=" bca ") CALL: boot.ci(boot.out = reps, type = "bca") Intervals: Level BCa 95% (0.5350, 0.8188) Calculations and Intervals on Original Scale
結果から、真の R 二乗値のブートストラップされた 95% 信頼区間は (0.5350, 0.8188) であることがわかります。
例 2: 複数の統計をブートストラップする
次のコードは、重線形回帰モデルの各係数の標準誤差を計算する方法を示しています。
set.seed(0) library (boot) #define function to calculate fitted regression coefficients coef_function <- function (formula, data, indices) { d <- data[indices,] #allows boot to select sample fit <- lm(formula, data=d) #fit regression model return (coef(fit)) #return coefficient estimates of model } #perform bootstrapping with 2000 replications reps <- boot(data=mtcars, statistic=coef_function, R=2000, formula=mpg~disp) #view results of boostrapping reps ORDINARY NONPARAMETRIC BOOTSTRAP Call: boot(data = mtcars, statistic = coef_function, R = 2000, formula = mpg ~ available) Bootstrap Statistics: original bias std. error t1* 29.59985476 -5.058601e-02 1.49354577 t2* -0.04121512 6.549384e-05 0.00527082
結果から次のことがわかります。
- モデル切片の推定係数は29.59985476で、この推定の標準誤差は1.49354577です。
- モデル内の予測変数dispの推定係数は-0.04121512で、この推定の標準誤差は0.00527082です。
ブートストラップされたサンプルの分布をすばやく視覚化することもできます。
plot(reps, index=1) #intercept of model plot(reps, index=2) #disp predictor variable
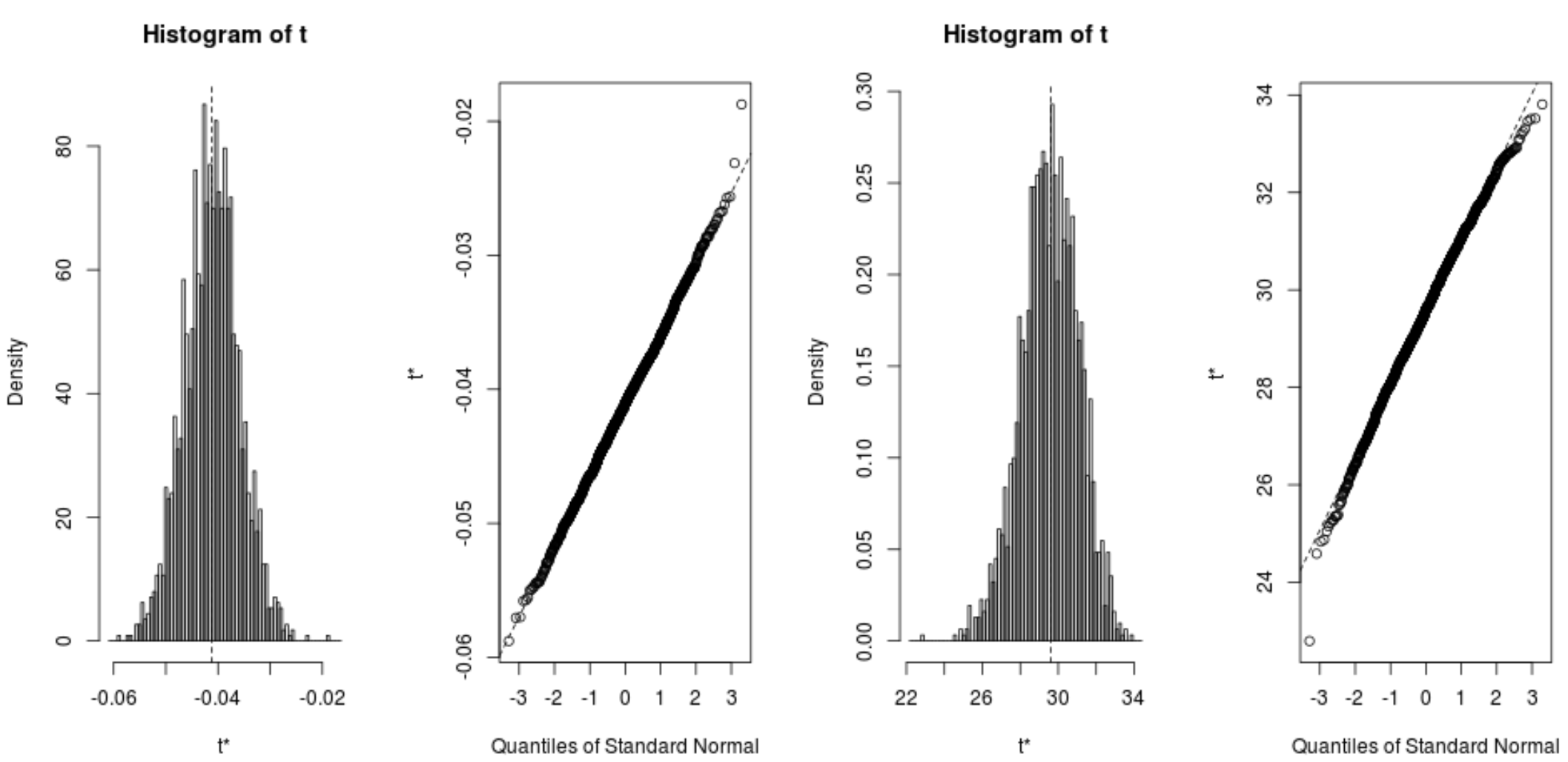
次のコードを使用して、各係数の 95% 信頼区間を計算することもできます。
#calculate adjusted bootstrap percentile (BCa) intervals boot.ci(reps, type=" bca ", index=1) #intercept of model boot.ci(reps, type=" bca ", index=2) #disp predictor variable CALL: boot.ci(boot.out = reps, type = "bca", index = 1) Intervals: Level BCa 95% (26.78, 32.66) Calculations and Intervals on Original Scale BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS Based on 2000 bootstrap replicates CALL: boot.ci(boot.out = reps, type = "bca", index = 2) Intervals: Level BCa 95% (-0.0520, -0.0312) Calculations and Intervals on Original Scale
結果から、モデル係数のブートストラップされた 95% 信頼区間は次のとおりであることがわかります。
- 傍受用IC:(26.78、32.66)
- 表示の CI : (-.0520、-.0312)