R での主成分分析: ステップバイステップの例

主成分分析 (PCA と略されることも多い) は、データセット内の変動の大部分を説明する主成分 (元の予測子の線形結合) を見つけようとする教師なし機械学習手法です。

PCA の目標は、元のデータ セットよりも少ない変数を使用してデータ セット内の変動性のほとんどを説明することです。

p個の変数を含む特定のデータセットについて、変数の各ペアごとの組み合わせの散布図を調べることができますが、散布図の数はすぐに膨大になる可能性があります。

p 個の予測子に対して、p(p-1)/2 個の点群が存在します。

したがって、p = 15 の予測子を持つデータセットの場合、105 個の異なる散布図が存在することになります。

幸いなことに、PCA は、データ内の変動をできるだけ多く捕捉するデータ セットの低次元表現を見つける方法を提供します。

わずか 2 次元でほとんどの変動を捉えることができれば、元のデータセットからのすべての観測値を単純な散布図に投影できます。

主なコンポーネントを見つける方法は次のとおりです。

p個の_{予測子を持つデータセットが与えられたとします}: _

• _{Z m = ΣΦ jm _}
• Z ₁は、可能な限り多くの分散を捕捉する予測子の線形結合です。
• Z _{2 は}、Z ₁と直交している (つまり、無相関である) 一方で、最も多くの分散を捕捉する予測子の次の線形結合です。
• Z ₃は、Z ₂に直交しながら最大の分散を捕捉する予測子の次の線形結合になります。
• 等々。

実際には、次の手順を使用して、元の予測子の線形結合を計算します。

1.平均が 0、標準偏差が 1 になるように各変数をスケールします。

2.スケーリングされた変数の共分散行列を計算します。

3.共分散行列の固有値を計算します。

線形代数を使用すると、最大の固有値に対応する固有ベクトルが第 1 主成分であることがわかります。言い換えれば、この特定の予測子の組み合わせは、データの最大の分散を説明します。

2 番目に大きい固有値に対応する固有ベクトルが 2 番目の主成分となり、以下同様になります。

このチュートリアルでは、R でこのプロセスを実行する方法の段階的な例を示します。

ステップ 1: データをロードする

まず、 Tidyverseパッケージをロードします。このパッケージには、データの視覚化と操作に役立ついくつかの関数が含まれています。

 library (tidyverse)

この例では、R に組み込まれているUSArrestsデータセットを使用します。このデータセットには、1973 年の米国各州の住民 100,000 人あたりの殺人、暴行、および強姦の逮捕数が含まれています。

これには、都市部に住む各州の人口の割合、 UrbanPopも含まれます。

次のコードは、データセットの最初の行をロードして表示する方法を示しています。

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

ステップ 2: 主成分を計算する

データをロードした後、R の組み込み関数prcomp()を使用してデータセットの主成分を計算できます。

主成分を計算する前に、データセット内の各変数が平均 0、標準偏差 1 になるようにスケーリングされるように、必ずscale = TRUEを指定してください。

また、R の固有ベクトルはデフォルトで負の方向を向いているため、-1 を乗算して符号を反転します。

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

第 1 主成分 (PC1) は殺人、暴行、強姦に関して高い値を示しており、この主成分がこれらの変数の最大の変動を表すことを示していることがわかります。

また、第 2 主成分 (PC2) が UrbanPop に対して高い値を示していることもわかります。これは、この主成分が都市人口を強調していることを示しています。

各状態の主成分スコアはresults$xに格納されることに注意してください。また、これらのスコアに -1 を乗算して、符号を反転します。

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

ステップ 3: バイプロットで結果を視覚化する

次に、バイプロットを作成できます。これは、データセット内の各観測値を、最初と 2 番目の主成分を軸として使用する散布図に投影するプロットです。

スケール = 0にすると、プロット内の矢印が荷重を表すようにスケールされることに注意してください。

 biplot(results, scale = 0 )

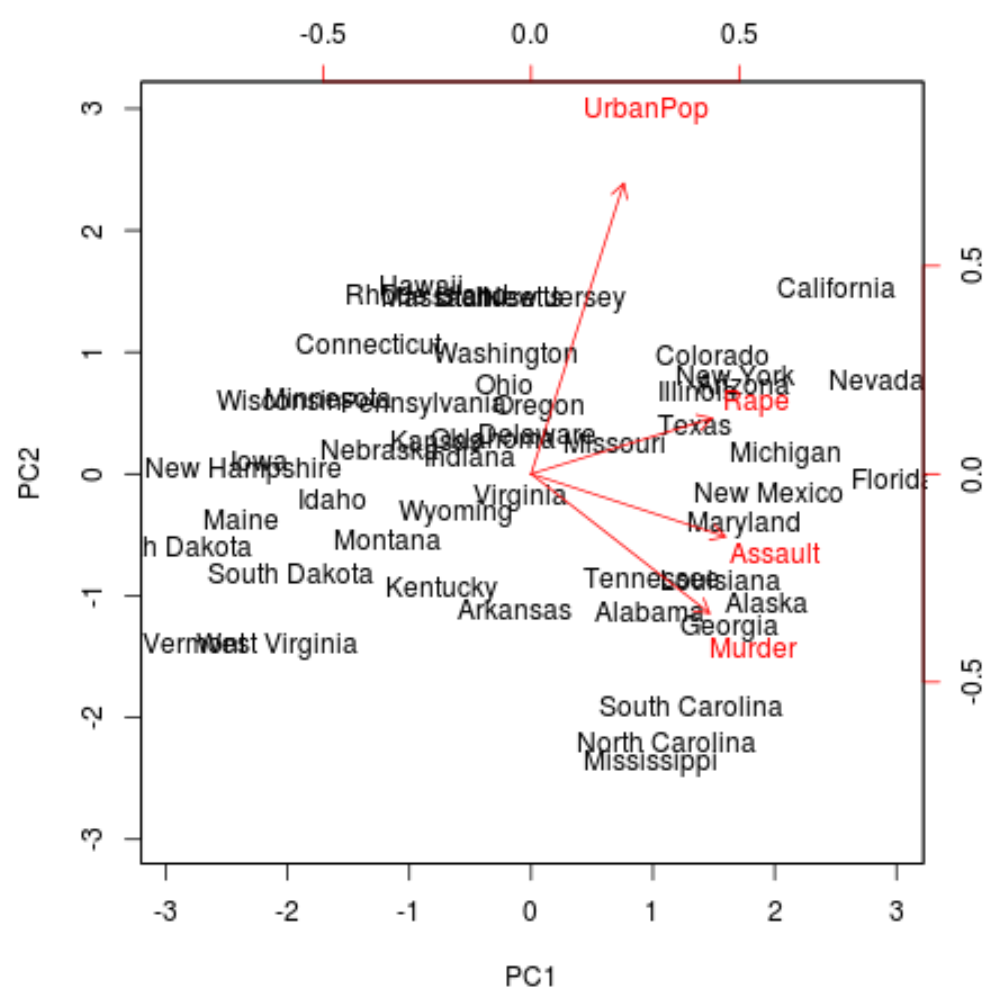
プロットから、50 の各状態が単純な 2 次元空間で表現されていることがわかります。

グラフ上で互いに近い状態は、元のデータセット内の変数に関して類似したデータ パターンを持ちます。

また、一部の州が他の州よりも特定の犯罪とより強く関連していることもわかります。たとえば、ジョージア州は、プロット内の殺人変数に最も近い州です。

元のデータセットで殺人率が最も高い州を見ると、ジョージア州が実際にリストのトップであることがわかります。

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

ステップ 4: 各主成分によって説明される分散を見つける

次のコードを使用して、各主成分によって説明される元のデータセットの合計分散を計算できます。

 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

結果から、次のことがわかります。

• 最初の主成分は、データセット内の合計分散の62%を説明します。
• 2 番目の主成分は、データセット内の合計分散の24.7%を説明します。
• 3 番目の主成分は、データセット内の合計分散の8.9%を説明します。
• 4 番目の主成分は、データセット内の合計分散の4.3%を説明します。

したがって、最初の 2 つの主成分は、データの合計分散の大部分を説明します。

以前のバイプロットでは元のデータの各観測値が最初の 2 つの主成分のみを考慮した散布図に投影されていたため、これは良い兆候です。

したがって、バイプロット内のパターンを調べて、互いに類似した状態を特定することは有効です。

また、スクリー プロット(各主成分によって説明される合計分散を表示するグラフ) を作成して、PCA 結果を視覚化することもできます。

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

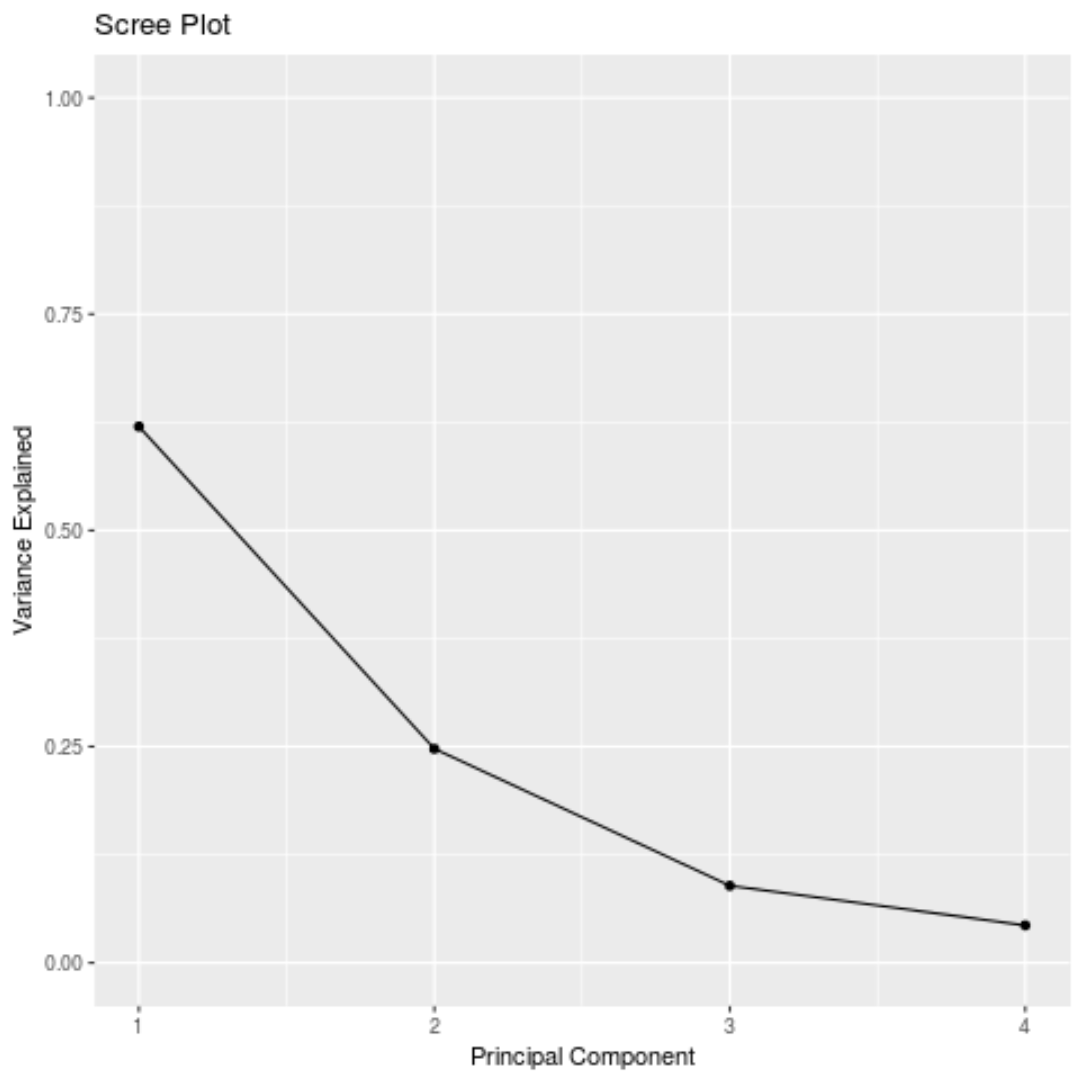
主成分分析の実践

実際には、PCA は次の 2 つの理由で最もよく使用されます。

1. 探索的データ分析– 初めてデータセットを探索し、データ内のどの観測値が互いに最も類似しているかを理解したい場合に、PCA を使用します。

2. 主成分回帰– PCA を使用して主成分を計算し、 主成分回帰で使用することもできます。このタイプの回帰は、データセット内の予測変数間に多重共線性がある場合によく使用されます。

このチュートリアルで使用される完全な R コードは、 ここにあります。