R で相関テストを実行する方法 (例あり)
2 つの変数間の関係を定量化する 1 つの方法は、2 つの変数間の線形関連性の尺度であるピアソン相関係数を使用することです。
常に -1 から 1 までの値を取ります。
- -1 は、2 つの変数間の完全な負の線形相関を示します。
- 0 は 2 つの変数間に線形相関がないことを示します
- 1 は、2 つの変数間の完全な正の線形相関を示します。
相関係数が統計的に有意かどうかを判断するには、対応する t スコアと p 値を計算します。
相関係数 (r) の t スコアを計算する式は次のとおりです。
t = r * √ n-2 / √ 1-r 2
p 値は、自由度 n-2 の t 分布の対応する両側 p 値として計算されます。
例: R での相関テスト
2 つの変数間の相関係数が統計的に有意であるかどうかを判断するには、次の構文を使用して R で相関検定を実行できます。
cor.test(x, y, Method=c(“ピアソン”, “ケンダル”, “スピアマン”))
金:
- x、y:デジタル データ ベクトル。
- メソッド: 2 つのベクトル間の相関を計算するために使用されるメソッド。デフォルトは「ピアソン」です。
たとえば、R に次の 2 つのベクトルがあるとします。
x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23) y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)
2 つの変数間の相関テストを実行する前に、簡単な散布図を作成してそれらの関係を視覚化できます。
#create scatterplot plot(x, y, pch= 16 )
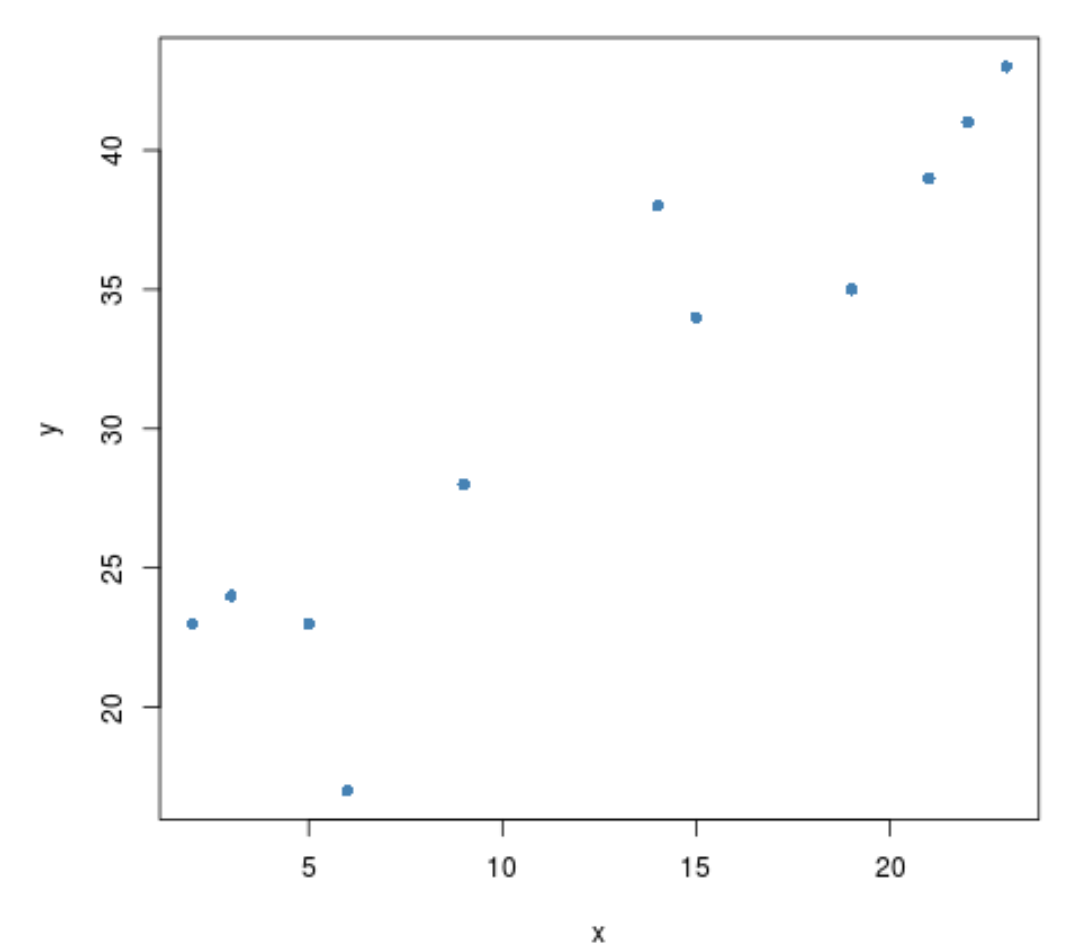
2 つの変数の間には正の相関関係があるようです。つまり、一方が増加すると、他方も同様に増加する傾向があります。
この相関関係が統計的に有意かどうかを確認するには、相関検定を実行します。
#perform correlation test between the two vectors
cor.test(x, y)
Pearson's product-moment correlation
data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7575203 0.9799783
sample estimates:
horn
0.9279869
2 つのベクトル間の相関係数は0.9279869であることがわかります。
検定統計量は7.8756で、対応する p 値は1.35e-05であることがわかります。
この値は 0.05 未満であるため、2 つの変数間の相関関係が統計的に有意であると言える十分な証拠があります。
追加リソース
次のチュートリアルでは、相関係数に関する追加情報を提供します。