R で重回帰結果をプロットする方法

R で単純な線形回帰を実行する場合、単一の予測変数と単一の応答変数のみを扱うため、近似された回帰直線を視覚化するのが簡単です。

たとえば、次のコードは、単純な線形回帰モデルをデータ セットに適合させ、結果をプロットする方法を示しています。

 #create dataset
data <- data.frame(x = c(1, 1, 2, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 11),
                   y = c(13, 14, 17, 23, 24, 25, 25, 24, 28, 32, 33, 35, 40, 41))

#fit simple linear regression model
model <- lm(y ~ x, data = data)

#create scatterplot of data
plot(data$x, data$y)

#add fitted regression line
abline(model)

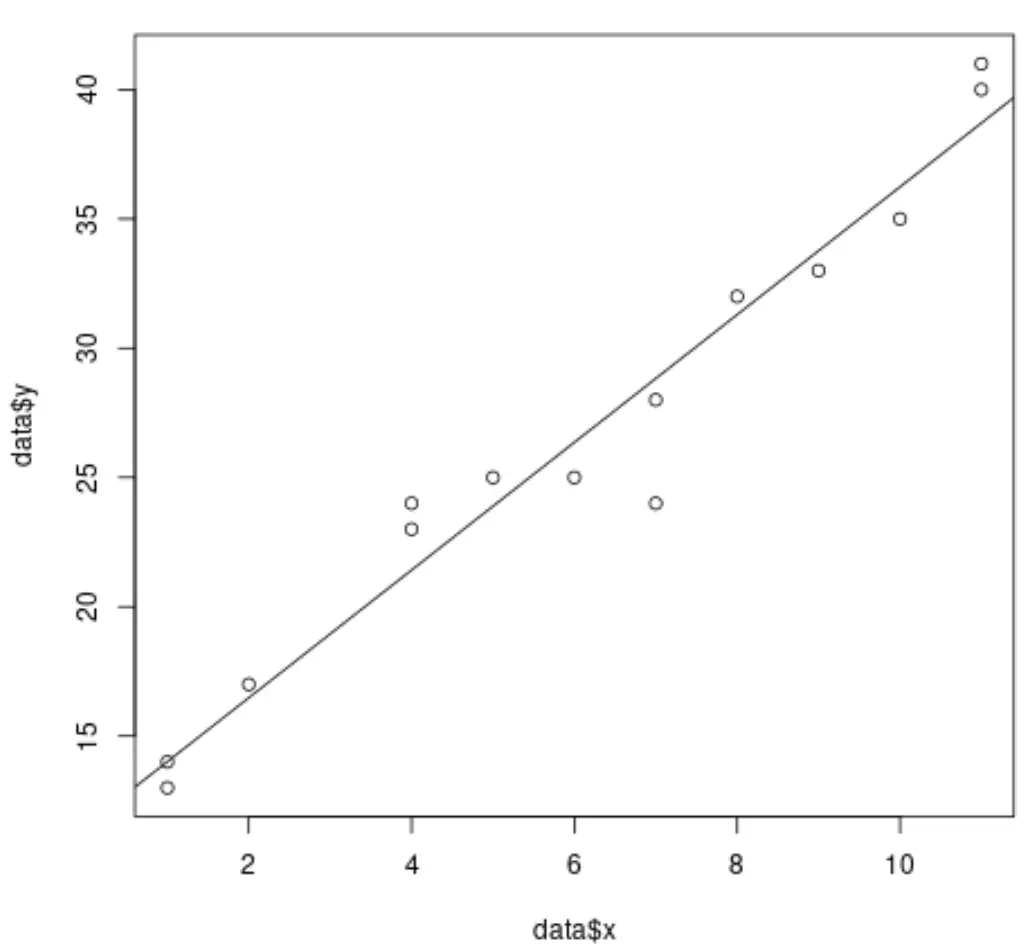
ただし、重線形回帰を実行する場合、複数の予測変数があり、単純に 2D グラフ上に回帰直線をプロットすることができないため、結果を視覚化することが困難になります。

代わりに、追加変数プロット(「偏回帰プロット」と呼ばれることもあります) を使用できます。これは、モデル内の他の予測子変数の存在を制御しながら、応答変数と予測子変数の間の関係を表示する個別のプロットです。

次の例は、R で重回帰を実行し、追加の変数プロットを使用して結果を視覚化する方法を示しています。

例: R での重線形回帰結果のプロット

組み込みのmtcarsデータセットを使用して、次の重線形回帰モデルを R のデータセットに当てはめるとします。

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view results of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

結果から、各係数の p 値が 0.1 未満であることがわかります。わかりやすくするために、各予測変数は有意であり、モデルに含める必要があると仮定します。

追加された変数のプロットを生成するには、 carパッケージのavPlots()関数を使用できます。

 #load car package
library(car)

#produce added variable plots
avPlots(model)

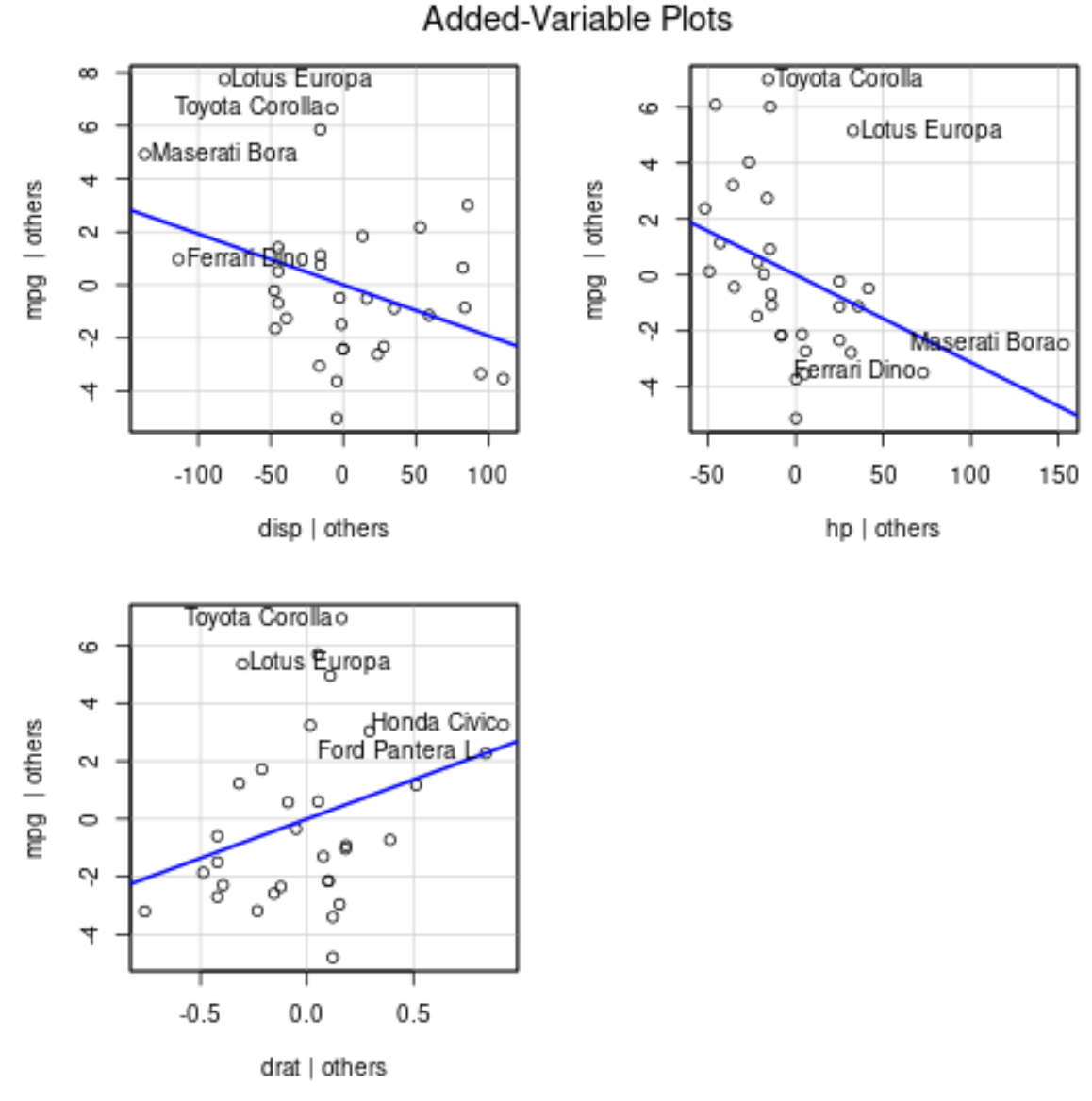
各プロットを解釈する方法は次のとおりです。

• X 軸には単一の予測変数が表示され、Y 軸には応答変数が表示されます。
• 青い線は、他のすべての予測子変数の値を一定に保ちながら、予測子変数と応答変数の間の関連性を示しています。
• 各グラフ内のラベル付き点は、最大の残差を持つ 2 つの観測値と、最大の部分てこ比を持つ 2 つの観測値を表します。

各プロットの線の角度は、推定された回帰式の係数の符号に対応することに注意してください。

たとえば、モデル内の各予測子変数の推定係数は次のとおりです。

• 表示: -0.019232
• ch: -0.031229
• 日付: 2.714975

追加された変数プロットでは、 dratに対して線の角度が正であるのに対し、 dispおよびhpに対しては負であることに注意してください。これは、推定された係数の符号に対応します。

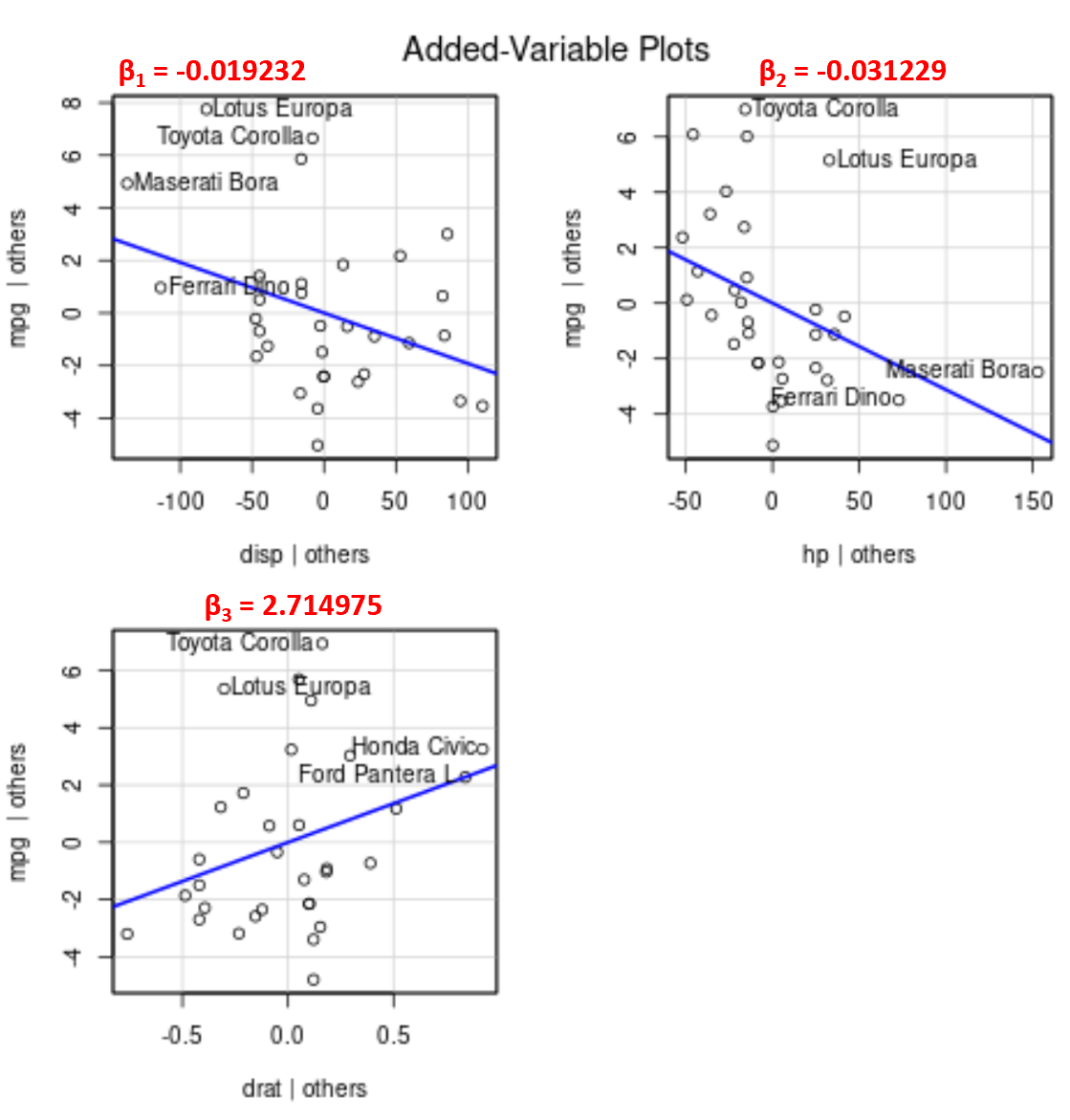
複数の予測変数があるため、2D グラフ上に単一の近似回帰直線をプロットすることはできませんが、これらの追加変数グラフを使用すると、他の予測変数を一定に保ちながら、個々の予測変数と応答変数の間の関係を観察できます。