R のカイ二乗分布: dchisq、pchisq、qchisq、rchisq

このチュートリアルでは、次の関数を使用して R でカイ二乗分布を使用する方法を説明します。

• dchisq : カイ二乗確率密度関数の値を返します。
• pchisq : カイ二乗累積密度関数の値を返します。
• qchisq : カイ二乗分位関数の値を返します。
• rchisq : カイ二乗分布確率変数のベクトルを生成します。

次の例は、これらの各関数を実際に使用する方法を示しています。

ディーキスク

特定の自由度を持つカイ二乗分布をプロットするには、dchisq()関数をCurve()関数とともに使用することがよくあります。

たとえば、次のコードを使用して、5 自由度のカイ二乗分布をプロットできます。

 #plot Chi_Square distribution with 5 degrees of freedom
curve(dchisq(x, df= 5 ), from= 0 , to= 20 )

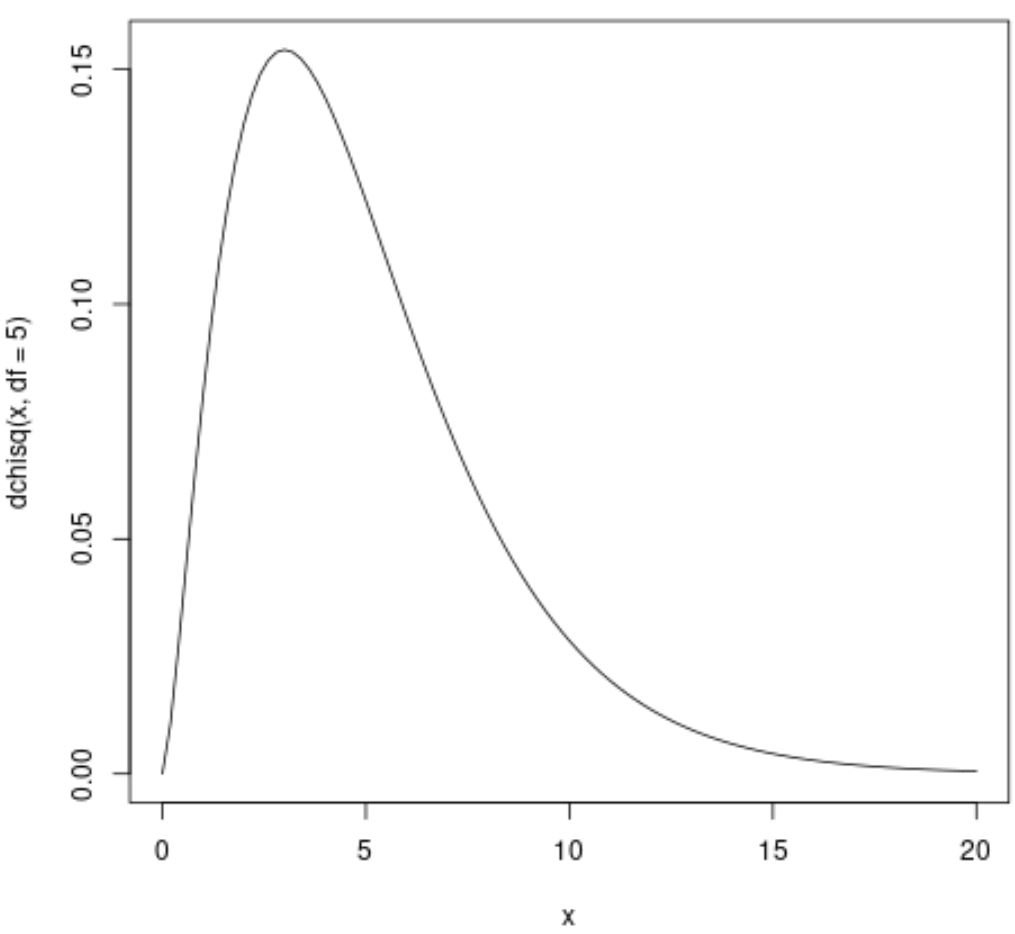
X 軸はカイ二乗検定統計量の値を示し、Y 軸は確率密度関数の対応する値を示します。

関連: R でカイ二乗分布を簡単にプロットする方法

プチスク

私たちはpchisq() をよく使います 関数を使用して、特定のカイ二乗検定統計量に対応するp 値を見つけます。

たとえば、 独立性のカイ二乗検定を実行し、自由度 2 で^X2 = 0.86404 の検定統計量が得られたとします。

pchisq()関数を使用して、この検定統計量に対応する p 値を見つけることができます。

 #calculate p-value for given test statistic with 2 degrees of freedom
1-pchisq(0.86404, df= 2 )

[1] 0.6491964

p 値は0.6491964であることがわかります。

カイ二乗スコアから P 値への計算を使用することによって、これが正しいことを確認することもできます。

何か

qchisq()をよく使います 指定された有意水準と自由度に対応する臨界カイ二乗値を見つける関数。

たとえば、次のコードを使用すると、13 自由度で有意水準 0.05 に対応する臨界カイ 2 乗値を見つけることができます。

 qchisq(p= .95 , df= 13 )

[1] 22.36203

臨界値は22.36203であることがわかります。

カイ二乗臨界値計算ツールを使用して、これが正しいことを確認することもできます。

リスク

rchisq()をよく使用します。  与えられた自由度でカイ二乗分布に従うn 個の乱数値のリストを生成する関数。

たとえば、次のコードを使用して、自由度 5 のカイ二乗分布に従う 1,000 個のランダム値のリストを生成できます。

 #make this example reproducible
set. seed ( 0 ) 

#generate 1000 random values that follow Chi-Square dist with df=5
values <- rchisq(n= 1000 , df= 5 )

#view first five values
head(values)

[1] 8.369701 3.130487 1.985623 5.258747 10.578594 6.360859

この値の分布を視覚化するために、 hist( ) 関数を使用してヒストグラムを生成することもできます。

 #create histogram to visualize distribution of values
hist(values)

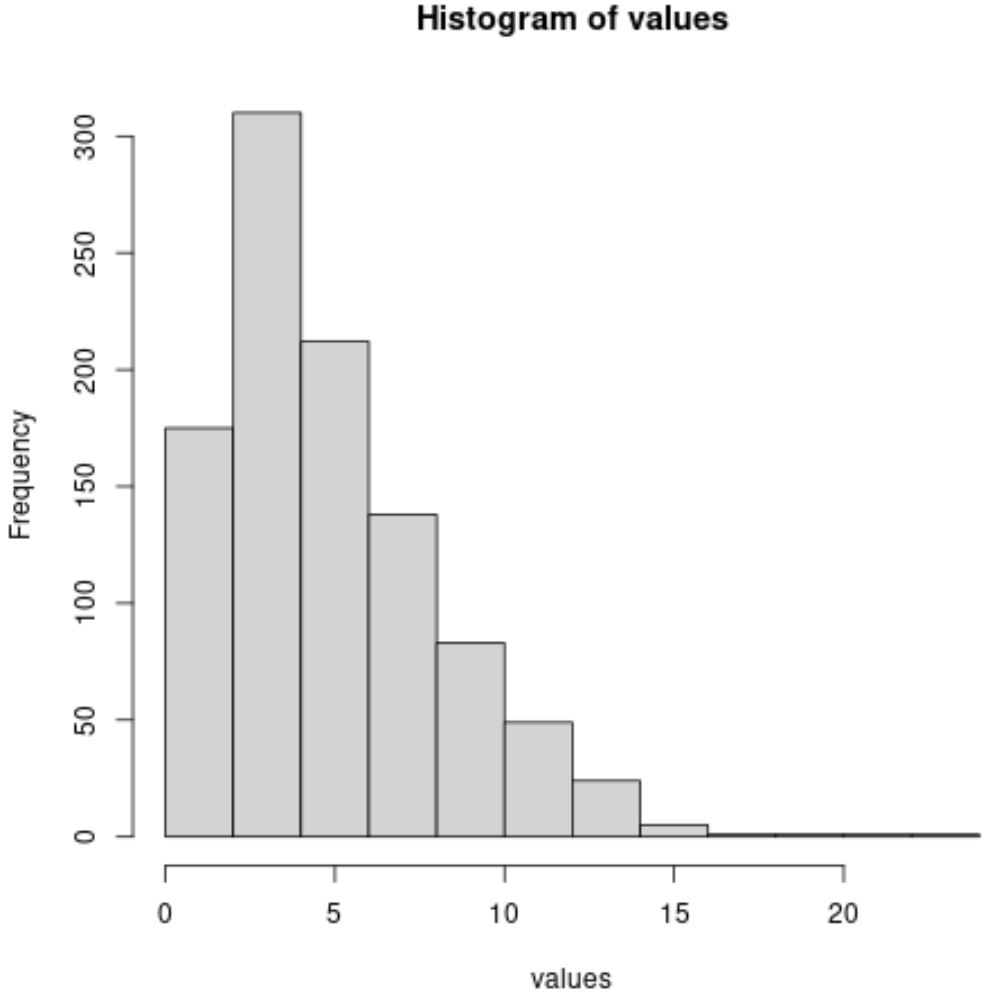
X 軸はデータ値を示し、Y 軸はそれらの値の頻度を示します。

追加リソース

次のチュートリアルでは、R で他のディストリビューションを操作する方法について説明します。

R の正規分布: dnorm、pnorm、qnorm、および rnorm
R の二項分布: dbinom、pbinom、qbinom、rbinom
R での魚の分布: dpois、ppois、qpois、rpois