R で dfbetas を計算する方法

統計では、さまざまな観測値が回帰モデルにどのような影響を与えるかを知りたいことがよくあります。

観測値の影響を計算する 1 つの方法は、 DFBETASとして知られるメトリックを使用することです。これは、個々の観測値を除去することによる各係数に対する標準化された効果を示します。

このメトリクスは、特定の回帰モデルの各係数推定に対する各観測値の影響についてのアイデアを与えてくれます。

このチュートリアルでは、R のモデル内の各観測値の DFBETAS を計算して視覚化する方法を段階的に示します。

ステップ 1: 回帰モデルを作成する

まず、R に組み込まれているmtcarsデータセットを使用して重線形回帰モデルを作成します。

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

ステップ 2: 各観測値の DFBETAS を計算する

次に、組み込みのdfbetas()関数を使用して、モデル内の各観測値の DFBETAS 値を計算します。

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

各観測値について、その特定の観測値を削除したときに発生する原点、 disp変数、およびhp変数の係数推定値の差を確認できます。

一般に、観測値の DBETAS 値がしきい値 2/√ n ( nは観測値の数) より大きい場合、観測値は特定の係数の推定に強い影響を与えていると考えられます。

この例では、しきい値は0.3535534になります。

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

ステップ 3: DFBETAS を視覚化する

最後に、モデル内の各観測値と各予測子の DFBETAS 値を視覚化するプロットを作成できます。

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

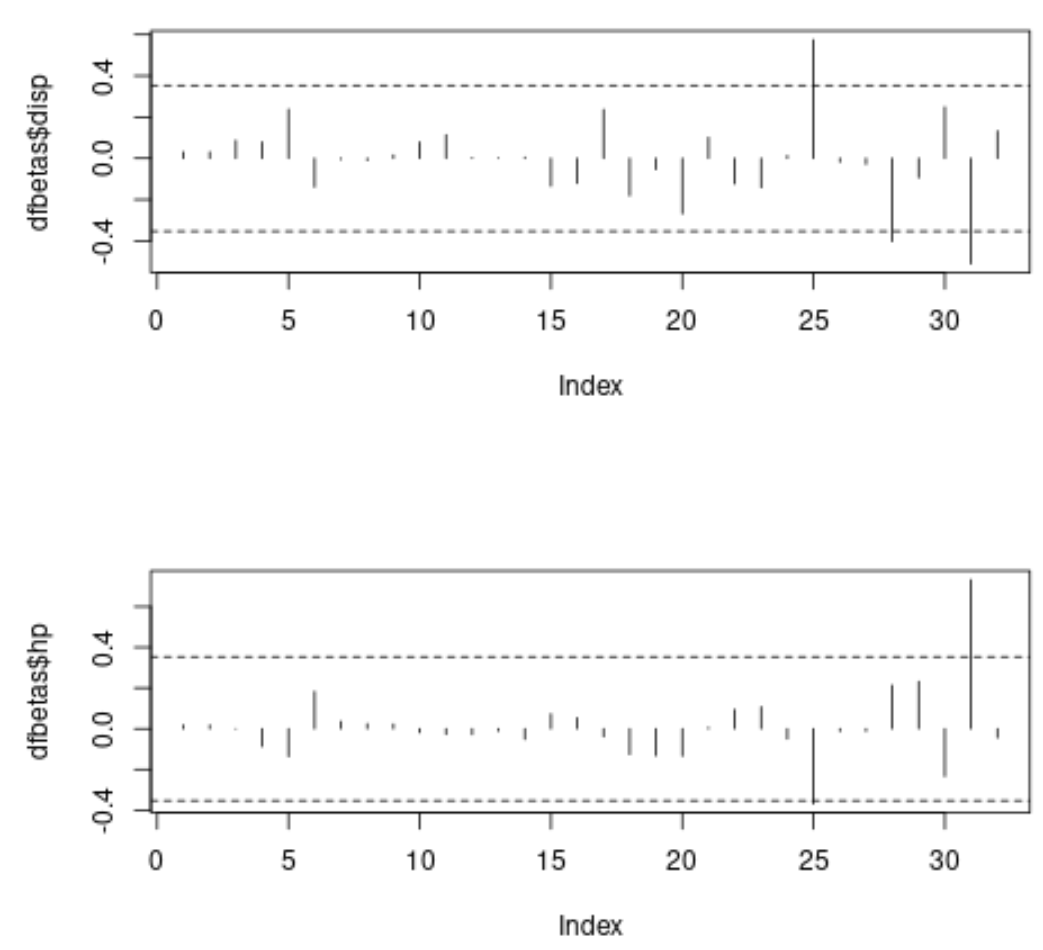
各プロットでは、X 軸はデータセット内の各観測値のインデックスを表示し、Y 値は各観測値と各予測子の対応する DFBETAS を表示します。

最初のプロットでは、3 つの観測値が絶対しきい値0.3535534を超えていることがわかり、2 番目のプロットでは、2 つの観測値が絶対しきい値を超えていることがわかります。

これらの観測値がモデル係数の推定に不当な影響を与えているかどうかを判断するために、これらの観測値をより詳しく調査することを選択する場合があります。

追加リソース

R で単純な線形回帰を実行する方法
R で重回帰を実行する方法
R でレバレッジ統計を計算する方法
R で DFFITS を計算する方法