R でのブラウン フォーサイス テスト: ステップバイステップの例

一元配置分散分析は、 3 つ以上の独立したグループの平均値間に有意差があるかどうかを判断するために使用されます。

一元配置分散分析の仮定の 1 つは、 サンプルの抽出元となる母集団の分散が等しいということです。

これをテストする最も一般的な方法の 1 つは、ブラウン フォーサイス テストを使用することです。これは、次の仮定を使用する統計テストです。

• H ₀ :母集団間の分散は等しい。
• H _A : 集団間の差異は等しくありません。

検定のp 値が特定の有意水準 (例: α = 0.05) を下回っている場合、帰無仮説は棄却され、異なる母集団間で分散は等しくないと結論付けられます。

このチュートリアルでは、R でブラウン フォーサイス テストを実行する方法の例を段階的に説明します。

ステップ 1: データを入力する

3 つの異なるトレーニング プログラムが異なるレベルの減量につながるかどうかを知りたいとします。

これをテストするために、90 人を募集し、各プログラムの使用にランダムに 30 人を割り当てます。次に、1か月後の各人の体重減少を測定します。

次のデータセットには、各プログラムで減少した体重に関する情報が含まれています。

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

ステップ 2: データを要約して視覚化する

ブラウン フォーサイス検定を実行する前に、箱ひげ図を作成して、各グループの体重減少の分散を視覚化できます。

 boxplot(weight_loss ~ program, data = data)

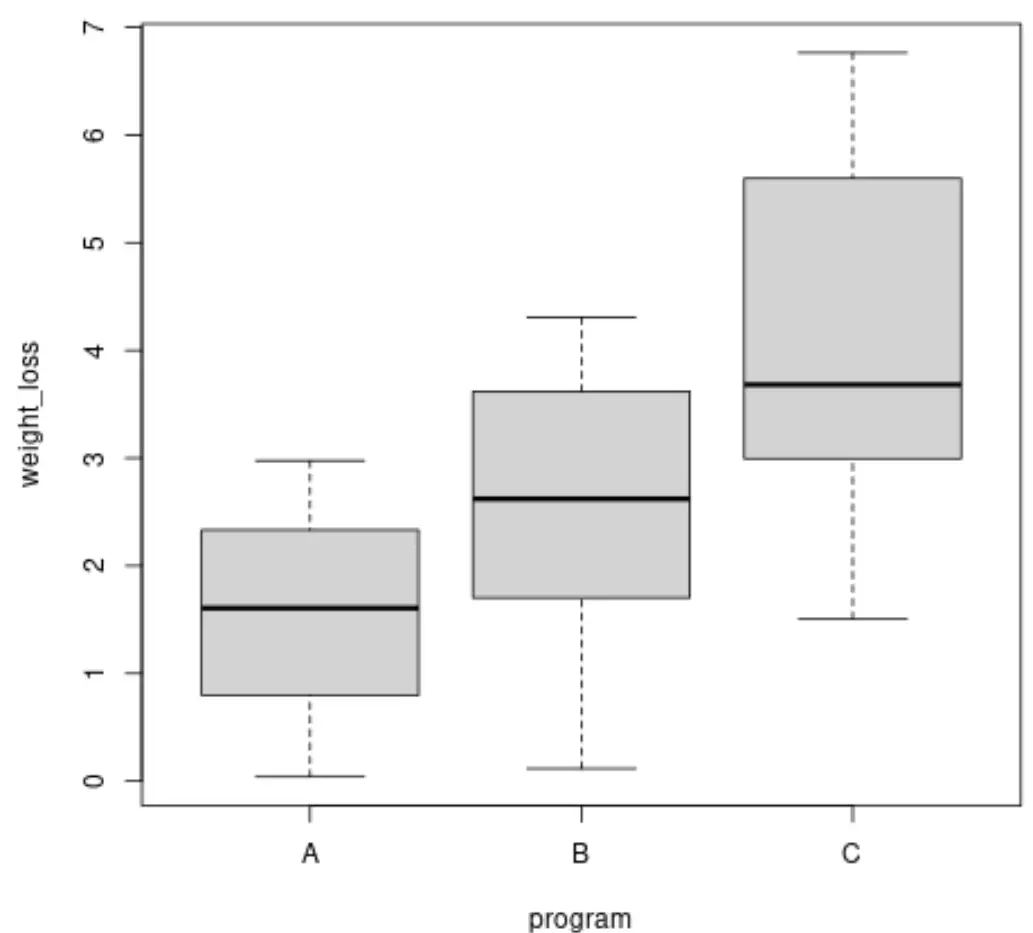
各グループの体重減少の分散を計算することもできます。

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

グループ間の分散が異なることがわかりますが、これらの差異が 統計的に有意であるかどうかを判断するには、ブラウン-フォーサイス検定を実行できます。

ステップ 3: ブラウン・フォーサイス検定を実行する

R でブラウン フォーサイス テストを実行するには、 onewaytestsパッケージのbf.test()関数を使用できます。

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

検定の p 値は 0.000 未満であることがわかり、結果が示すように、3 つのグループ間の分散の差は統計的に有意です。

次のステップ

ブラウン-フォーサイス検定の帰無仮説を棄却できない場合は、データに対して一元配置分散分析を実行できます。

ただし、帰無仮説を棄却すると、分散が等しいという仮定に違反することになります。この場合、次の 2 つのオプションがあります。

1. とにかく一元配置分散分析を実行します。

一元配置分散分析は、最大分散が最小分散の 4 倍を超えない限り、実際には不等分散に対して堅牢であることがわかります。

上記の例のステップ 2 では、最小分散は 0.819、最大分散は 2.46 であることがわかりました。したがって、最大分散と最小分散の比率は 2.46 / 0.819 = 3.003となります。

この値は 4 未満であるため、単純に一元配置分散分析を行うことができます。

2. クラスカル・ウォリス検定を実行する

最大分散と最小分散の比が 4 より大きい場合は、代わりにクラスカル ウォリス検定を実行することを選択できます。これは、一元配置 ANOVA と同等のノンパラメトリックとみなされます。

ここで、 R でのクラスカル-ウォリス検定の段階的な例を見つけることができます。