R でロバスト回帰を実行する方法 (ステップバイステップ)

ロバスト回帰は、作業しているデータセットに外れ値や影響力のある観測値がある場合に、通常の最小二乗回帰の代替として使用できる方法です。

R で堅牢な回帰を実行するには、 MASSパッケージのrlm()関数を使用できます。この関数は次の構文を使用します。

次のステップバイステップの例は、特定のデータセットに対して R でロバスト回帰を実行する方法を示しています。

ステップ 1: データを作成する

まず、操作する偽のデータセットを作成しましょう。

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

ステップ 2: 通常の最小二乗回帰を実行する

次に、通常の最小二乗回帰モデルを当てはめて、標準化された残差のプロットを作成しましょう。

実際には、絶対値が 3 より大きい標準化残差を外れ値と見なすことがよくあります。

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

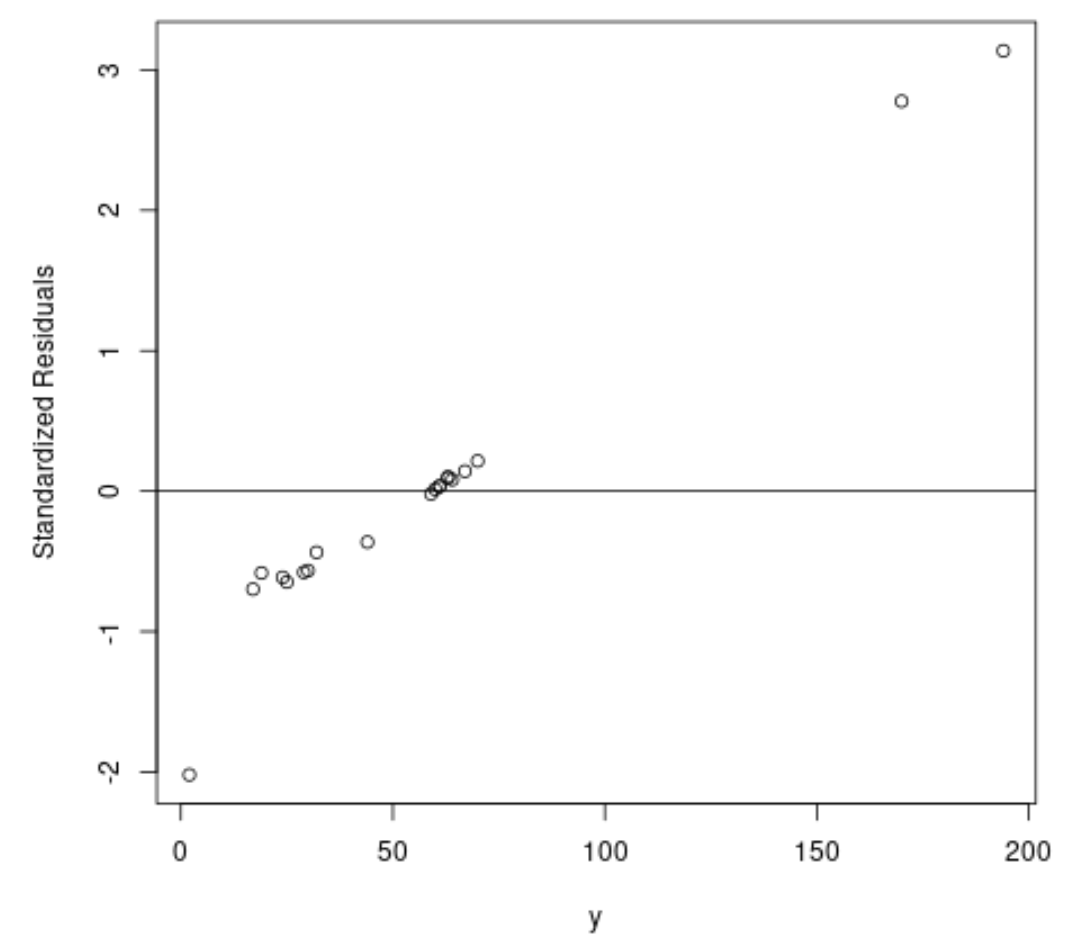
グラフから、標準化残差が約 3 である観測値が 2 つあることがわかります。

これは、データセット内に 2 つの潜在的な外れ値が存在するため、代わりにロバスト回帰の恩恵を受ける可能性があることを示しています。

ステップ 3: ロバスト回帰を実行する

次に、 rlm()関数を使用して、堅牢な回帰モデルを当てはめてみましょう。

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

このロバストな回帰モデルが OLS モデルと比較してデータによりよく適合するかどうかを判断するには、各モデルの残差標準誤差を計算します。

残差標準誤差 (RSE) は、回帰モデルの残差の標準偏差を測定する方法です。 CSR 値が低いほど、モデルはデータに適合しやすくなります。

次のコードは、各モデルの RSE を計算する方法を示しています。

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

ロバスト回帰モデルの RSE は、通常の最小二乗回帰モデルの RSE よりもはるかに低いことがわかります。これは、ロバスト回帰モデルがデータによりよく適合していることを示しています。

追加リソース

R で単純な線形回帰を実行する方法
R で重回帰を実行する方法
R で多項式回帰を実行する方法