R で二変量正規分布をシミュレートしてプロットする方法

統計学では、2 つの変数を加算したときに正規分布が得られる場合、2 つの変数は二変量正規分布に従います。

このチュートリアルでは、R で次のタスクを実行する方法について説明します。

• 二変量正規分布をシミュレートする
• 等高線プロット (2D プロット) を使用して二変量正規分布をプロットします。
• 曲面プロット (3D プロット) を使用して二変量正規分布をプロットする

さあ行こう！

例 1: R で二変量正規分布をシミュレートする

R で二変量正規分布をシミュレートする最も簡単な方法は、 MASSパッケージのmvrnorm()関数を使用することです。

次のコードは、この関数を使用して実際に二変量正規分布をシミュレートする方法を示しています。

 library (MASS)

#make this example reproducible
set. seed ( 0 )

#simulate bivariate normal distribution
bivariate_data <- as. data . frame (mvrnorm(n= 100 ,
                                        mu=c(0, 0),
                                        Sigma=matrix(c(5, 3, 4, 4), ncol= 2 )))

#view first six rows of bivariate dataset
head(bivariate_data)

           V1 V2
1 -2.03600343 -2.9623059
2 0.07719131 1.2948982
3 -3.26729701 -1.7928069
4 -2.62985132 -2.3015471
5 -1.75126215 0.3056698
6 3.67698436 2.2020238

mvrnorm()関数の各引数の動作は次のとおりです。

• n : サンプルサイズを定義します
• mu : 各変数の平均を定義します
• Sigma : 2 つの変数の共分散行列を定義します。

最終結果は、合計すると正規分布に従う 2 つの変数を含むデータ フレームになります。

例 2:二変量正規分布のプロット

R で二変量正規分布をプロットする最も簡単な方法は、 mnormt()パッケージの関数を使用することです。

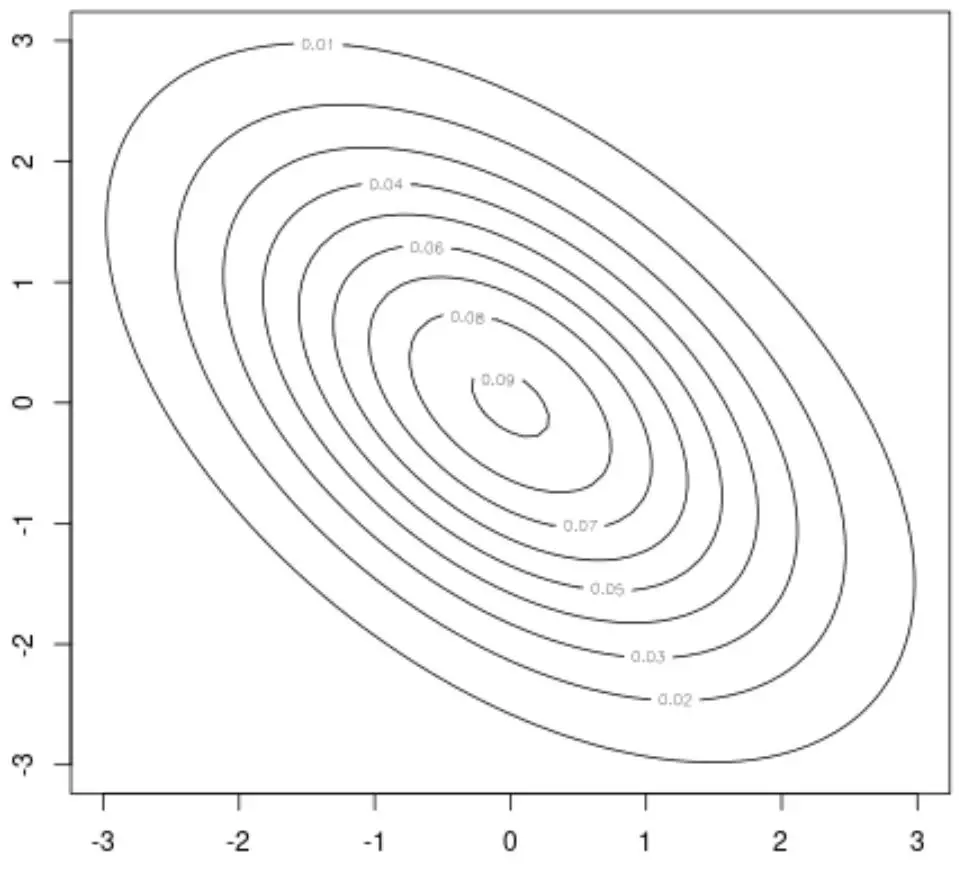
たとえば、このパッケージのcontour()関数を使用して、二変量正規分布の 2D 視覚化を提供する等高線プロットを作成できます。

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create contour plot
contour(x, y, z)

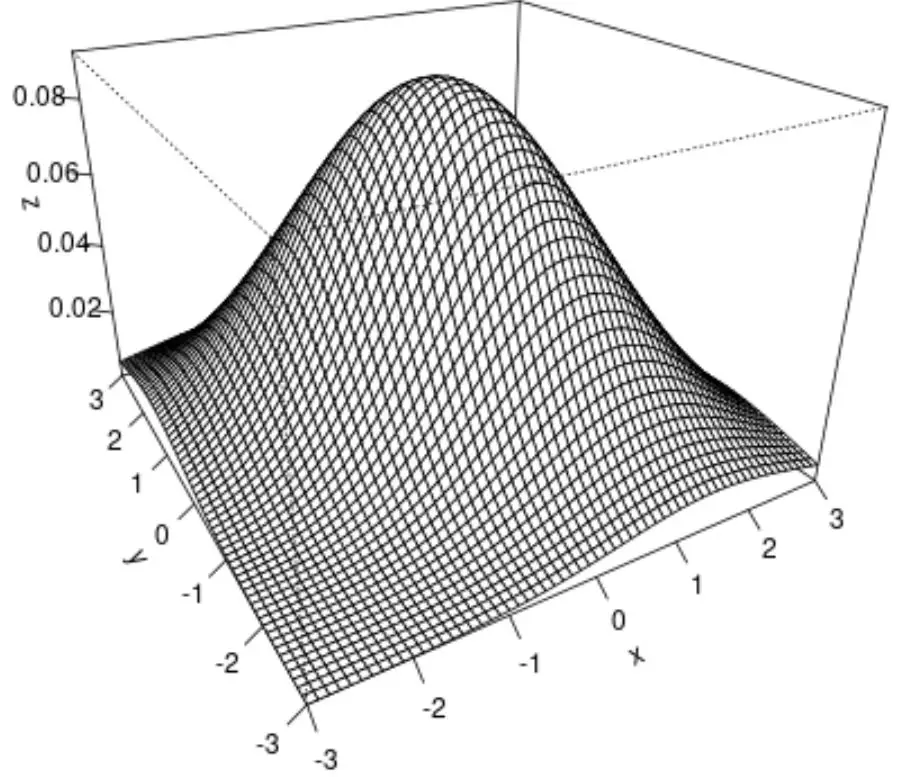
persp()関数を使用して曲面プロットを作成することもできます。これにより、二変量正規分布を 3D 視覚化できます。

 library (mnormt)

#make this example reproducible
set. seed ( 0 )

#create bivariate normal distribution
x <- seq(-3, 3, 0.1) 
y <- seq(-3, 3, 0.1)
mu <- c(0, 0)
sigma <- matrix(c(2, -1, -1, 2), nrow= 2 )
f <- function(x, y) dmnorm(cbind(x, y), mu, sigma)
z <- outer(x, y, f)

#create surface plot
persp(x, y, z, theta= -30 , phi= 25 , expand= 0.6 , ticktype=' detailed ')

persp()関数の各引数の動作は次のとおりです。

• theta、phi : 視線方向の角度を設定します。
• Expand : Z 軸のサイズを制御します。
• tinytype : 軸上の目盛りの外観を制御します。

最終結果は、二変量正規分布の 3D 表面プロットです。

追加リソース

次のチュートリアルでは、R で他の確率分布を使用する方法を説明します。

Rで正規分布を使用する方法
R で二項分布を使用する方法
R でポアソン分布を使用する方法
R で多項分布を使用する方法