R で分類木と回帰木を当てはめる方法

一連の予測変数と応答変数の間の関係が線形の場合、重線形回帰などの方法で正確な予測モデルを生成できます。

ただし、一連の予測変数と応答の間の関係がより複雑な場合、多くの場合、非線形手法の方がより正確なモデルを生成できます。

そのような方法の 1 つが分類回帰ツリー(CART) です。これは、一連の予測子変数を使用して、応答変数の値を予測する決定木を作成します。

応答変数が連続型の場合は回帰ツリーを構築でき、応答変数がカテゴリ型の場合は分類ツリーを構築できます。

このチュートリアルでは、R で回帰ツリーと分類ツリーを作成する方法について説明します。

例 1: R での回帰ツリーの構築

この例では、 ISLRパッケージのHittersデータセットを使用します。これには、263 人のプロ野球選手に関するさまざまな情報が含まれています。

このデータセットを使用して、ホームランと出場年数の予測変数を使用して特定の選手の年俸を予測する回帰ツリーを構築します。

この回帰ツリーを作成するには、次の手順を使用します。

ステップ 1: 必要なパッケージをロードします。

まず、この例に必要なパッケージをロードします。

 library (ISLR) #contains Hitters dataset
library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

ステップ 2: 初期回帰ツリーを構築します。

まず、大規模な初期回帰ツリーを構築します。 「複雑さパラメーター」を表すcpに小さな値を使用することで、ツリーが大きいことを保証できます。

これは、モデル全体の R 二乗が少なくとも cp で指定された値だけ増加する限り、回帰ツリーでさらに分割を実行することを意味します。

次に、 printcp()関数を使用してモデルの結果を出力します。

 #build the initial tree
tree <- rpart(Salary ~ Years + HmRun, data=Hitters, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] HmRun Years

Root node error: 53319113/263 = 202734

n=263 (59 observations deleted due to missingness)

           CP nsplit rel error xerror xstd
1 0.24674996 0 1.00000 1.00756 0.13890
2 0.10806932 1 0.75325 0.76438 0.12828
3 0.01865610 2 0.64518 0.70295 0.12769
4 0.01761100 3 0.62652 0.70339 0.12337
5 0.01747617 4 0.60891 0.70339 0.12337
6 0.01038188 5 0.59144 0.66629 0.11817
7 0.01038065 6 0.58106 0.65697 0.11687
8 0.00731045 8 0.56029 0.67177 0.11913
9 0.00714883 9 0.55298 0.67881 0.11960
10 0.00708618 10 0.54583 0.68034 0.11988
11 0.00516285 12 0.53166 0.68427 0.11997
12 0.00445345 13 0.52650 0.68994 0.11996
13 0.00406069 14 0.52205 0.68988 0.11940
14 0.00264728 15 0.51799 0.68874 0.11916
15 0.00196586 16 0.51534 0.68638 0.12043
16 0.00016686 17 0.51337 0.67577 0.11635
17 0.00010000 18 0.51321 0.67576 0.11615
n=263 (59 observations deleted due to missingness)

ステップ 3: 木を剪定します。

次に、回帰ツリーを枝刈りして、テスト誤差を最小にする cp (複雑さのパラメーター) に使用する最適な値を見つけます。

cp の最適値は、前の出力で最小のx 誤差をもたらす値であることに注意してください。これは、相互検証データからの観測値の誤差を表します。

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

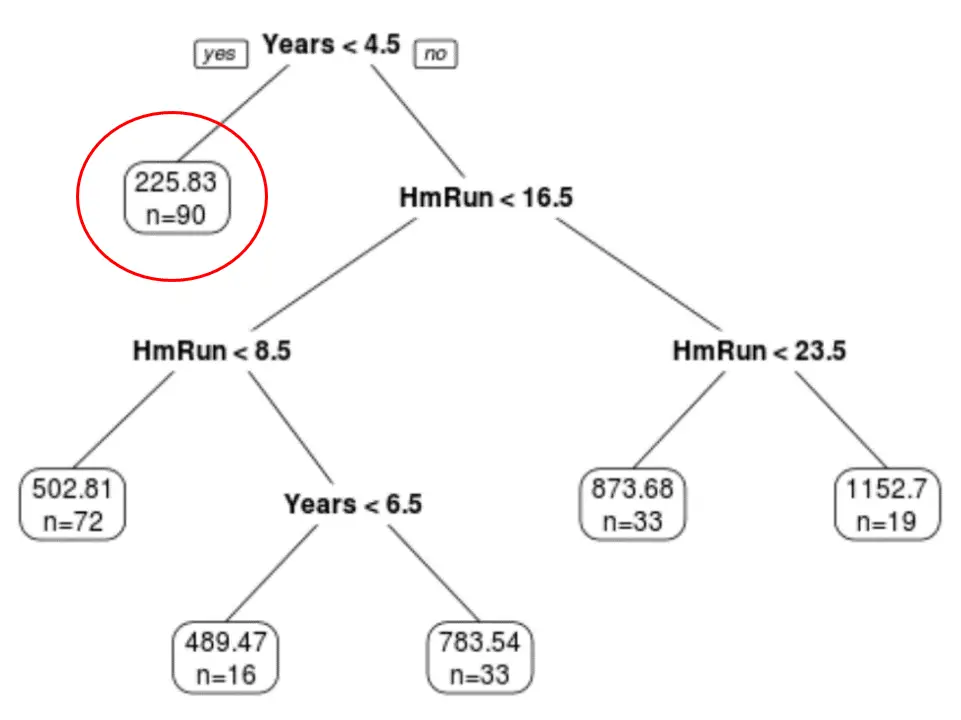
最終的に枝刈りされたツリーには 6 つの終端ノードがあることがわかります。各リーフ ノードには、そのノード内の選手の予測年俸と、そのグレードに属する元のデータセットからの観測値の数が表示されます。

たとえば、元のデータセットには、経験が 4.5 年未満のプレーヤーが 90 人いて、平均給与が 225.83,000 ドルであったことがわかります。

ステップ 4: ツリーを使用して予測を行います。

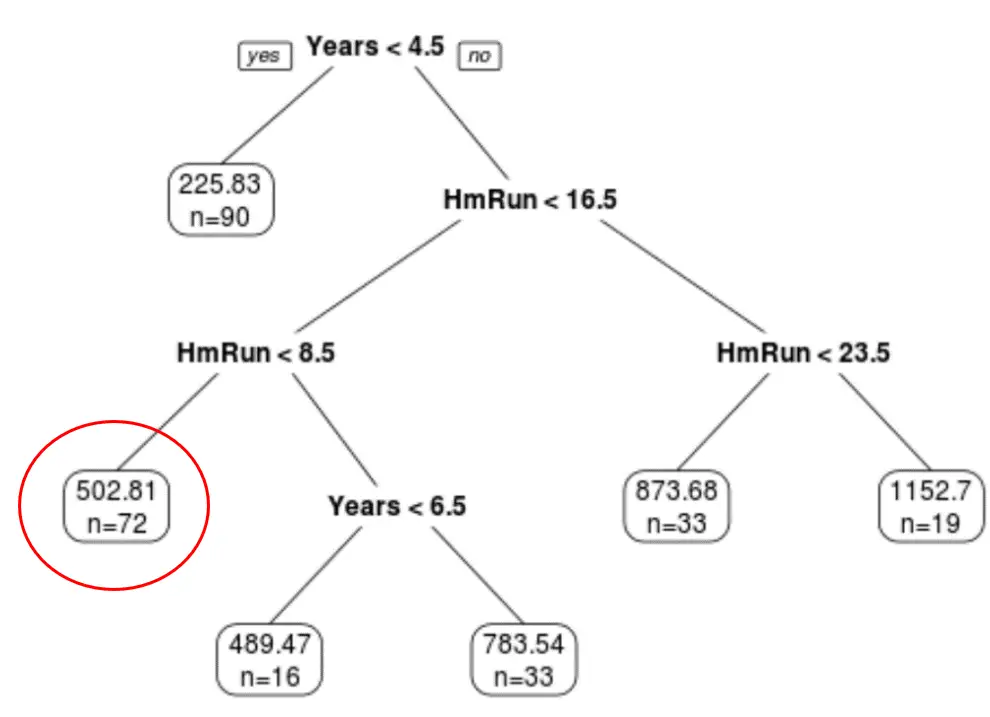
最終的に剪定された木を使用して、特定の選手の年俸と平均ホームランに基づいてその選手の年俸を予測できます。

たとえば、7 年の経験と平均 4 本塁打のプレーヤーの期待年俸は502.81,000 ドルです。

R のdetect()関数を使用してこれを確認できます。

 #define new player
new <- data.frame(Years=7, HmRun=4)

#use pruned tree to predict salary of this player
predict(pruned_tree, newdata=new)

502.8079

例 2: R で分類ツリーを構築する

この例では、 rpart.plotパッケージのptitanicデータセットを使用します。これには、タイタニック号の乗客に関するさまざまな情報が含まれています。

このデータセットを使用して、予測子変数class 、性別、および年齢を使用して特定の乗客が生存したかどうかを予測する分類ツリーを作成します。

この分類ツリーを作成するには、次の手順を使用します。

ステップ 1: 必要なパッケージをロードします。

まず、この例に必要なパッケージをロードします。

 library (rpart) #for fitting decision trees
library (rpart.plot) #for plotting decision trees

ステップ 2: 初期分類ツリーを構築します。

まず、大規模な初期分類ツリーを構築します。 「複雑さパラメーター」を表すcpに小さな値を使用することで、ツリーが大きいことを保証できます。

これは、モデル全体の適合度が少なくとも cp で指定された値だけ増加する限り、分類ツリーでさらに分割を実行することを意味します。

次に、 printcp()関数を使用してモデルの結果を出力します。

 #build the initial tree
tree <- rpart(survived~pclass+sex+age, data=ptitanic, control=rpart. control (cp= .0001 ))

#view results
printcp(tree)

Variables actually used in tree construction:
[1] age pclass sex   

Root node error: 500/1309 = 0.38197

n=1309 

      CP nsplit rel error xerror xstd
1 0.4240 0 1.000 1.000 0.035158
2 0.0140 1 0.576 0.576 0.029976
3 0.0095 3 0.548 0.578 0.030013
4 0.0070 7 0.510 0.552 0.029517
5 0.0050 9 0.496 0.528 0.029035
6 0.0025 11 0.486 0.532 0.029117
7 0.0020 19 0.464 0.536 0.029198
8 0.0001 22 0.458 0.528 0.029035

ステップ 3: 木を剪定します。

次に、回帰ツリーを枝刈りして、テスト誤差を最小にする cp (複雑さのパラメーター) に使用する最適な値を見つけます。

cp の最適値は、前の出力で最小のx 誤差をもたらす値であることに注意してください。これは、相互検証データからの観測値の誤差を表します。

 #identify best cp value to use
best <- tree$cptable[which. min (tree$cptable[," xerror "])," CP "]

#produce a pruned tree based on the best cp value
pruned_tree <- prune (tree, cp=best)

#plot the pruned tree
prp(pruned_tree,
    faclen= 0 , #use full names for factor labels
    extra= 1 , #display number of obs. for each terminal node
    roundint= F , #don't round to integers in output
    digits= 5 ) #display 5 decimal places in output

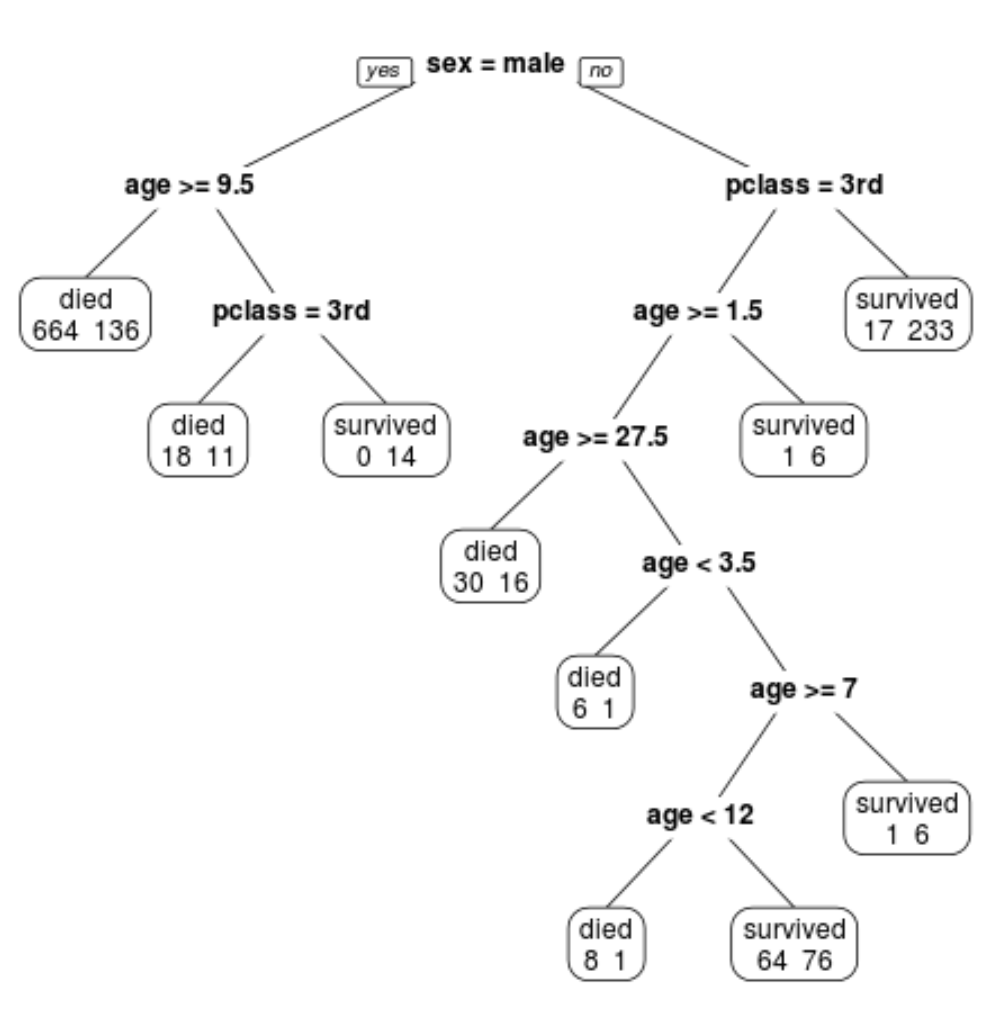
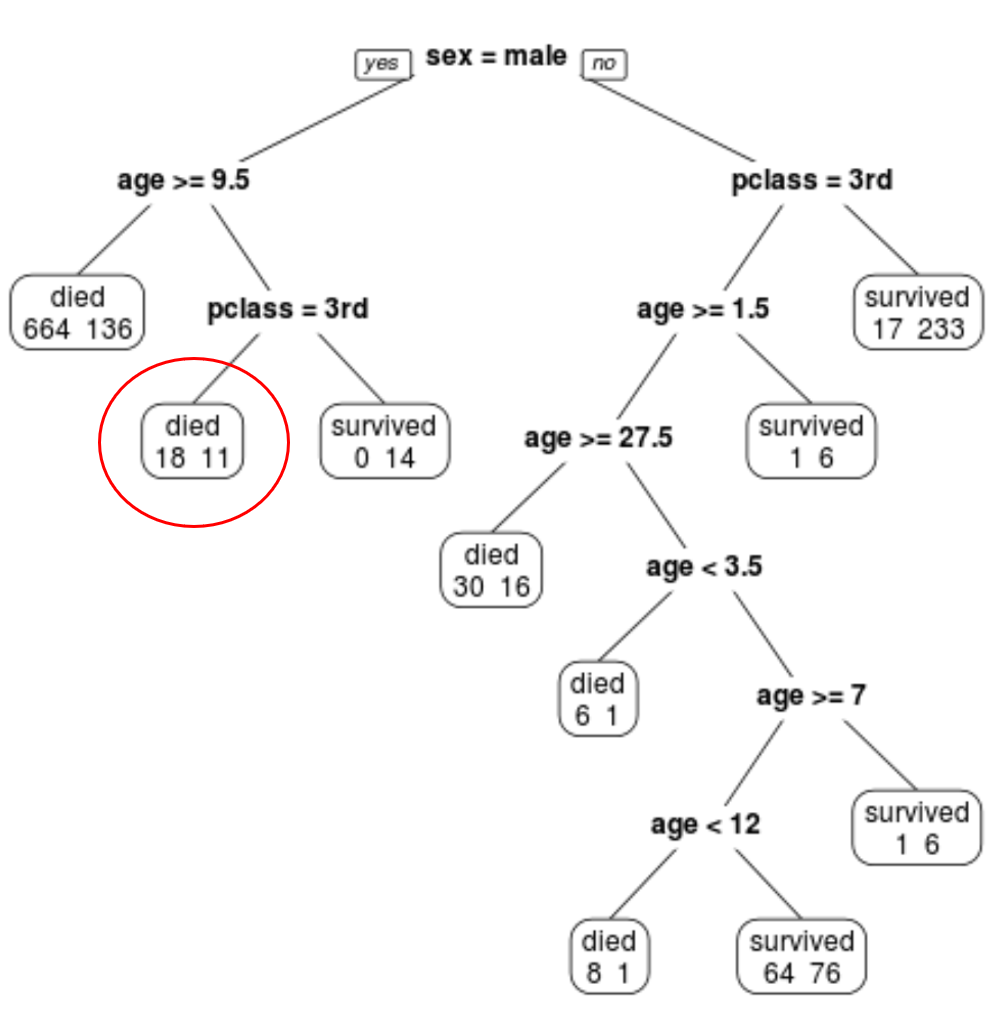
最終的に枝刈りされたツリーには 10 個の終端ノードがあることがわかります。各ターミナル ノードは、死亡した乗客の数と生存者の数を示します。

たとえば、一番左のノードでは、664 人の乗客が死亡し、136 人が生き残ったことがわかります。

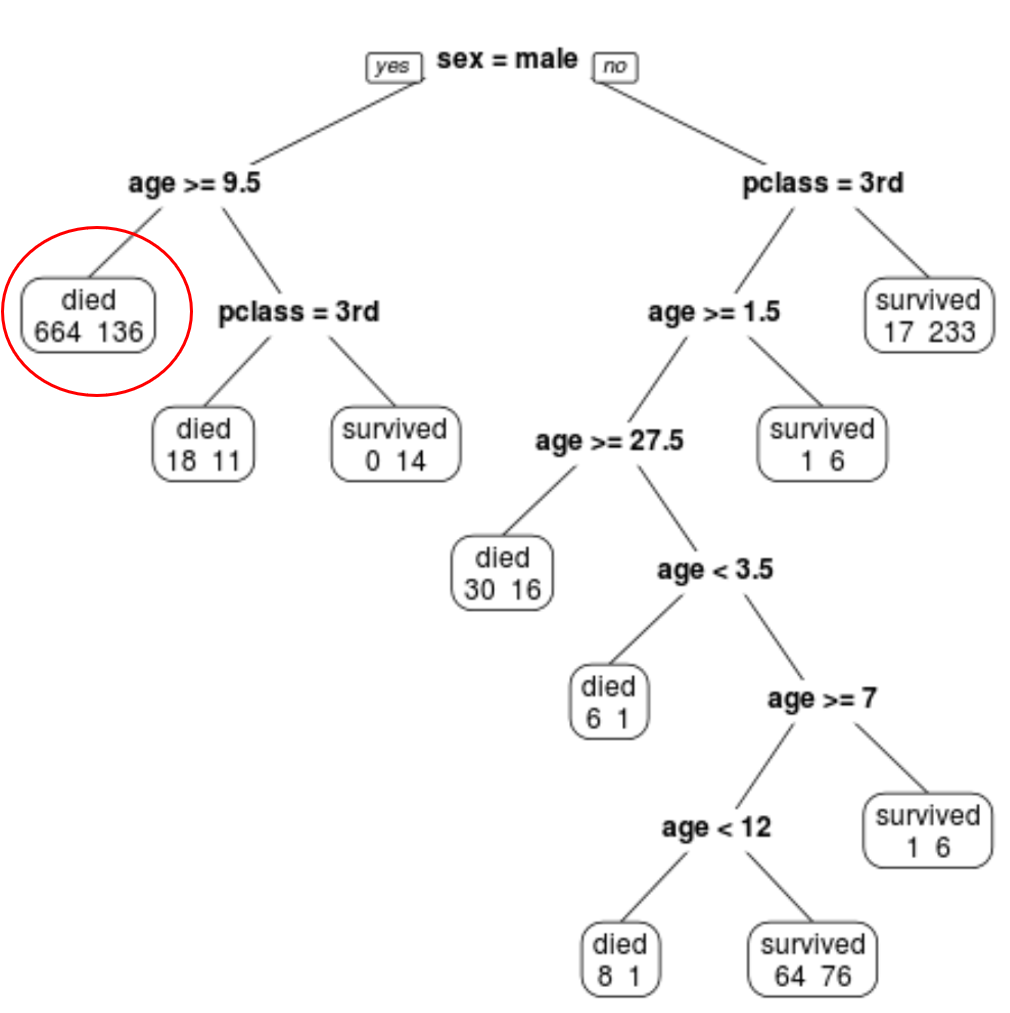
ステップ 4: ツリーを使用して予測を行います。

最終的に剪定された木を使用して、クラス、年齢、性別に基づいて特定の乗客が生き残る確率を予測できます。

たとえば、1 クラスの 8 歳の男性乗客の生存確率は 11/29 = 37.9% です。

これらの例で使用されている完全な R コードは、ここで見つけることができます。