R で加重最小二乗回帰を実行する方法
線形回帰の重要な前提の 1 つは、予測変数の各レベルで残差が等しい分散で分布しているということです。この仮定は等分散性として知られています。
この仮定が尊重されない場合、残差に不均一分散性が存在すると言われます。これが起こると、回帰結果は信頼できなくなります。
この問題を解決する 1 つの方法は、重み付き最小二乗回帰を使用することです。これは、誤差分散が小さい観測値には、より大きな誤差分散を持つ観測値と比較してより多くの情報が含まれるため、より多くの重みを受け取るように観測値に重みを割り当てます。
このチュートリアルでは、R で重み付き最小二乗回帰を実行する方法の段階的な例を示します。
ステップ 1: データを作成する
次のコードは、16 人の学生の学習時間数と対応する試験のスコアを含むデータ フレームを作成します。
df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))
ステップ 2: 線形回帰を実行する
次に、 lm()関数を使用して、予測変数として時間を使用し、応答変数としてスコアを使用する単純な線形回帰モデルを近似します。
#fit simple linear regression model model <- lm(score ~ hours, data = df) #view summary of model summary(model) Call: lm(formula = score ~ hours, data = df) Residuals: Min 1Q Median 3Q Max -17,967 -5,970 -0.719 7,531 15,032 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 60,467 5,128 11,791 1.17e-08 *** hours 5,500 1,127 4,879 0.000244 *** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 9.224 on 14 degrees of freedom Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438
ステップ 3: 不均一分散性をテストする
次に、残差と近似値のプロットを作成して、不均一分散性を視覚的に確認します。
#create residual vs. fitted plot plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ') #add a horizontal line at 0 abline(0,0)
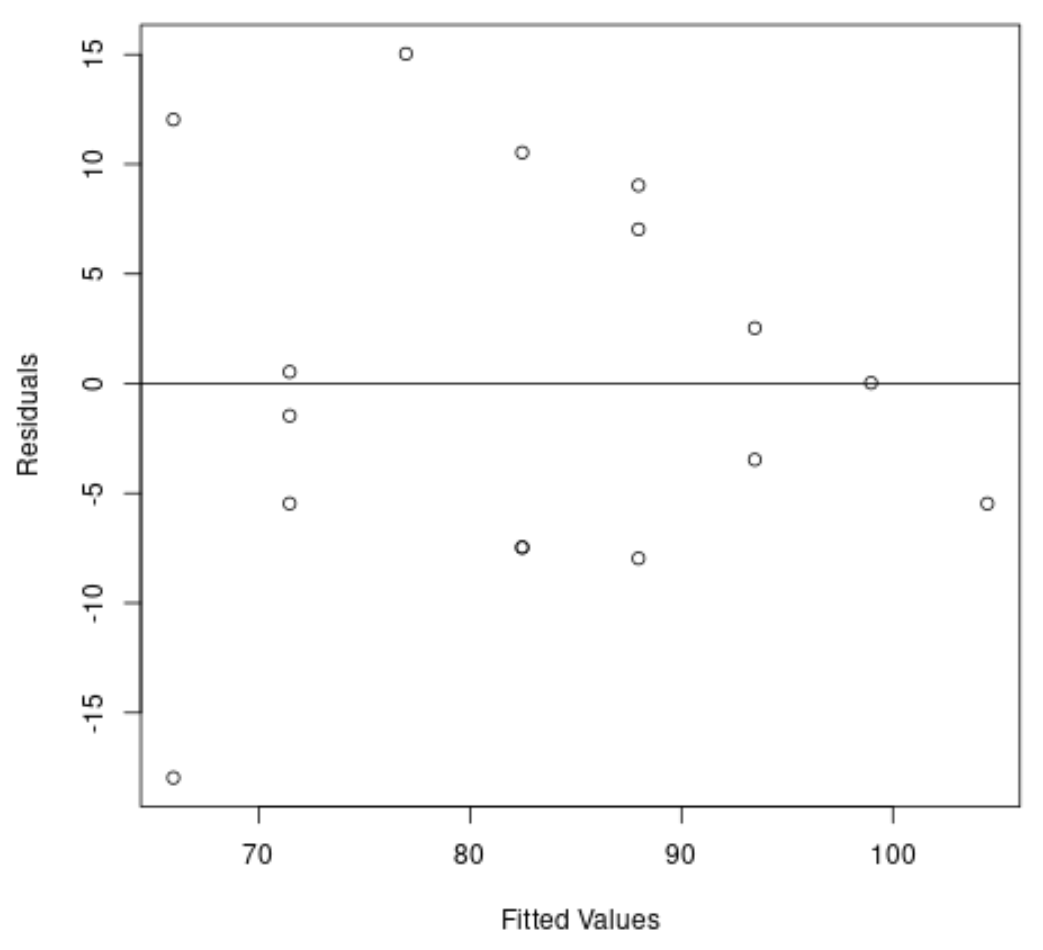
グラフから、残差が「円錐」の形状をしていることがわかります。残差はグラフ全体に均等な分散で分布しているわけではありません。
不均一分散性を正式にテストするには、Breusch-Pagan テストを実行できます。
#load lmtest package library (lmtest) #perform Breusch-Pagan test bptest(model) studentized Breusch-Pagan test data: model BP = 3.9597, df = 1, p-value = 0.0466
Breusch-Pagan 検定では、次の帰無仮説と対立仮説が使用されます。
- 帰無仮説 (H 0 ): 等分散性が存在します (残差は等分散で分布します)
- 対立仮説 ( HA ):不均一分散が存在します (残差は等分散で分布していません)
検定の p 値は0.0466であるため、帰無仮説を棄却し、このモデルでは不均一分散性が問題であると結論付けます。
ステップ 4: 加重最小二乗回帰を実行する
不均一分散性が存在するため、分散が小さい観測値がより多くの重みを受け取るように重みを設定して、重み付き最小二乗法を実行します。
#define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2
#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)
#view summary of model
summary(wls_model)
Call:
lm(formula = score ~ hours, data = df, weights = wt)
Weighted Residuals:
Min 1Q Median 3Q Max
-2.0167 -0.9263 -0.2589 0.9873 1.6977
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05
結果から、時間予測変数の係数推定値がわずかに変化し、全体的なモデルの適合性が向上したことがわかります。
加重最小二乗モデルの残差標準誤差は1.199ですが、元の単純線形回帰モデルの残差標準誤差は9.224です。
これは、重み付き最小二乗モデルによって生成された予測値が、単純な線形回帰モデルによって生成された予測値と比較して、実際の観測値にはるかに近いことを示しています。
加重最小二乗モデルの R 二乗も0.6762ですが、元の単純線形回帰モデルの R 二乗は0.6296です。
これは、加重最小二乗モデルの方が、単純な線形回帰モデルよりも試験得点の分散をより多く説明できることを示しています。
これらの測定値は、単純な線形回帰モデルと比較して、加重最小二乗モデルの方がデータへの適合性が高いことを示しています。