R で指数分布をプロットする方法

指数分布は、特定のイベントが発生するまで待機する時間をモデル化するために使用される確率分布です。

確率変数X が指数分布に従う場合、 Xの確率密度関数は次のように書くことができます。

f (x; λ) = λe ^-λx

金：

• λ:レートパラメータ
• e: 2.718 にほぼ等しい定数

の累積分布関数

F (x; λ) = 1 – e ^-λx

このチュートリアルでは、R で指数分布の PDF および CDF をプロットする方法について説明します。

確率密度関数のプロット

次のコードは、レート パラメーター λ = 0.5 を使用して指数分布の PDF をプロットする方法を示しています。

 curve ( dexp (x, rate = .5), from=0, to=10, col=' blue ')

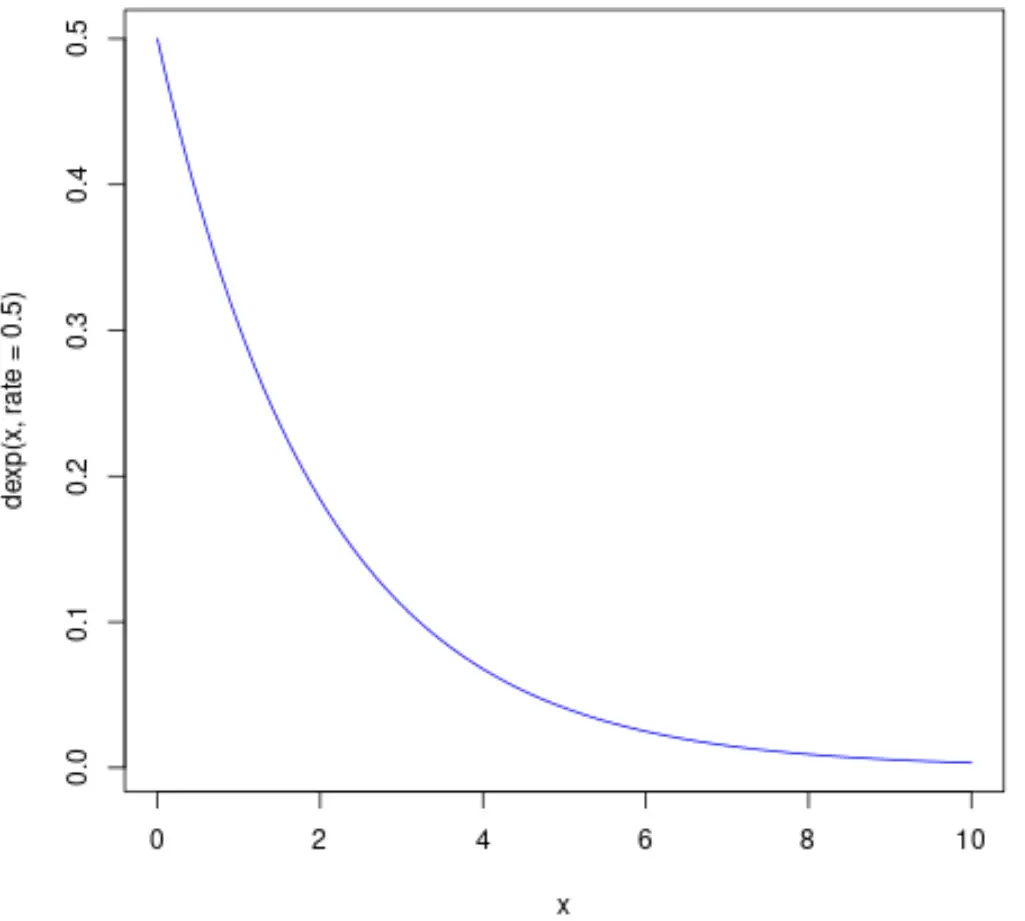
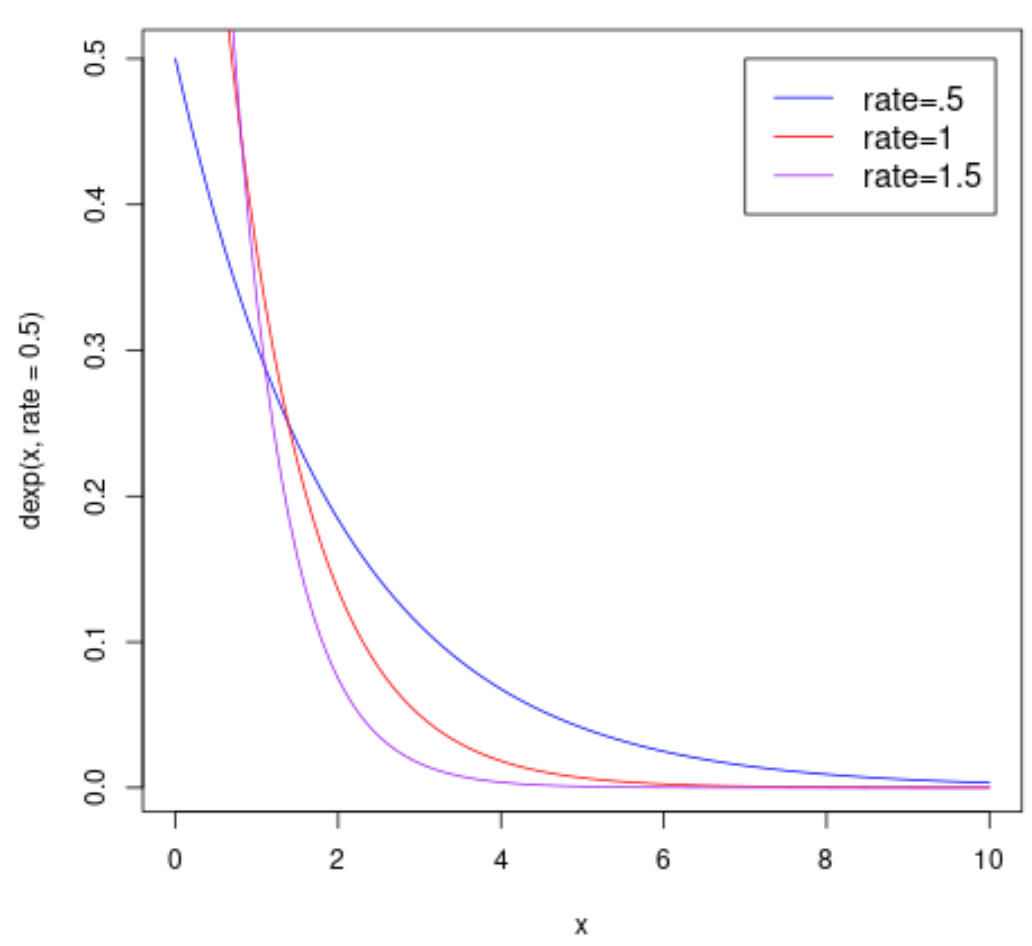
次のコードは、異なるレート パラメーターを使用して指数分布の複数の PDF をプロットする方法を示しています。

 #plot PDF curves
curve ( dexp (x, rate = .5), from=0, to=10, col=' blue ')
curve ( dexp (x, rate = 1), from=0, to=10, col=' red ', add= TRUE )
curve ( dexp (x, rate = 1.5), from=0, to=10, col=' purple ', add= TRUE )

#add legend
legend (7, .5, legend=c(" rate=.5 ", " rate=1 ", " rate=1.5 "),
       col=c(" blue ", " red ", " purple "), lty=1, cex=1.2)

累積分布関数のプロット

次のコードは、レート パラメーター λ = 0.5 を使用して指数分布の CDF をプロットする方法を示しています。

 curve ( pexp (x, rate = .5), from=0, to=10, col=' blue ') 

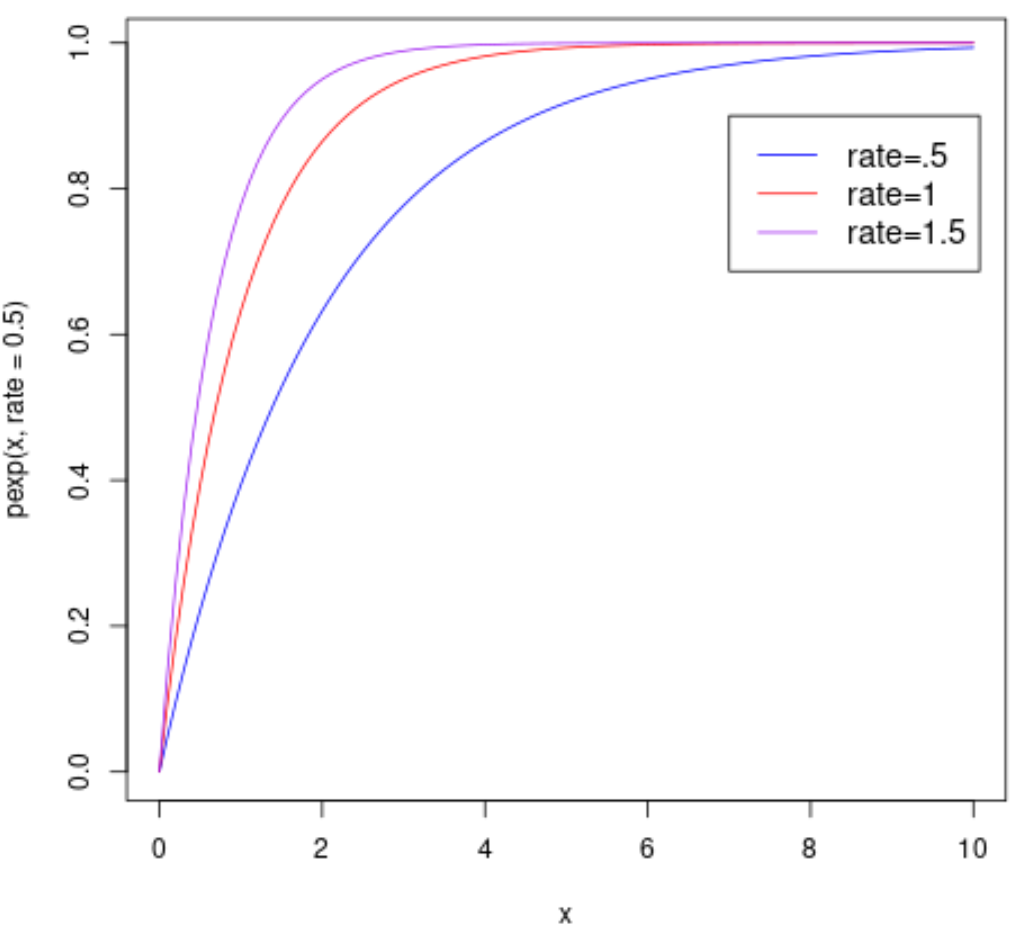
次のコードは、異なるレート パラメーターを使用して指数分布の複数の CDF をプロットする方法を示しています。

 #plot CDF curves
curve ( pexp (x, rate = .5), from=0, to=10, col=' blue ')
curve ( pexp (x, rate = 1), from=0, to=10, col=' red ', add= TRUE )
curve ( pexp (x, rate = 1.5), from=0, to=10, col=' purple ', add= TRUE )

#add legend
legend (7, .9, legend=c(" rate=.5 ", " rate=1 ", " rate=1.5 "),
       col=c(" blue ", " red ", " purple "), lty=1, cex=1.2) 

追加リソース

次のチュートリアルでは、R で他の確率分布をプロットする方法を説明します。

R でポアソン分布をプロットする方法
R で二項分布をプロットする方法
R で分布にプロットする方法
R で正規分布をプロットする方法
R でカイ二乗分布をプロットする方法