R の指数回帰 (ステップバイステップ)

指数回帰は、次の状況をモデル化するために使用できる回帰の一種です。

1. 指数関数的成長:成長はゆっくりと始まり、その後急速に無制限に加速します。

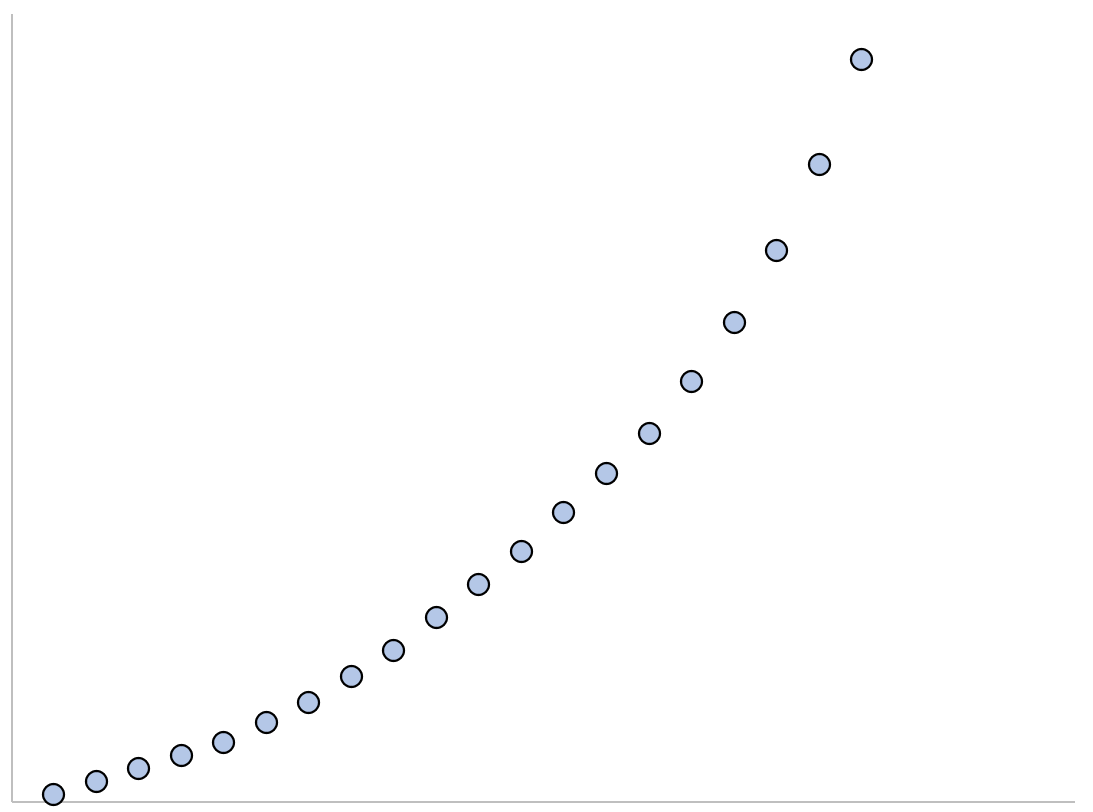
2. 指数関数的減衰:減衰は急速に始まり、徐々にゼロに近づいて減速します。

指数回帰モデルの方程式は次の形式になります。

y = 絶対^x

金：

• y:応答変数
• x:予測変数
• a、b: xとyの関係を説明する回帰係数

次の段階的な例は、R で指数回帰を実行する方法を示しています。

ステップ 1: データを作成する

まず、2 つの変数xとyの偽のデータを作成しましょう。

 x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

ステップ 2: データを視覚化する

次に、簡単な散布図を作成して、 xとyの関係を視覚化しましょう。

 plot(x, y) 

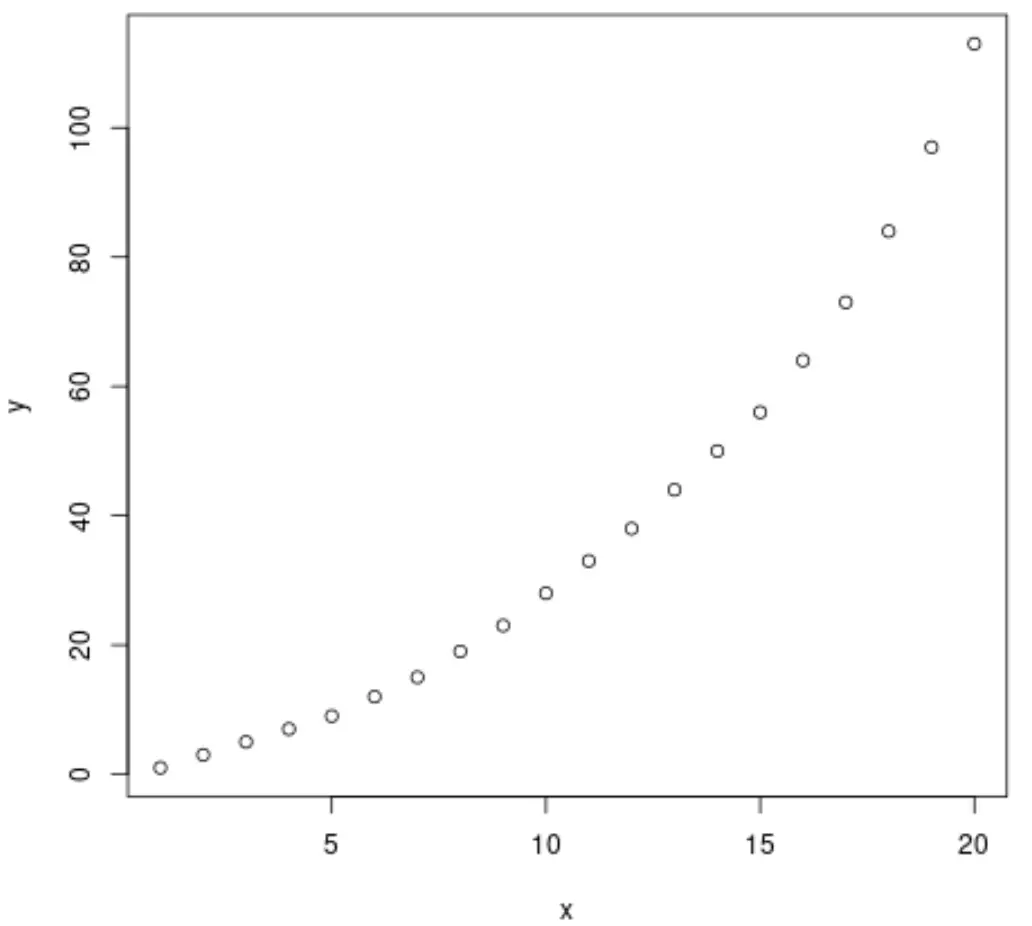
グラフから、2 つの変数間に明確な指数関数的な増加パターンがあることがわかります。

したがって、指数回帰式を当てはめて変数間の関係を説明することが賢明であると思われます。

ステップ 3: 指数回帰モデルを当てはめる

次に、 lm()関数を使用して、 yの自然対数を応答変数として、 x を予測変数として使用して、指数回帰モデルを近似します。

 #fit the model
model <- lm( log (y) ~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min 1Q Median 3Q Max 
-1.1858 -0.1768 0.1104 0.2720 0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.98166 0.17118 5.735 1.95e-05 ***
x 0.20410 0.01429 14.283 2.92e-11 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11

モデル全体の F 値は 204 で、対応する p 値は非常に低く (2.917e-11)、モデル全体が有用であることを示しています。

出力テーブルの係数を使用すると、近似された指数回帰式が次のようになることがわかります。

ln(y) = 0.9817 + 0.2041(x)

eを両辺に適用すると、方程式を次のように書き換えることができます。

y = 2.6689 * ^1.2264x

この方程式を使用して、予測子変数xの値に基づいて応答変数yを予測できます。たとえば、 x = 12 の場合、 y は30.897になると予測します。

y = 2.6689 * 1.2264 ¹² = 30.897

ボーナス:このオンライン指数回帰計算ツールを自由に使用して、指定された予測変数と応答変数の指数回帰式を自動的に計算できます。

追加リソース

R で単純な線形回帰を実行する方法
R で重回帰を実行する方法
R で二次回帰を実行する方法
R で多項式回帰を実行する方法