R で複数の変数間の相関を計算する方法

2 つの変数間の関係を定量化する 1 つの方法は、2 つの変数間の線形関連性の尺度であるピアソン相関係数を使用することです。常に -1 から 1 までの値を取ります。

• -1 は、2 つの変数間の完全な負の線形相関を示します。
• 0 は 2 つの変数間に線形相関がないことを示します
• 1 は、2 つの変数間の完全な正の線形相関を示します。

このチュートリアルでは、次のデータ フレームを例として、R で複数の変数間の相関関係を計算する方法を説明します。

 #create data frame
df <- data.frame(a <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23),
                 b <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43),
                 c <- c(13, 14, 14, 14, 15, 17, 18, 19, 22, 20, 24, 26),
                 d <- c(6, 6, 7, 8, 8, 8, 7, 6, 5, 3, 3, 2))

例 1: 2 つの変数間の相関関係

次のコードは、データ フレーム内の 2 つの変数間の相関関係を計算する方法を示しています。

 cor(df$a, df$b)

[1] 0.9279869

例 2: 複数の変数間の相関関係

次のコードは、データ フレーム内の 3 つの変数間の相関を計算する方法を示しています。

 cor(df[, c(' a ', ' b ', ' c ')])

          ABC
a 1.0000000 0.9279869 0.9604329
b 0.9279869 1.0000000 0.8942139
c 0.9604329 0.8942139 1.0000000

結果を解釈する方法は次のとおりです。

• aとbの相関は 0.9279869 です。
• aとcの相関は 0.9604329 です。
• bとcの相関は 0.8942139 です。

例 3: すべての変数間の相関

次のコードは、データ フレーム内のすべての変数間の相関を計算する方法を示しています。

 cor(df)

           abcd
a 1.0000000 0.9279869 0.9604329 -0.7915488
b 0.9279869 1.0000000 0.8942139 -0.7917973
c 0.9604329 0.8942139 1.0000000 -0.8063549
d -0.7915488 -0.7917973 -0.8063549 1.0000000

例 4: 数値変数のみ間の相関

次のコードは、データ フレーム内の数値変数のみの間の相関を計算する方法を示しています。

 cor(df[, unlist ( lapply (df, is. numeric ))])

           abcd
a 1.0000000 0.9279869 0.9604329 -0.7915488
b 0.9279869 1.0000000 0.8942139 -0.7917973
c 0.9604329 0.8942139 1.0000000 -0.8063549
d -0.7915488 -0.7917973 -0.8063549 1.0000000

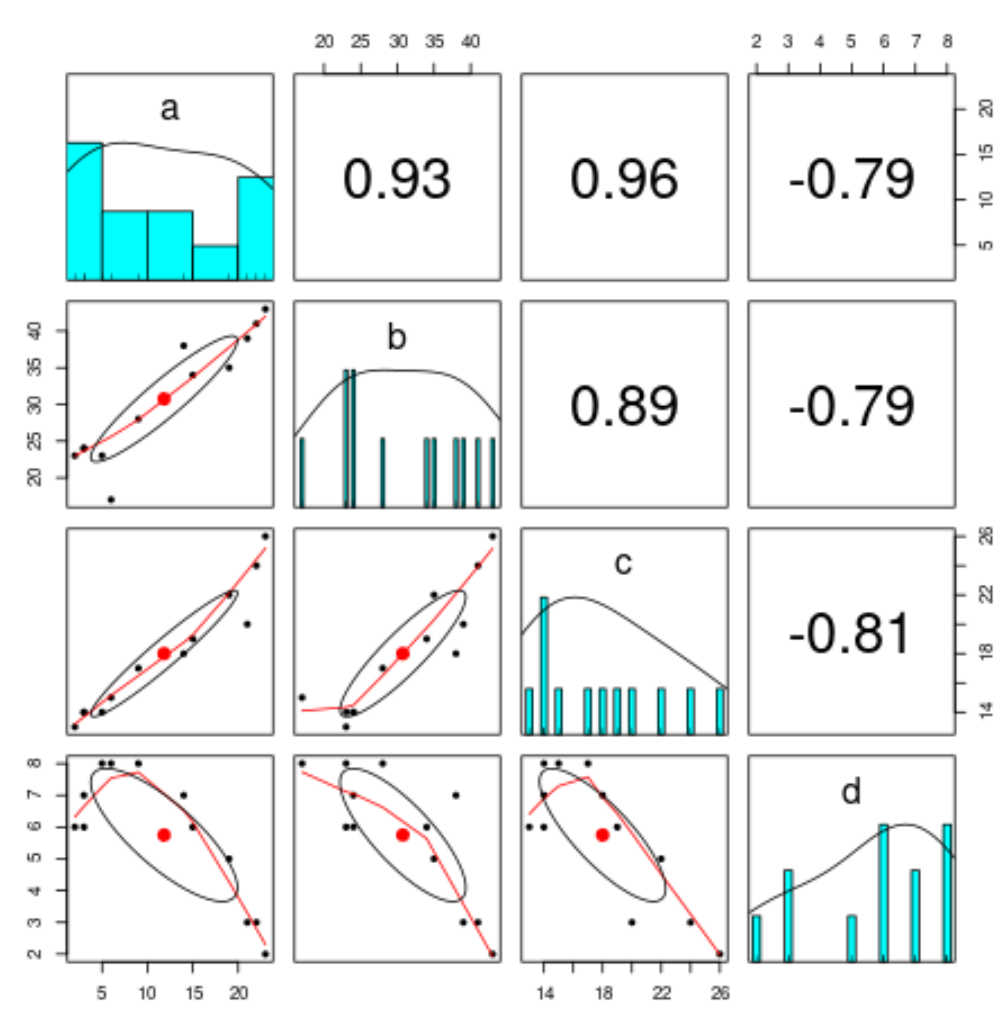
例 5: 相関関係の視覚化

次のコードは、ペアごとのプロット (変数のペアごとの組み合わせ間の関係を視覚化できるタイプのプロット) を作成する方法を示しています。

 #load psych package
library(psych)

#create pairs plot
peers. panels (df)

追加リソース

R で偏相関を計算する方法
R で点双系列相関を計算する方法
R でスライド相関を計算する方法