R で診断プロットを解釈する方法

線形回帰モデルは、1 つ以上の予測変数と応答変数の間の関係を記述するために使用されます。

ただし、回帰モデルを当てはめたら、診断プロットも作成してモデルの残差を分析し、作業している特定のデータに線形モデルが適切に使用できるかどうかを確認することをお勧めします。

このチュートリアルでは、R で特定の回帰モデルの診断プロットを作成および解釈する方法について説明します。

例: R で診断プロットを作成および解釈する

「学習時間」を使用して単純な線形回帰モデルを当てはめて、特定のクラスの生徒の「試験の成績」を予測するとします。

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

Lot()コマンドを使用すると、この回帰モデルの 4 つの診断プロットを作成できます。

 #produce diagnostic plots for regression model
plot(model)

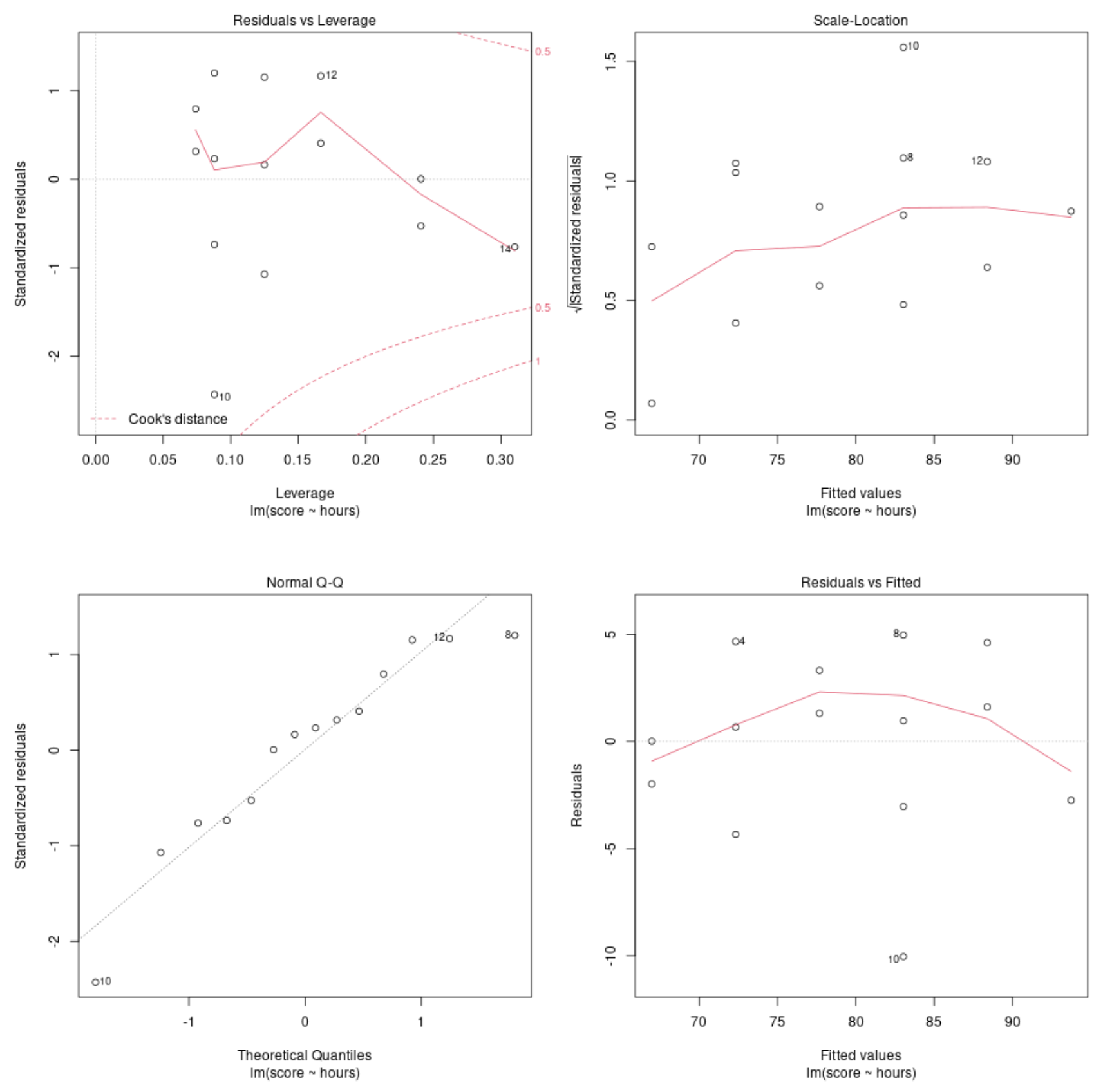
診断チャート #1: 残差 vs.レバレッジチャート

このグラフは、影響力のある観測値を特定するために使用されます。このグラフ上の点がクックの距離 (点線) の外にある場合、これは影響力のある観測値です。

この例では、観測 #10 がクック距離制限に最も近いですが、点線の外には出ていないことがわかります。これは、データセット内に過度に影響を与えるポイントがないことを意味します。

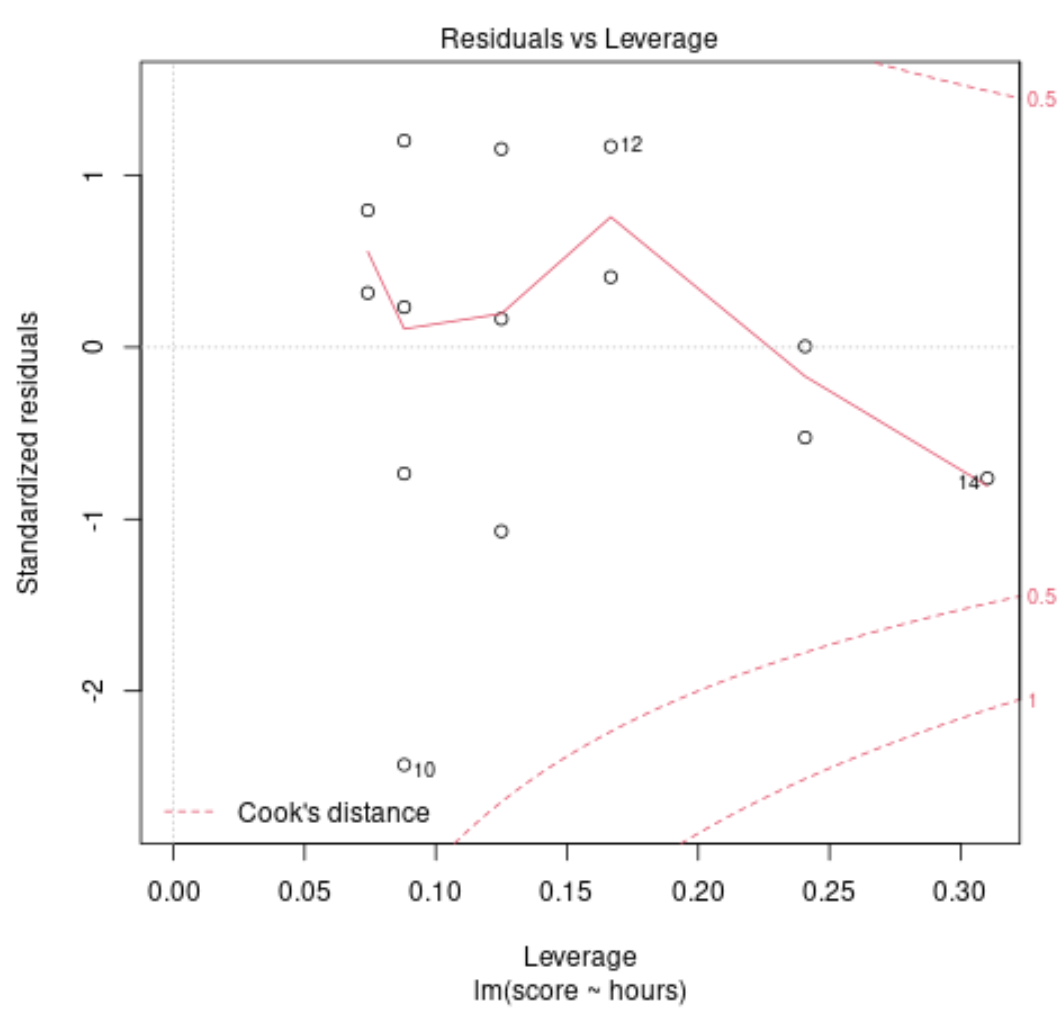
診断プロット #2: スケールと位置のプロット

このグラフは、回帰モデルの残差間の分散の等価性 (「等分散性」とも呼ばれる) の仮定を検証するために使用されます。赤い線がプロット上でほぼ水平である場合は、等分散の仮定が満たされている可能性があります。

この例では、赤い線がプロット上で正確に水平ではありませんが、どの点でも大きく逸脱していないことがわかります。この場合、等分散の仮定は破られていないとおそらく言えます。

関連:回帰分析における不均一分散性の理解

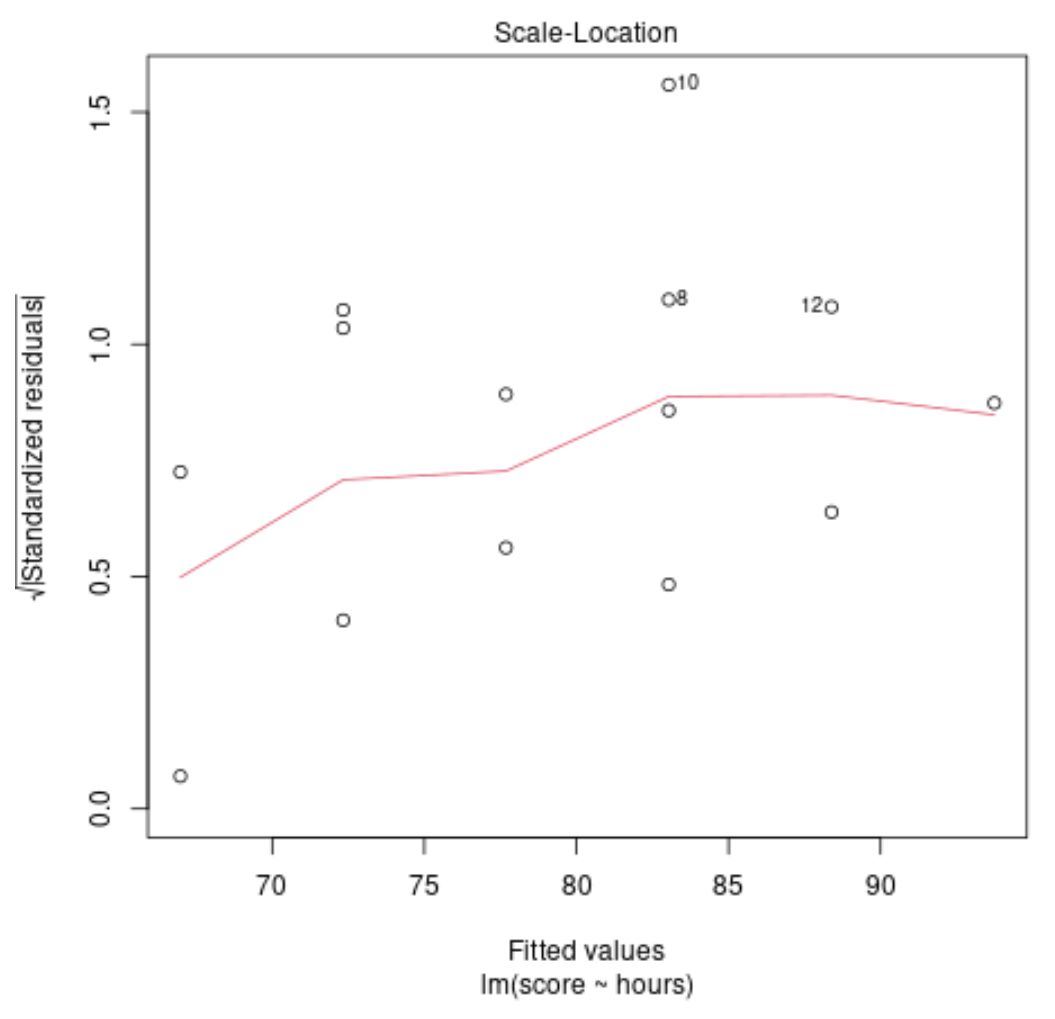
診断トレース #3: 通常の QQ トレース

このプロットは、回帰モデルからの残差が正規分布しているかどうかを判断するために使用されます。このグラフ上の点がほぼ直線の対角線に沿って配置されている場合、残差は正規分布していると仮定できます。

この例では、点がほぼ対角線の直線に沿って配置されていることがわかります。観測値 #10 と #8 は端の線から少し外れていますが、残差が正規分布ではないと宣言するには十分ではありません。

診断プロット #4: 残差 vs.調整されたプロット

このプロットは、残差が非線形パターンを示すかどうかを判断するために使用されます。プロットの中央の赤い線がほぼ水平である場合、残差は線形パターンに従っていると想定できます。

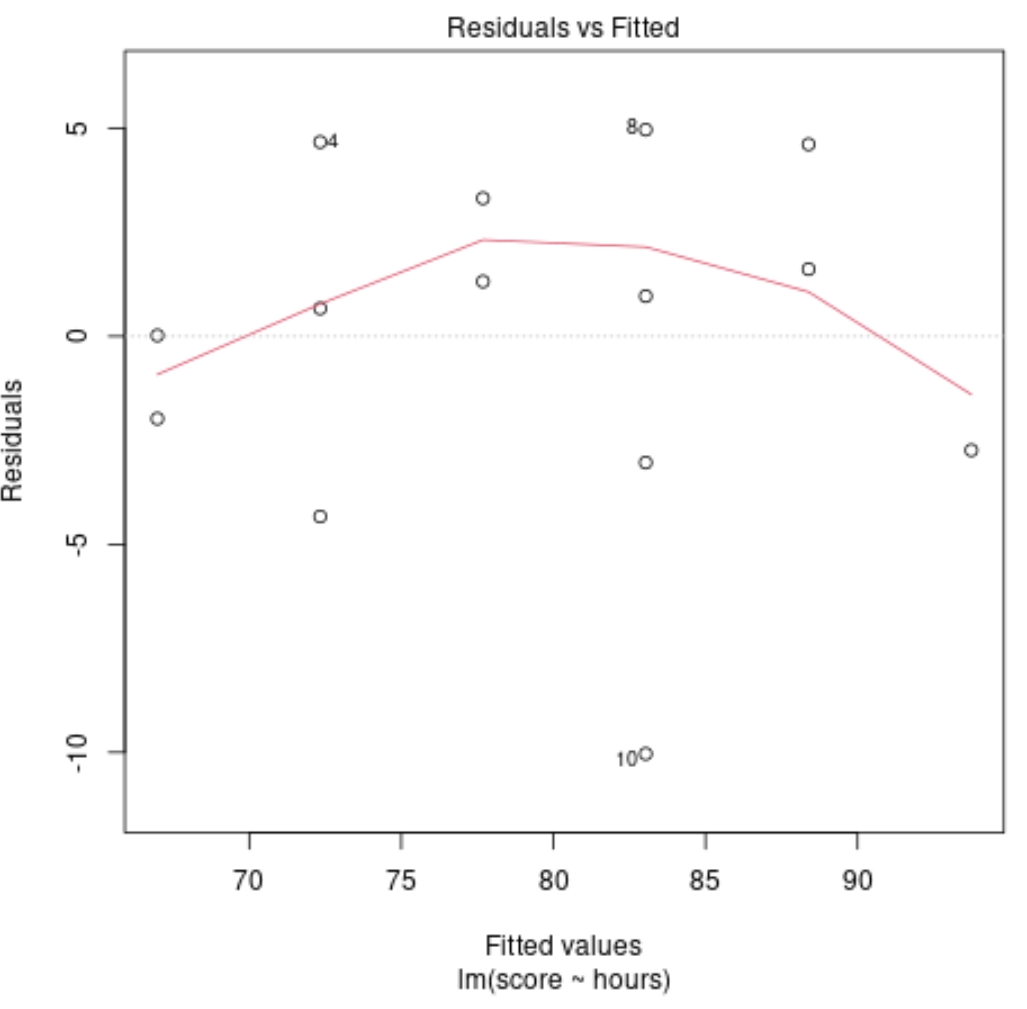
この例では、赤い線が完全な水平線から逸脱していますが、大きくは逸脱していないことがわかります。おそらく、残差はほぼ線形のパターンに従い、このデータセットには線形回帰モデルが適切であると考えられます。

追加リソース

線形回帰の 4 つの仮定
統計における残差とは何ですか?
R で残差プロットを作成する方法
縮尺と位置のプロットを解釈する方法