R で部分残差プロットを作成する方法
重線形回帰は、複数の予測変数と応答変数の間の関係を理解するために使用できる統計手法です。
ただし、重線形回帰の重要な前提の 1 つは、各予測変数と応答変数の間に線形関係があるということです。
この仮定が満たされない場合、回帰モデルの結果は信頼できない可能性があります。
この仮定をテストする 1 つの方法は、応答変数に対する予測子変数の残差を表示する部分残差プロットを作成することです。
次の例は、R で回帰モデルの部分残差プロットを作成する方法を示しています。
例: R で部分残差プロットを作成する方法
R の 3 つの予測子変数を使用して回帰モデルを近似するとします。
#make this example reproducible set. seeds (0) #define response variable y <- c(1:1000) #define three predictor variables x1 <- c(1:1000)*runif(n=1000) x2 <- (c(1:1000)*rnorm(n=1000))^2 x3 <- (c(1:1000)*rnorm(n=1000))^3 #fit multiple linear regression model model <- lm(y~x1+x2+x3))
R のcarパッケージのcrPlots()関数を使用して、モデル内の各予測子変数の部分残差プロットを作成できます。
library (car) #create partial residual plots crPlots(model)
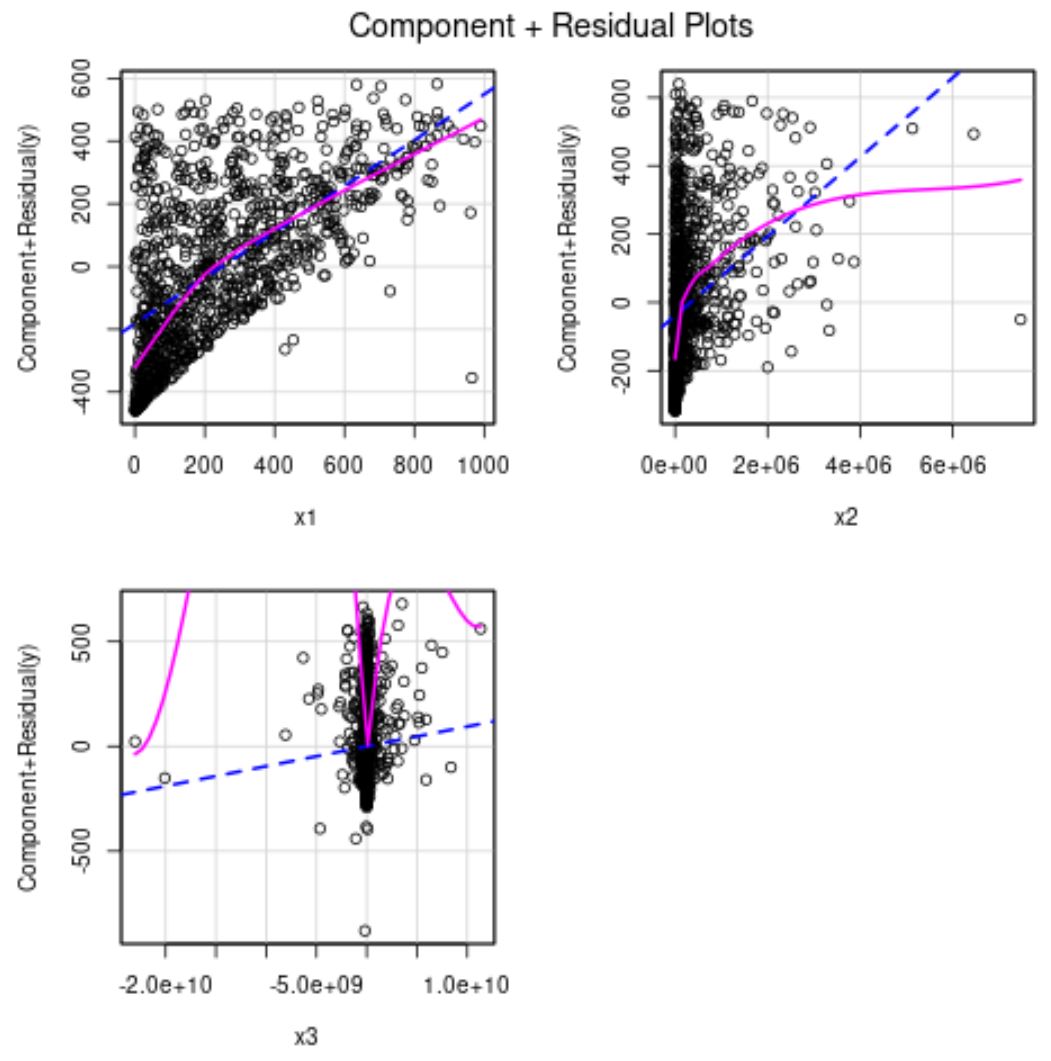
青い線は、予測変数と応答変数の間の関係が線形である場合に期待される残差を示します。ピンクの線は実際の残差を示します。
2 つの線が大きく異なる場合、これは非線形関係を示します。
上のグラフから、x2 と x3 の残差が非線形であることがわかります。
これは、重回帰の線形性の仮定に違反します。この問題を解決する 1 つの方法は、予測子変数に対して平方根または立方根変換を使用することです。
library (car) #fit new model with transformed predictor variables model_transformed <- lm(y~x1+sqrt(x2)+log10(x3^(1/3))) #create partial residual plots for new model crPlots(model_transformed)
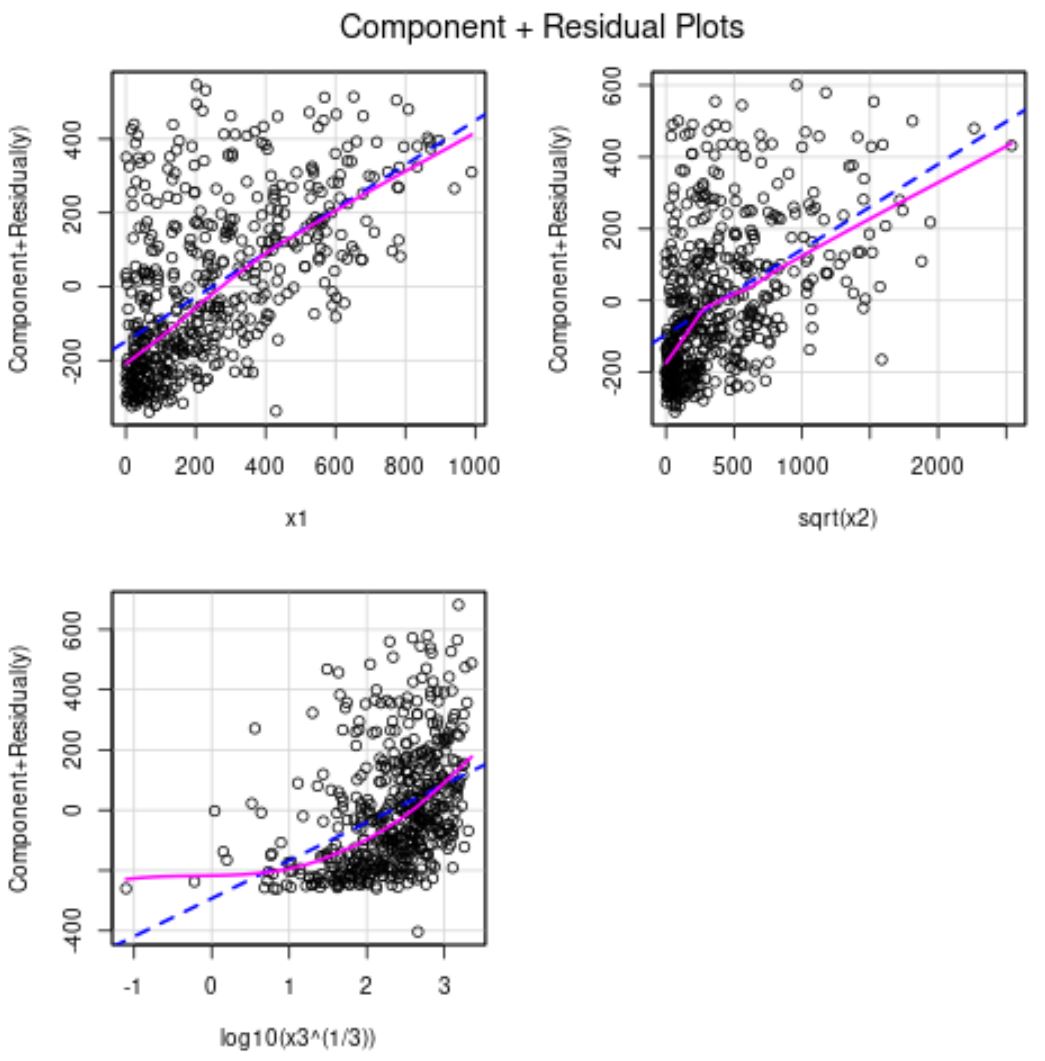
部分残差プロットから、x2 が応答変数とより線形な関係になっていることがわかります。
x3 予測子変数はまだいくらか非線形であるため、別の変換を試みるか、場合によってはモデルから変数を完全に削除することを決定する場合があります。
追加リソース
次のチュートリアルでは、R で他の一般的なプロットを作成する方法を説明します。