R でボックス-コックス変換を実行する方法 (例付き)

ボックス コックス変換は、非正規分布のデータ セットをより正規分布のセットに変換するために一般的に使用される方法です。

この方法の基本的な考え方は、次の式を使用して、変換されたデータができるだけ正規分布に近づくような λ の値を見つけることです。

• y(λ) = (y ^λ – 1) / λ (y ≠ 0 の場合)
• y = 0の場合、y(λ) = log(y)

MASS()ライブラリのboxcox()関数を使用して、R で box-cox 変換を実行できます。次の例は、この関数を実際に使用する方法を示しています。

Box-Cox 変換の開発に関する優れた概要については、コネチカット大学のこの記事を参照してください。

例: R でのボックス-コックス変換

次のコードは、線形回帰モデルをデータセットに近似し、 boxcox()関数を使用して最適なラムダを見つけて応答変数を変換し、新しいモデルを近似する方法を示しています。

 library (MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

最適なラムダは-0.4242424であることが判明しました。したがって、新しい回帰モデルは、元の応答変数 y を変数 y = (y ^-0.4242424 – 1) / -0.4242424 に置き換えました。

次のコードは、R で 2 つのQQ プロットを作成し、2 つの回帰モデル間の残差の違いを視覚化する方法を示しています。

 #define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#QQ plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#QQ plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both QQ plots
by(op)

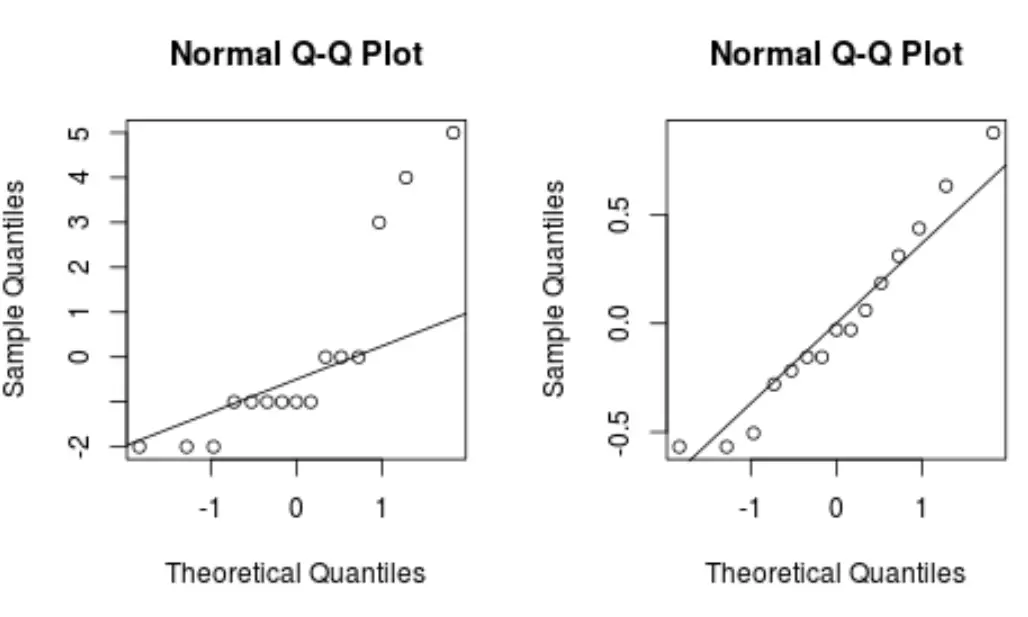
一般に、データ ポイントが QQ プロットの直線の対角線に沿って配置されている場合、データ セットは正規分布に従う可能性があります。

ボックスコックス変換モデルが元の回帰モデルよりもはるかに直線的な QQ プロットを生成することに注目してください。

これは、ボックス-コックス変換モデルの残差がより正規分布しており、 線形回帰の仮定の 1 つを満たしていることを示しています。

追加リソース

R でデータを変換する方法 (対数、平方根、立方根)
R で QQ プロットを作成して解釈する方法
R で正規性について Shapiro-Wilk テストを実行する方法