二乗平均平方根誤差 (rmse) を解釈する方法

回帰分析は、1 つ以上の予測変数と応答変数の間の関係を理解するために使用できる手法です。

回帰モデルがデータセットにどの程度適合しているかを評価する 1 つの方法は、平均二乗誤差を計算することです。これは、モデルの予測値とデータセットの実際の値の間の平均距離を示す指標です。

RMSE が低いほど、特定のモデルはデータセットに「適合」できます。

平均二乗誤差を求める公式 ( RMSEと略されることがよくあります) は次のとおりです。

RMSE = √ Σ(P _i – O _i ) ² / n

金：

• Σは「和」を意味する派手な記号です
• Pi_は、データセット内の^{i 番目}の観測値の予測値です。
• O _iは、データセット内の^{i 番目}の観測値の観測値です。
• n はサンプルサイズです

次の例は、特定の回帰モデルの RMSE を解釈する方法を示しています。

例: 回帰モデルの RMSE を解釈する方法

「学習時間」を使用して、特定の大学入学試験における学生の「試験成績」を予測する回帰モデルを構築したいとします。

15 人の生徒について次のデータを収集します。

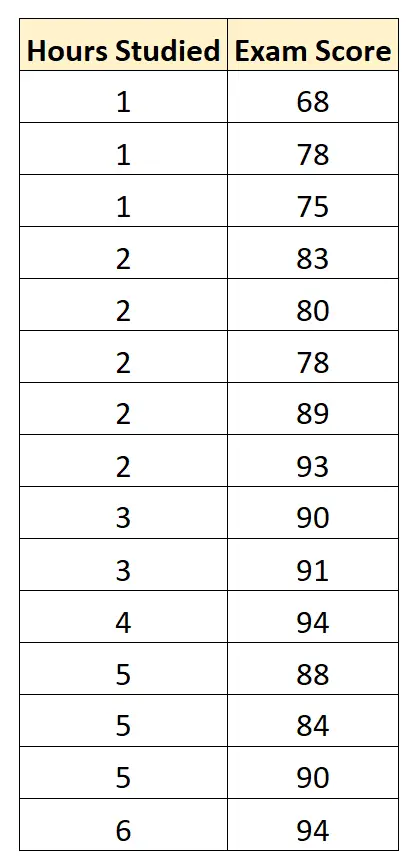
次に、統計ソフトウェア (Excel、SPSS、R、Python など) などを使用します。次の近似回帰モデルを見つけます。

試験のスコア = 75.95 + 3.08* (勉強時間)

次に、この方程式を使用して、各生徒の勉強時間数に基づいて各生徒の試験の得点を予測できます。

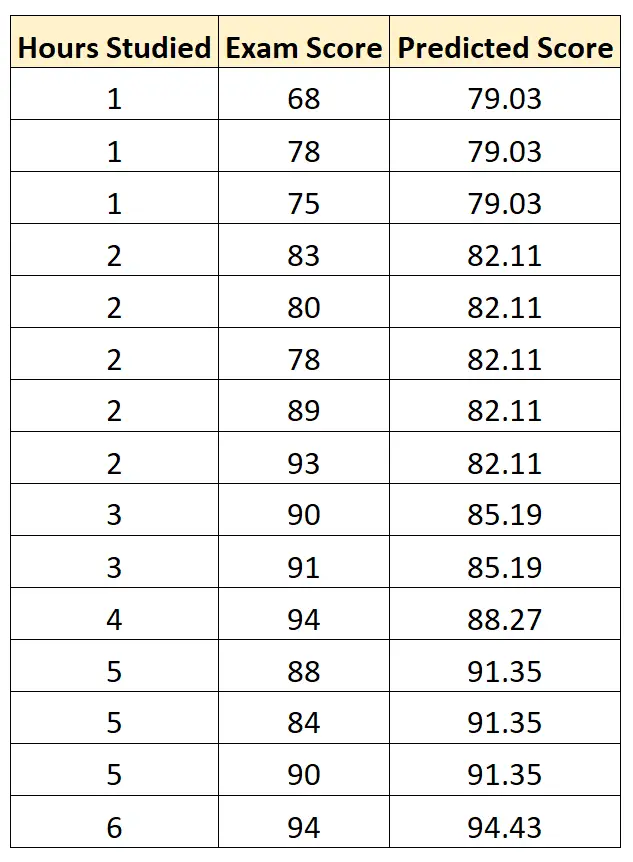
次に、各予測された試験スコアと実際の試験スコアの間の二乗差を計算できます。次に、これらの差の平均の平方根を求めることができます。

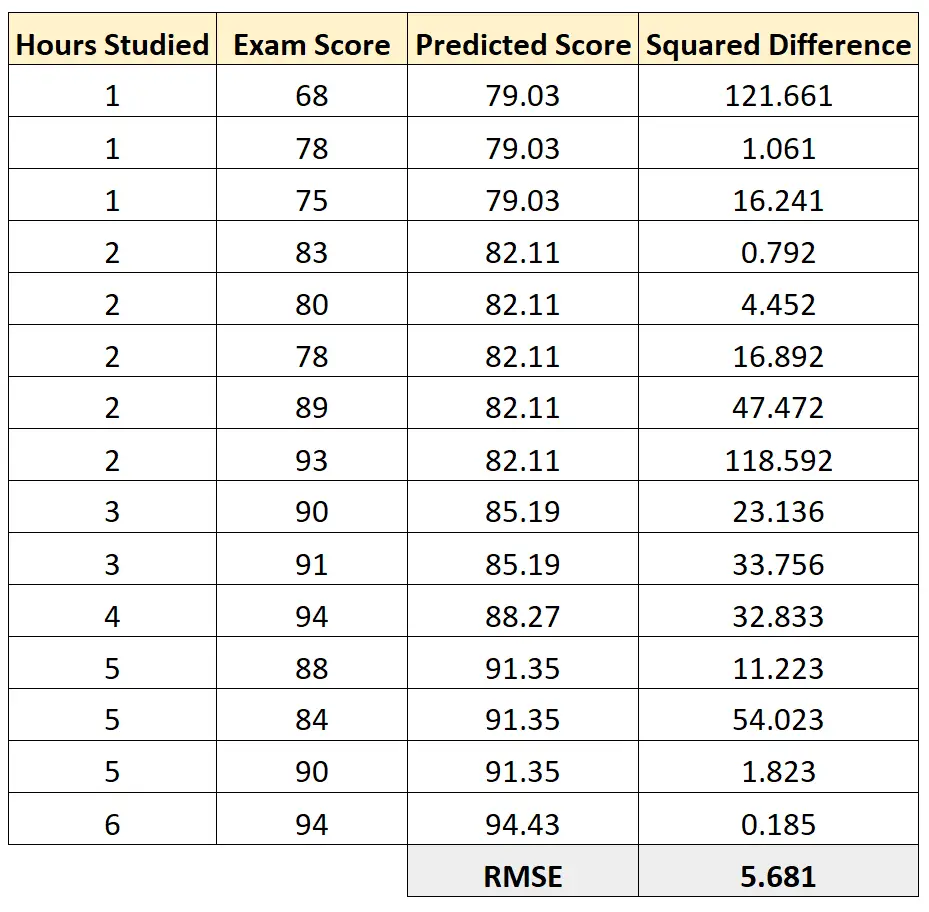
この回帰モデルの RMSE は5.681であることがわかります。

回帰モデルの残差は、観察されたデータ値とモデルの予測値の差であることを思い出してください。

残差= (P _i – O _i )

金

• Pi_は、データセット内の^{i 番目}の観測値の予測値です。
• O _iは、データセット内の^{i 番目}の観測値の観測値です。

また、回帰モデルの RMSE は次のように計算されることに注意してください。

RMSE = √ Σ(P _i – O _i ) ² / n

これは、 RMSE が残差の分散の平方根を表すことを意味します。

これは、観測されたデータ値と予測されたデータ値の間の平均距離を知ることができるため、知っておくと便利です。

これは、応答変数の分散のどの程度がモデルの予測変数によって説明できるかを示すモデルのR 二乗とは対照的です。

各種機種のRMSE値の比較

RMSE は、さまざまな回帰モデルの適合を比較する場合に特に役立ちます。

たとえば、学生の試験の得点を予測する回帰モデルを構築し、いくつかの潜在的なモデルの中から可能な限り最良のモデルを見つけたいとします。

3 つの異なる回帰モデルを当てはめて、対応する RMSE 値を見つけたとします。

• モデル1のRMSE： 14.5
• モデル2のRMSE： 16.7
• モデル3のRMSE： 9.8

モデル 3 の RMSE は最も低く、これは、3 つの潜在的なモデルの中で最もデータセットに適合できることを示しています。

追加リソース

RMSE計算機
Excel で RMSE を計算する方法
R で RMSE を計算する方法
Python で RMSE を計算する方法