R のファイ係数を計算する方法

ファイ係数(平均二乗分割係数と呼ばれることもあります) は、2 つのバイナリ変数間の関連性の尺度です。

2 つの確率変数xとyに対して与えられた 2×2 テーブルの場合:

ファイ係数は次のように計算できます。

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

例: R のファイ係数の計算

性別が政党の好みと関連しているかどうかを知りたいとします。そこで、25 人の有権者から 単純に無作為にサンプルを抽出し、政党の好みについて尋ねます。

次の表は、調査の結果を示しています。

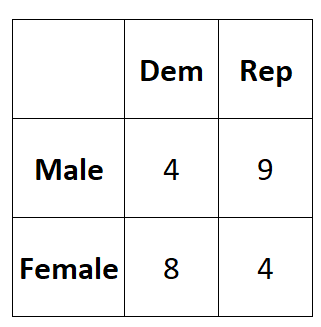
次のコードを使用して、このデータを R の 2×2 行列に入力できます。

 #create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2 )

#view dataset
data

     [,1] [,2]
[1,] 4 9
[2,] 8 4

次に、 psychパッケージのphi()関数を使用して、2 つの変数間のファイ係数を計算できます。

 #load psych package
library (psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

ファイ係数は-0.36であることがわかります。

phi 関数はデフォルトで 2 桁に丸められますが、必要な数の桁に丸めるように関数を指定できることに注意してください。

 #calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6 )

[1] -0.358974

ファイ係数の解釈方法

ピアソン相関係数と同様に、ファイ係数は -1 から 1 までの値を取ります。

• -1 は、 2 つの変数間の完全な負の関係を示します。
• 0 は、 2 つの変数間に関連性がないことを示します。
• 1 は、 2 つの変数間の完全な正の関係を示します。

一般に、ファイ係数がゼロから離れるほど、2 つの変数間の関係が強くなります。

言い換えれば、ファイ係数がゼロから遠ざかるほど、2 つの変数間に何らかの系統的なパターンがある証拠が多くなります。

追加リソース

ファイ係数の概要
ファイ係数計算機