R でレバレッジ統計を計算する方法
統計では、応答変数の値がデータセット内の残りの観測値よりもはるかに大きい観測値は外れ値とみなされます。
同様に、データセット内の残りの観測値と比較して非常に極端な予測変数の値が 1 つ以上ある観測値は、てこ比が高いと見なされます。
あらゆるタイプの分析における最初のステップの 1 つは、特定のモデルの結果に大きな影響を与える可能性があるため、高い影響力を持つ観測値を詳しく調べることです。
このチュートリアルでは、R のモデル内の各観測値のてこ比を計算して視覚化する方法を段階的に示します。
ステップ 1: 回帰モデルを作成する
まず、R に組み込まれているmtcarsデータセットを使用して重線形回帰モデルを作成します。
#load the dataset data(mtcars) #fit a regression model model <- lm(mpg~disp+hp, data=mtcars) #view model summary summary(model) Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 30.735904 1.331566 23.083 < 2nd-16 *** available -0.030346 0.007405 -4.098 0.000306 *** hp -0.024840 0.013385 -1.856 0.073679 . --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.127 on 29 degrees of freedom Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09
ステップ 2: 各観測値のてこ比を計算する
次に、 hatvalues()関数を使用して、モデル内の各観測値のてこ比を計算します。
#calculate leverage for each observation in the model hats <- as . data . frame (hatvalues(model)) #display leverage stats for each observation hats hatvalues(model) Mazda RX4 0.04235795 Mazda RX4 Wag 0.04235795 Datsun 710 0.06287776 Hornet 4 Drive 0.07614472 Hornet Sportabout 0.08097817 Valiant 0.05945972 Duster 360 0.09828955 Merc 240D 0.08816960 Merc 230 0.05102253 Merc 280 0.03990060 Merc 280C 0.03990060 Merc 450SE 0.03890159 Merc 450SL 0.03890159 Merc 450SLC 0.03890159 Cadillac Fleetwood 0.19443875 Lincoln Continental 0.16042361 Chrysler Imperial 0.12447530 Fiat 128 0.08346304 Honda Civic 0.09493784 Toyota Corolla 0.08732818 Toyota Corona 0.05697867 Dodge Challenger 0.06954069 AMC Javelin 0.05767659 Camaro Z28 0.10011654 Pontiac Firebird 0.12979822 Fiat X1-9 0.08334018 Porsche 914-2 0.05785170 Lotus Europa 0.08193899 Ford Pantera L 0.13831817 Ferrari Dino 0.12608583 Maserati Bora 0.49663919 Volvo 142E 0.05848459
通常、レバレッジ値が 2 より大きい観測値を詳しく調べます。
これを行う簡単な方法は、観測値をレバレッジ値に基づいて降順に並べ替えることです。
#sort observations by leverage, descending hats[ order (-hats[' hatvalues(model) ']), ] [1] 0.49663919 0.19443875 0.16042361 0.13831817 0.12979822 0.12608583 [7] 0.12447530 0.10011654 0.09828955 0.09493784 0.08816960 0.08732818 [13] 0.08346304 0.08334018 0.08193899 0.08097817 0.07614472 0.06954069 [19] 0.06287776 0.05945972 0.05848459 0.05785170 0.05767659 0.05697867 [25] 0.05102253 0.04235795 0.04235795 0.03990060 0.03990060 0.03890159 [31] 0.03890159 0.03890159
最高のレバレッジ値は0.4966であることがわかります。この数値は 2 を超えないため、データセット内のどの観測値も高い影響力を持っていないことがわかります。
ステップ 3: 各観測値の影響を視覚化する
最後に、各観測値の影響を視覚化するための簡単なチャートを作成できます。
#plot leverage values for each observation plot(hatvalues(model), type = ' h ')
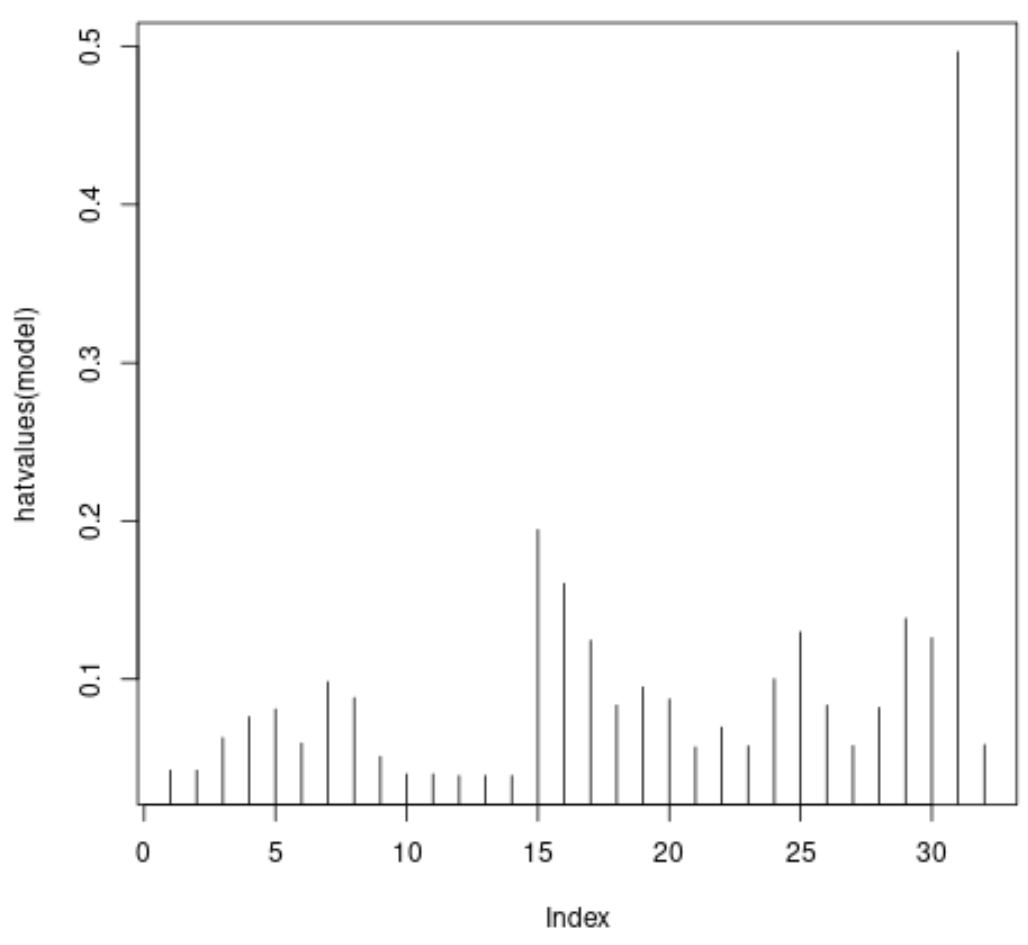
X 軸はデータセット内の各観測値のインデックスを表示し、Y 値は各観測値に対応するてこ比統計を表示します。
追加リソース
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る