Sas で対応のあるサンプルの t 検定を実行する方法
対のあるサンプルの t 検定は、一方のサンプルの各観測値がもう一方のサンプルの観測値と関連付けられる場合に、2 つのサンプルの平均を比較するために使用されます。
このチュートリアルでは、SAS で対応のあるサンプルの t 検定を実行する方法について説明します。
例: SAS での対応のあるサンプルの t 検定
教授が、特定のカリキュラムがテストの得点に影響するかどうかを判断したいとします。これをテストするために、彼は 15 人の学生をランダムに選択して事前テストを受けさせます。次に、各生徒にそのカリキュラムを 1 か月間受講させ、その後、同様の難易度の事後テストを受けさせます。
15 人の生徒それぞれのテスト結果は次のとおりです。
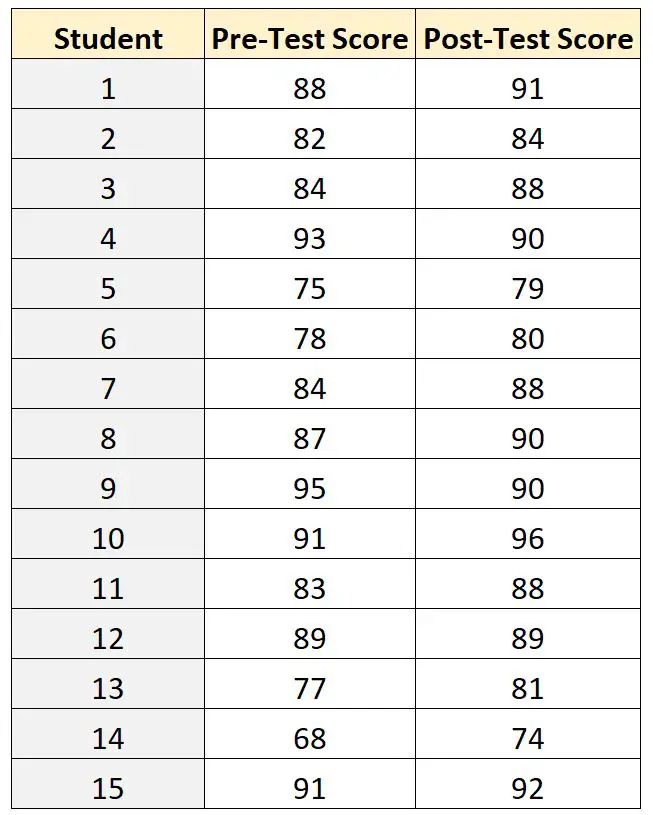
各生徒のテスト前のスコアをテスト後のスコアと関連付けることができるため、教師はテスト前とテスト後の平均スコアの差を比較するために、一対の t テスト サンプルを使用できます。
SAS でこの対応のあるサンプルの t 検定を実行するには、次の手順に従います。
ステップ 1: データを作成する
まず、次のコードを使用して SAS でデータセットを作成しましょう。
/*create dataset*/ datatest_scores ; input pre post; datalines ; 88 91 82 84 84 88 93 90 75 79 78 80 84 88 87 90 95 90 91 96 83 88 89 89 77 81 68 74 91 92 ; run ; /*view dataset*/ proc print data =test_scores;
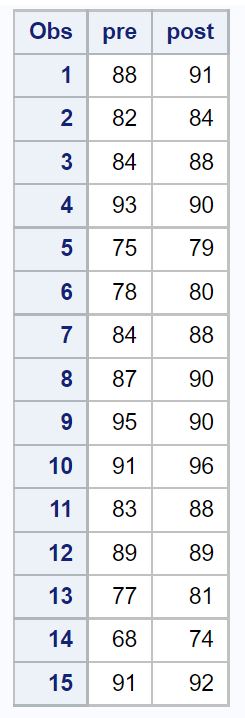
ステップ 2: 対応のあるサンプルの t 検定を実行する
次に、 proc ttestを使用して、対応のあるサンプルの t 検定を実行できます。
/*perform paired samples t-test*/
proc ttest data =test_scores alpha = .05 ;
paired pre*post;
run ;
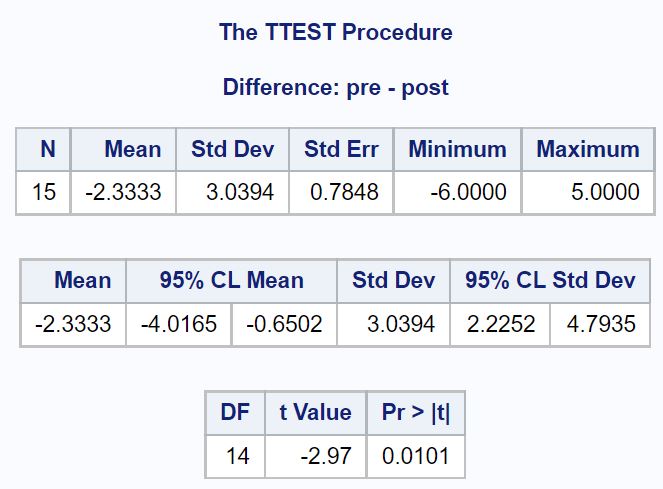
結果から次のことがわかります。
- テスト前とテスト後のスコア間の平均差: -2.3333
- 平均差の 95% 信頼区間: [-4.0165, -0.6502]
t 検定統計量と対応する両側 p 値も確認できます。
- t 検定統計量: -2.97
- p値: 0.0101
この例では、対応のあるサンプルの t 検定で次の帰無仮説と対立仮説が使用されます。
- H 0 :テスト前とテスト後の平均スコアが等しい
- H A :テスト前とテスト後の平均スコアは等しくない
p 値 ( 0.0101 ) は 0.05 未満であるため、帰無仮説を棄却します。
これは、学習プログラムに参加する前と後では、生徒のテストの真の平均点が異なると言える十分な証拠があることを意味します。
追加リソース
次のチュートリアルでは、SAS で他の一般的な統計テストを実行する方法について説明します。
SAS で 1 サンプルの t 検定を実行する方法
SAS で 2 サンプルの t 検定を実行する方法
SAS で Wilcoxon 署名付き順位テストを実行する方法