Sas で aic を計算する方法 (例あり)
赤池情報量基準 (AIC) は、重回帰モデルの適合度を比較するために使用される指標です。
次のように計算されます。
AIC = 2K – 2 ln (長さ)
金:
- K:モデルパラメータの数。 K のデフォルト値は 2 であるため、予測変数が 1 つだけあるモデルの K 値は 2+1 = 3 になります。
- ln (L) : モデルの対数尤度。ほとんどの統計ソフトウェアは、この値を自動的に計算できます。
AIC は、過剰な数のパラメーターを使用するモデルにペナルティを課しながら、データの変動を最も多く説明するモデルを見つけるように設計されています。
複数の回帰モデルを適合させたら、各モデルの AIC 値を比較できます。 AIC が低いほど、モデルはより適切になります。
次の例は、SAS のさまざまな回帰モデルの AIC を計算する方法を示しています。
例: SAS で AIC を計算する方法
3 つの異なる重線形回帰モデルを当てはめて、生徒がクラス内で達成する試験の成績を予測したいとします。
各モデルで使用する予測変数は次のとおりです。
- モデル 1 の予測変数: 学習に費やした時間
- モデル 2 の予測変数: 過去の実技試験
- モデル 3 の予測変数: 勉強に費やした時間と模擬試験の受験時間
まず、次のコードを使用して、20 人の生徒の情報を含むデータセットを作成します。
/*create dataset*/ data exam_data; input hours prep_exams score; datalines ; 1 1 76 2 3 78 2 3 85 4 5 88 2 2 72 1 2 69 5 1 94 4 1 94 2 0 88 4 3 92 4 4 90 3 3 75 6 2 96 5 4 90 3 4 82 4 4 85 6 5 99 2 1 83 1 0 62 2 1 76 ; run ;
次に、 proc regを使用してこれらの各回帰モデルを適合させ、 selection=adjrsq sse aicステートメントを使用して各モデルの AIC 値を計算します。
/*fit multiple linear regression models and calculate AIC for each model*/ proc reg data =exam_data; model score = hours prep_exams / selection=adjrsq sse aic; run ;
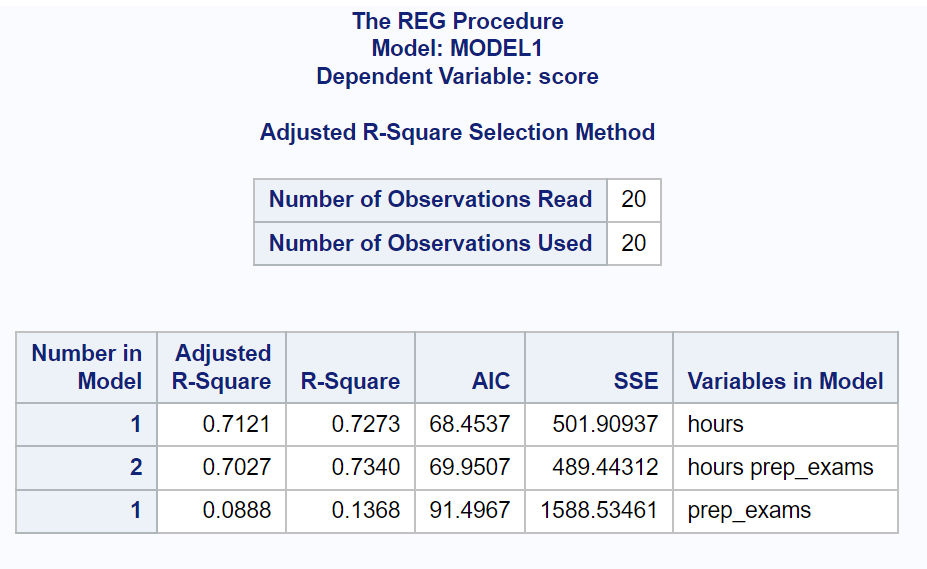
結果から、各モデルの AIC 値がわかります。
- 予測変数として時間を使用した AIC: 68.4537
- 時間数と試験を予測変数とした AIC: 69.9507
- 検査を予測変数とした AIC: 91.4967
AIC 値が最も低いモデルは、予測変数として時間のみを含むモデルです。
したがって、次のモデルがデータに最もよく適合すると宣言します。
スコア = β 0 + β 1 (学習時間)
このモデルが最適であると特定したら、それを当てはめて、R 二乗値やベータ係数を含む結果を分析して、学習時間と生徒の成績との正確な関係を判断できます。 ‘期末試験。
追加リソース
次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。
SAS で単純な線形回帰を実行する方法
SAS で重回帰を実行する方法
SAS で R 二乗を計算する方法
SAS で RMSE を計算する方法