Sas で多項式回帰を実行する方法
最も一般的なタイプの回帰分析は単純線形回帰で、予測変数と応答変数が線形関係にある場合に使用されます。
ただし、予測変数と応答変数の間の関係が非線形になる場合があります。
このような場合、変数間の非線形関係を説明できる多項式回帰を使用することが合理的です。
次の例は、SAS で多項式回帰を実行する方法を示しています。
例: SAS での多項式回帰
SAS に次のデータセットがあると仮定します。
/*create dataset*/ data my_data; input xy; datalines ; 2 18 4 14 4 16 5 17 6 18 7 23 7 25 8 28 9 32 12 29 ; run ; /*view dataset*/ proc print data =my_data;
ここで、データセット内の変数 x と y の間の関係を視覚化する散布図を作成するとします。
/*create scatter plot of x vs. y*/
proc sgplot data =my_data;
scatter x =x y =y;
run ;
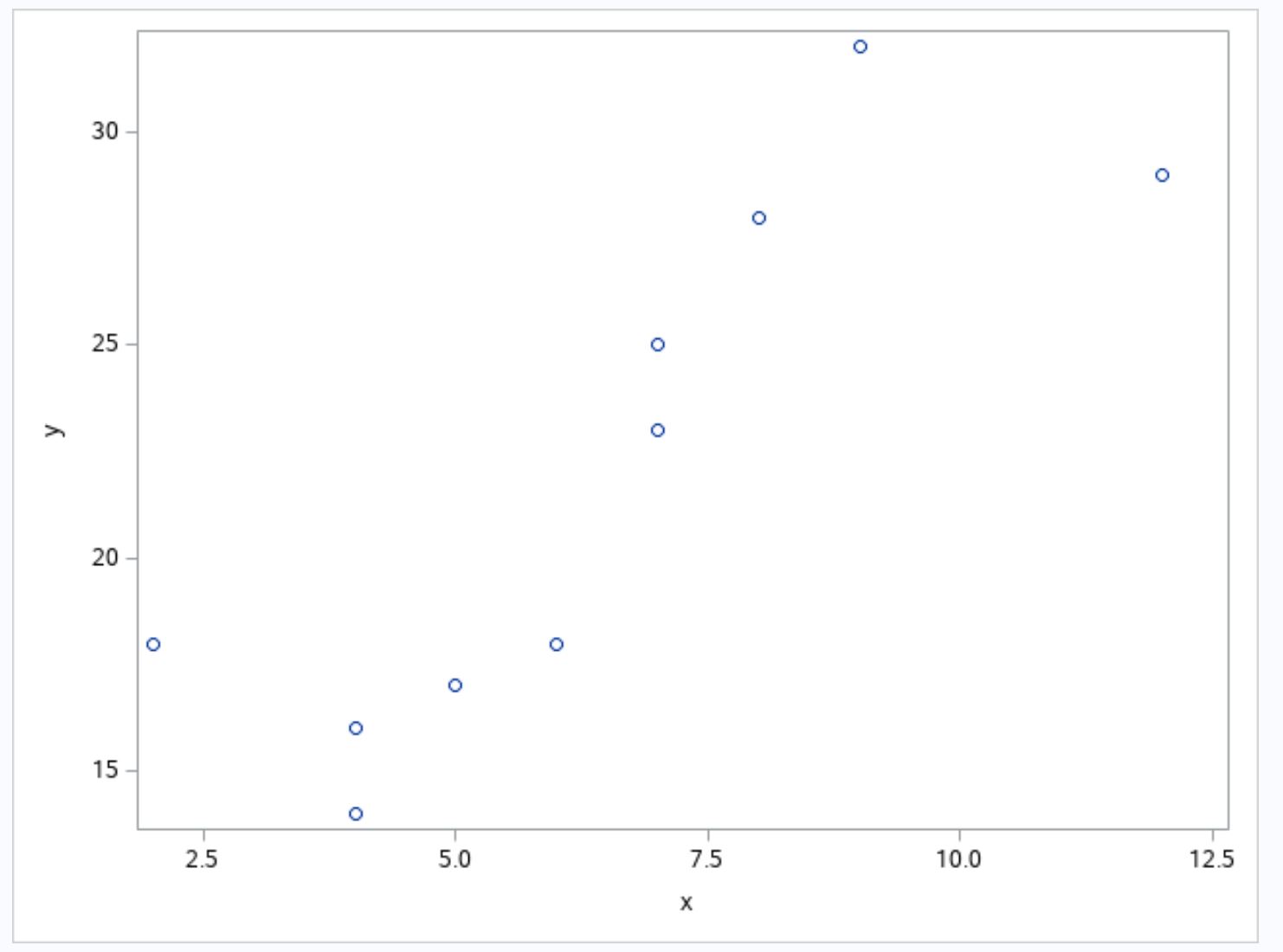
グラフから、x と y の関係が 3 次であることがわかります。
したがって、データセットに 2 つの新しい予測子変数 (x 2と x 3 ) を定義し、 proc regを使用して、これらの予測子変数を使用して多項式回帰モデルを近似します。
/*create dataset with new predictor variables*/ data my_data; input xy; x2 = x** 2 ; x3 = x** 3 ; datalines ; 2 18 4 14 4 16 5 17 6 18 7 23 7 25 8 28 9 32 12 29 ; run ; /*fit polynomial regression model*/ proc reg data =my_data; model y = x x2 x3; run ;
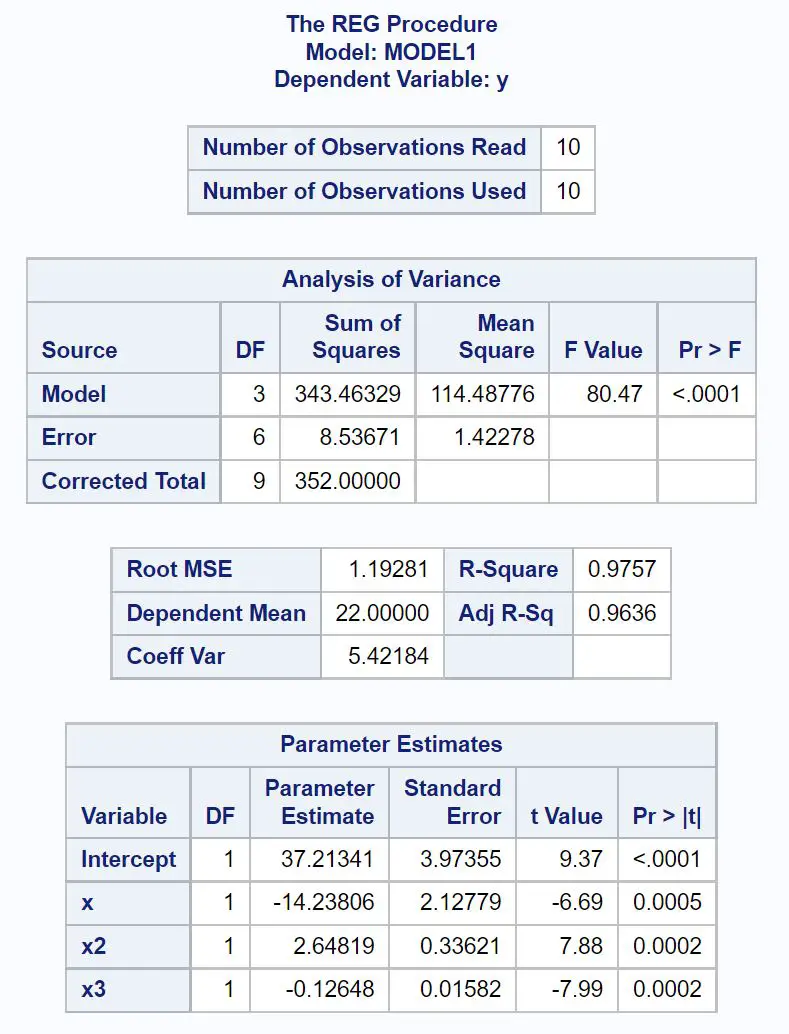
パラメーター推定値テーブルから係数推定値を見つけて、近似された多項式回帰方程式を次のように書くことができます。
y = 37.213 – 14.238x + 2.648x 2 – 0.126x 3
この方程式を使用すると、予測変数の指定された値から応答変数の期待値を求めることができます。
たとえば、xa の値が 4 の場合、y の値は 14.565 である必要があります。
y = 37.213 – 14.238(4) + 2.648(4) 2 – 0.126(4) 3 = 14.565
また、多項式回帰モデルの調整済み R 二乗値が0.9636であることもわかります。これは 1 に非常に近く、モデルがデータセットにうまく適合していることがわかります。
追加リソース
次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。