Sas で重回帰を実行する方法
重線形回帰は、 2 つ以上の予測変数と応答変数の間の関係を理解するために使用できる方法です。
このチュートリアルでは、SAS で多重線形回帰を実行する方法について説明します。
ステップ 1: データを作成する
学生の最終試験の成績を予測するために、学習に費やした時間数と受験した模擬試験の数を使用する重線形回帰モデルを当てはめるとします。
試験のスコア = β 0 + β 1 (時間) + β 2 (予備試験)
まず、次のコードを使用して、20 人の生徒の情報を含むデータセットを作成します。
/*create dataset*/ data exam_data; input hours prep_exams score; datalines ; 1 1 76 2 3 78 2 3 85 4 5 88 2 2 72 1 2 69 5 1 94 4 1 94 2 0 88 4 3 92 4 4 90 3 3 75 6 2 96 5 4 90 3 4 82 4 4 85 6 5 99 2 1 83 1 0 62 2 1 76 ; run ;
ステップ 2: 重回帰を実行する
次に、 proc reg を使用して重線形回帰モデルをデータに適合させます。
/*fit multiple linear regression model*/ proc reg data =exam_data; model score = hours prep_exams; run ;
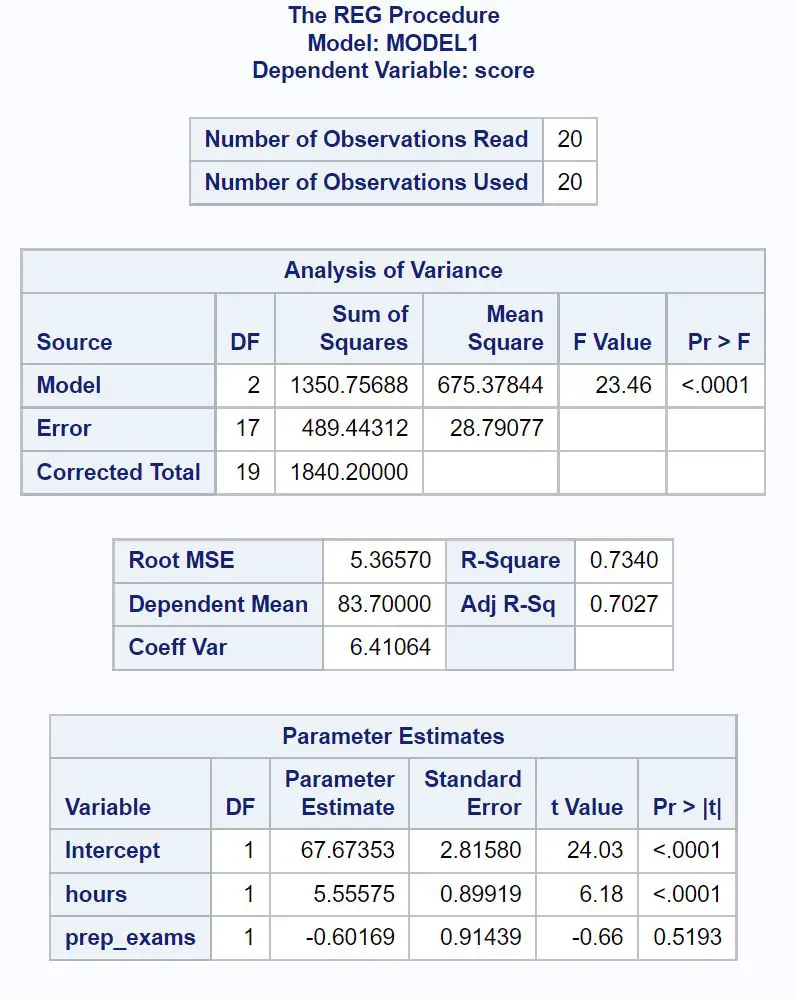
各表で最も関連性の高い数値を解釈する方法は次のとおりです。
ギャップ分析テーブル:
回帰モデルの全体的なF 値は23.46で、対応する p 値は<0.0001です。
この p 値は 0.05 未満であるため、回帰モデル全体が統計的に有意であると結論付けられます。
モデル適合表:
R 二乗値は、勉強時間数と受けた予備試験の数によって説明できる試験得点の変動のパーセンテージを示します。
一般に、回帰モデルのR 二乗値が大きいほど、予測変数は応答変数の値をより適切に予測します。
この場合、試験得点の変動の73.4%は、勉強時間数と受験した予備試験の数によって説明できます。
ルート MSE値も知っておくと役に立ちます。これは、観測値と回帰直線の間の平均距離を表します。
この回帰モデルでは、観測値は回帰直線から平均して5.3657単位逸脱します。
パラメータ推定値の表:
この表のパラメーター推定値を使用して、近似回帰式を書くことができます。
試験スコア = 67.674 + 5.556*(時間) – 0.602*(prep_exams)
この式を使用して、学習時間数と受験した模擬試験の数に基づいて、生徒の推定試験スコアを求めることができます。
たとえば、3 時間勉強して 2 つの予備試験を受けた学生は、試験スコア83.1を取得する必要があります。
試験の推定スコア = 67.674 + 5.556*(3) – 0.602*(2) = 83.1
時間の p 値 (<0.0001) は 0.05 未満であり、検査結果と統計的に有意な関連があることを意味します。
ただし、予備試験の p 値 (0.5193) は 0.05 未満ではありません。これは、試験結果と統計的に有意な関連性がないことを意味します。
予備試験は統計的に有意ではないため、モデルから削除し、代わりに調査時間を唯一の予測変数として使用して単純な線形回帰を実行することを決定する場合があります。
追加リソース
次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。