Sas で分位点回帰を実行する方法
線形回帰は、1 つ以上の予測変数と応答変数の間の関係を理解するために使用できる方法です。
通常、線形回帰を実行するときは、応答変数の平均値を推定する必要があります。
ただし、代わりに分位点回帰として知られる方法を使用して、応答値の任意のパーセンタイル値 (30 パーセンタイル、90 パーセンタイル、98 パーセンタイルなど) を推定することもできます。
SAS で分位回帰を実行するには、 proc quantregステートメントを使用できます。
次の例は、実際に SAS で分位点回帰を実行する方法を示しています。
例: SAS での分位点回帰の実行
SAS に、クラス内の生徒の学習時間数と対応する試験のスコアを示す次のデータセットがあるとします。
/*create dataset*/
data original_data;
input hours score;
datalines ;
1 75
1 79
2 78
2 83
2 85
3 84
3 84
3 89
4 93
4 88
4 79
4 94
5 96
5 98
;
run ;
/*view dataset*/
proc print data = original_data;
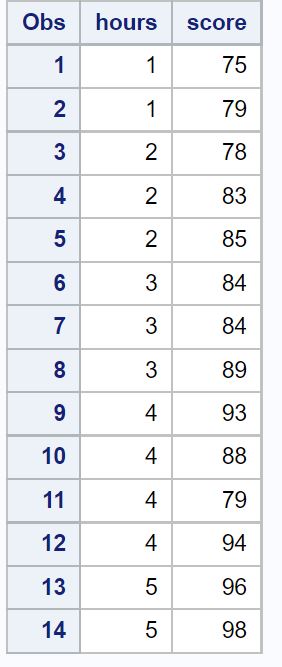
次に、学習時間を予測変数として、試験のスコアを応答変数として使用して、分位点回帰モデルを近似します。
このモデルを使用して、学習時間数に基づいて試験スコアの予想される 90 パーセンタイルを予測します。
/*perform quantile regression*/ proc quantreg data =original_data; model score = hours / quantile = 0.9 ; run ;
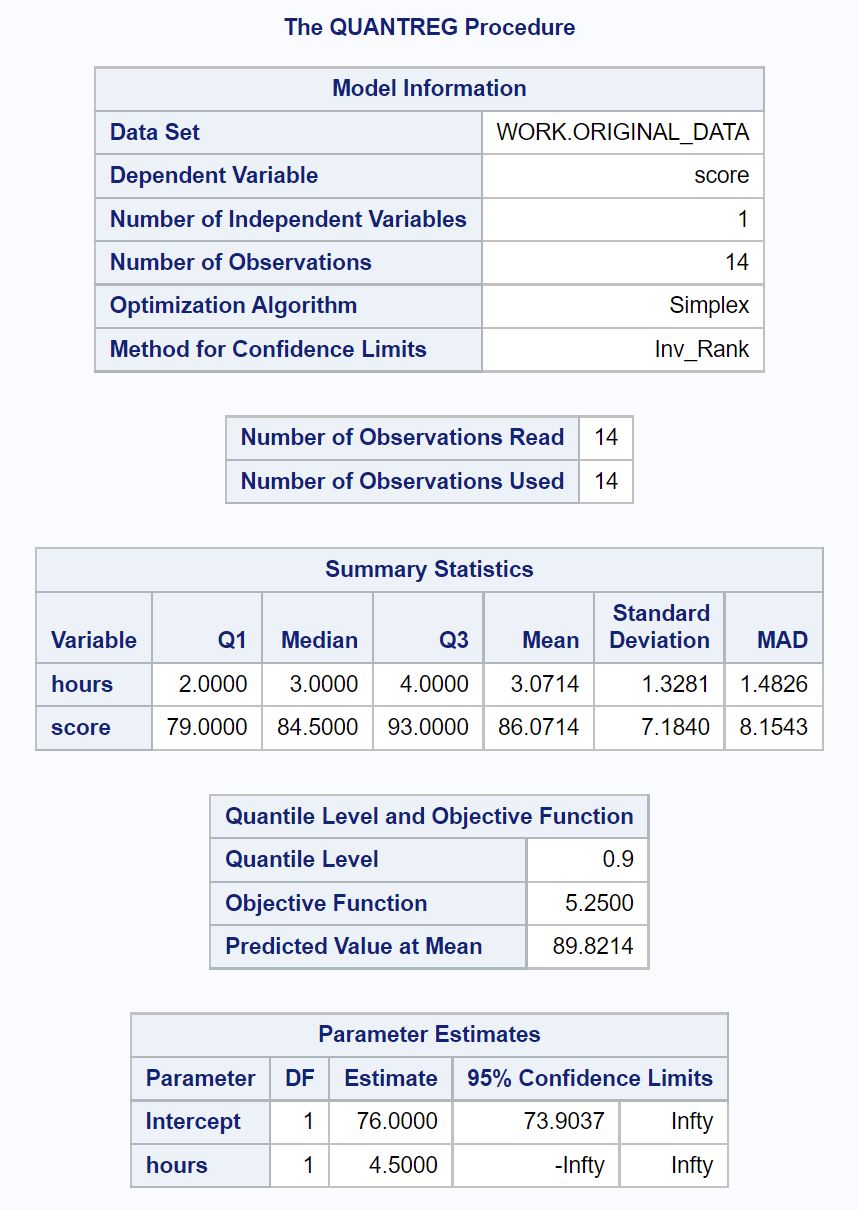
結果から、推定された回帰式がわかります。
90 パーセンタイルの試験スコア = 76 + 4.5 (時間)
たとえば、2 時間勉強した生徒全員の 90 パーセンタイル スコアは 85 になるはずです。
試験スコアの 90 パーセンタイル = 76 + 4.5*(2) = 85 。
出力には、プロット上に重ねて近似された回帰直線を含む生データの散布図も表示されます。
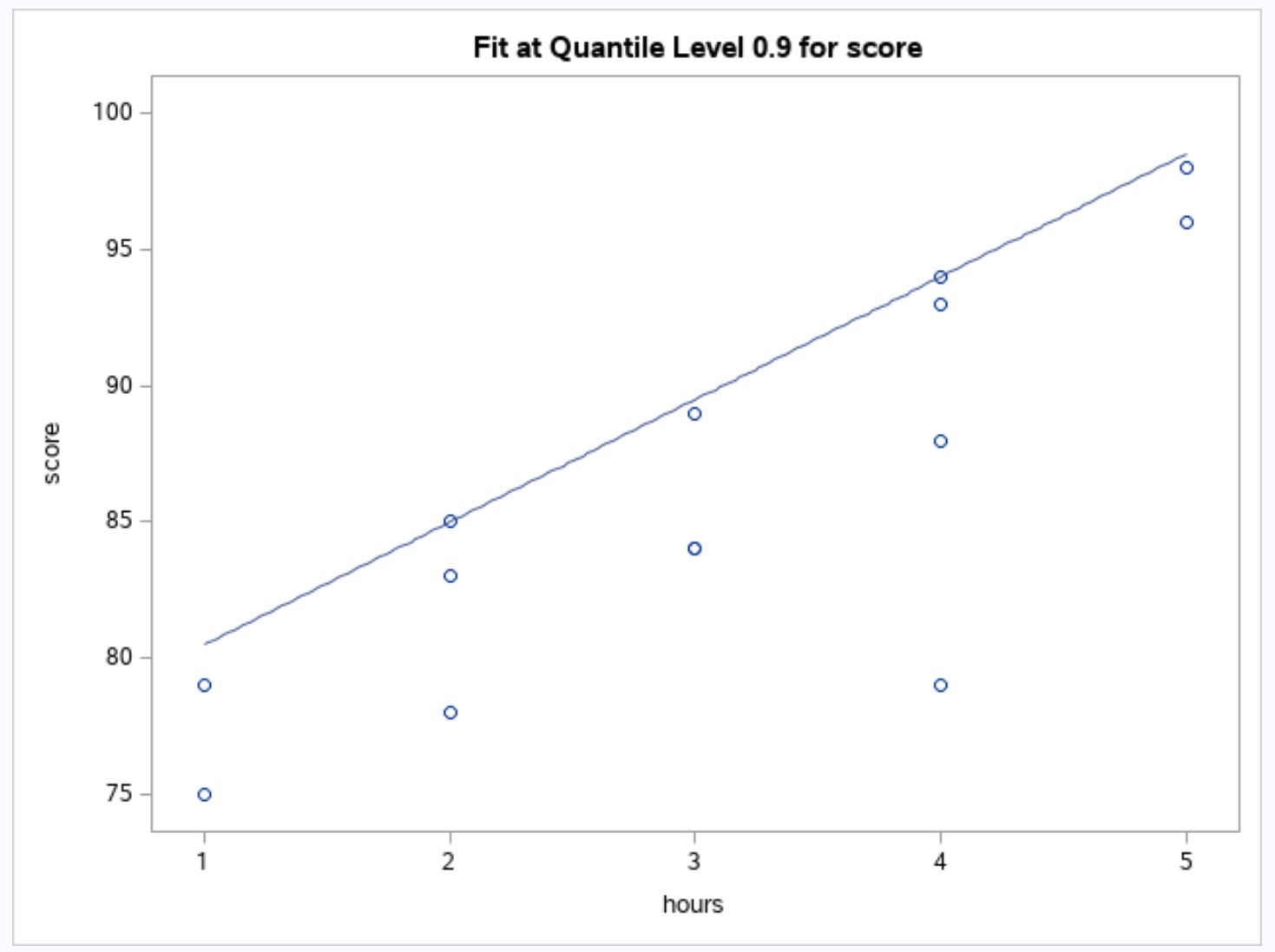
従来の回帰モデルとは異なり、この回帰モデルの近似線は、平均値ではなく、予測変数の各値の 90 パーセンタイルを通過します。
追加リソース
次のチュートリアルでは、R で他の一般的なタスクを実行する方法について説明します。