Sas で主成分分析を実行する方法
主成分分析 (PCA) は、データセット内の変動の大部分を説明する主成分 (予測変数の線形結合) を見つけようとする教師なし機械学習手法です。
SAS で PCA を実行する最も簡単な方法は、次の基本構文を使用するPROC PRINCOMPステートメントを使用することです。
proc princomp data =my_data out =out_data outstat =stats; var var1 var2 var3; run ;
各命令の動作は次のとおりです。
- data : PCA に使用するデータセットの名前
- out : すべての元のデータと主成分スコアを含む、作成するデータセットの名前
- outstat : 平均、標準偏差、相関係数、固有値、固有ベクトルを含むデータセットを作成することを指定します。
- var : 入力データセットから PCA に使用する変数。
次のステップバイステップの例は、実際にPROC PRINCOMPステートメントを使用して SAS で主成分分析を実行する方法を示しています。
ステップ 1: データセットを作成する
20 人のバスケットボール選手に関するさまざまな情報を含む次のデータセットがあるとします。
/*create dataset*/ data my_data; input points assists rebounds; datalines ; 22 8 4 29 7 3 10 4 12 5 5 15 35 6 2 8 3 10 10 4 8 8 4 3 2 5 17 4 5 19 9 9 4 7 6 4 31 5 3 4 6 13 5 7 8 8 8 4 10 4 8 20 4 6 25 8 8 18 8 3 ; run ; /*view dataset*/ proc print data =my_data;
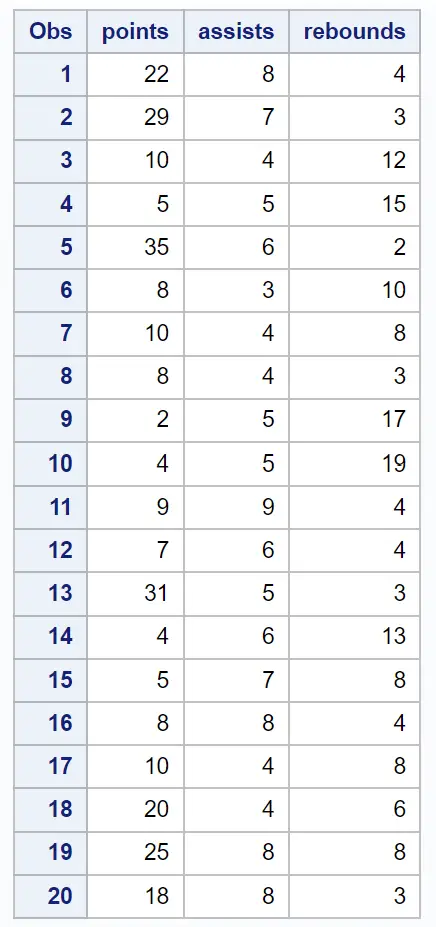
ステップ 2: 主成分分析を実行する
PROC PRINCOMPステートメントを使用すると、データセットのPoints 、 helps 、およびbounces変数を使用して主成分分析を実行できます。
/*perform principal components analysis*/ proc princomp data =my_data out =out_data outstat =stats; var points assists rebounds; run ;
出力の最初の部分には、各入力変数の平均値と標準偏差、相関行列、固有値と固有ベクトルの値を含むさまざまな記述統計が表示されます。
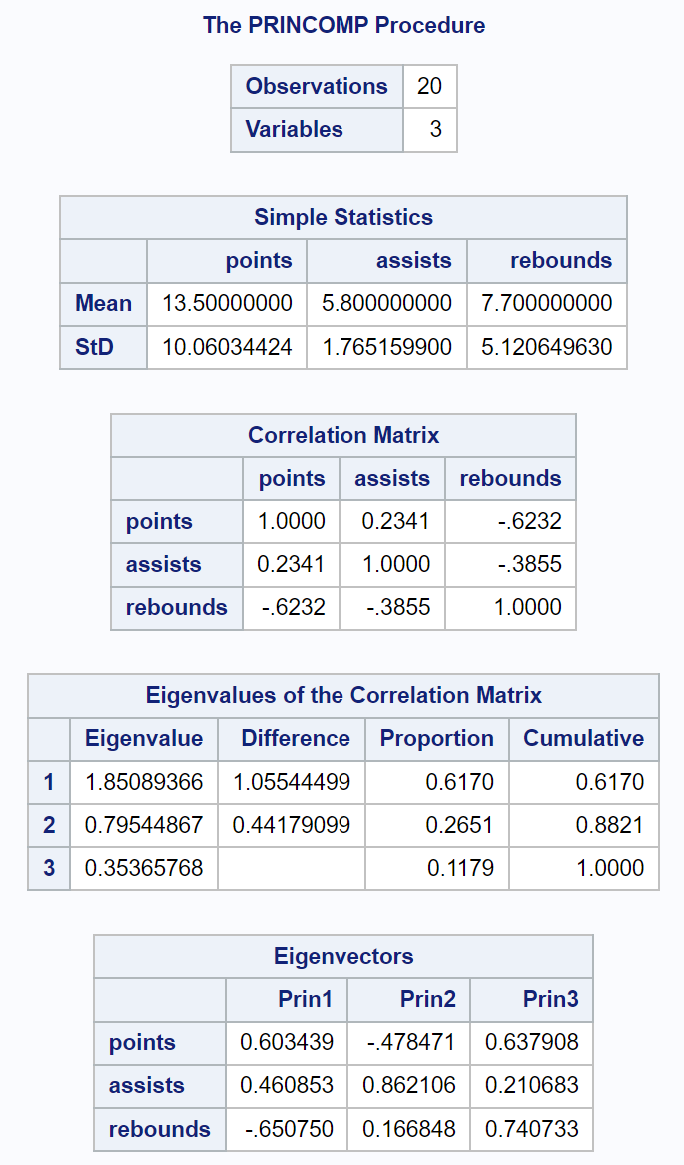
出力の次の部分には、スクリー プロットと説明された分散プロットが表示されます。
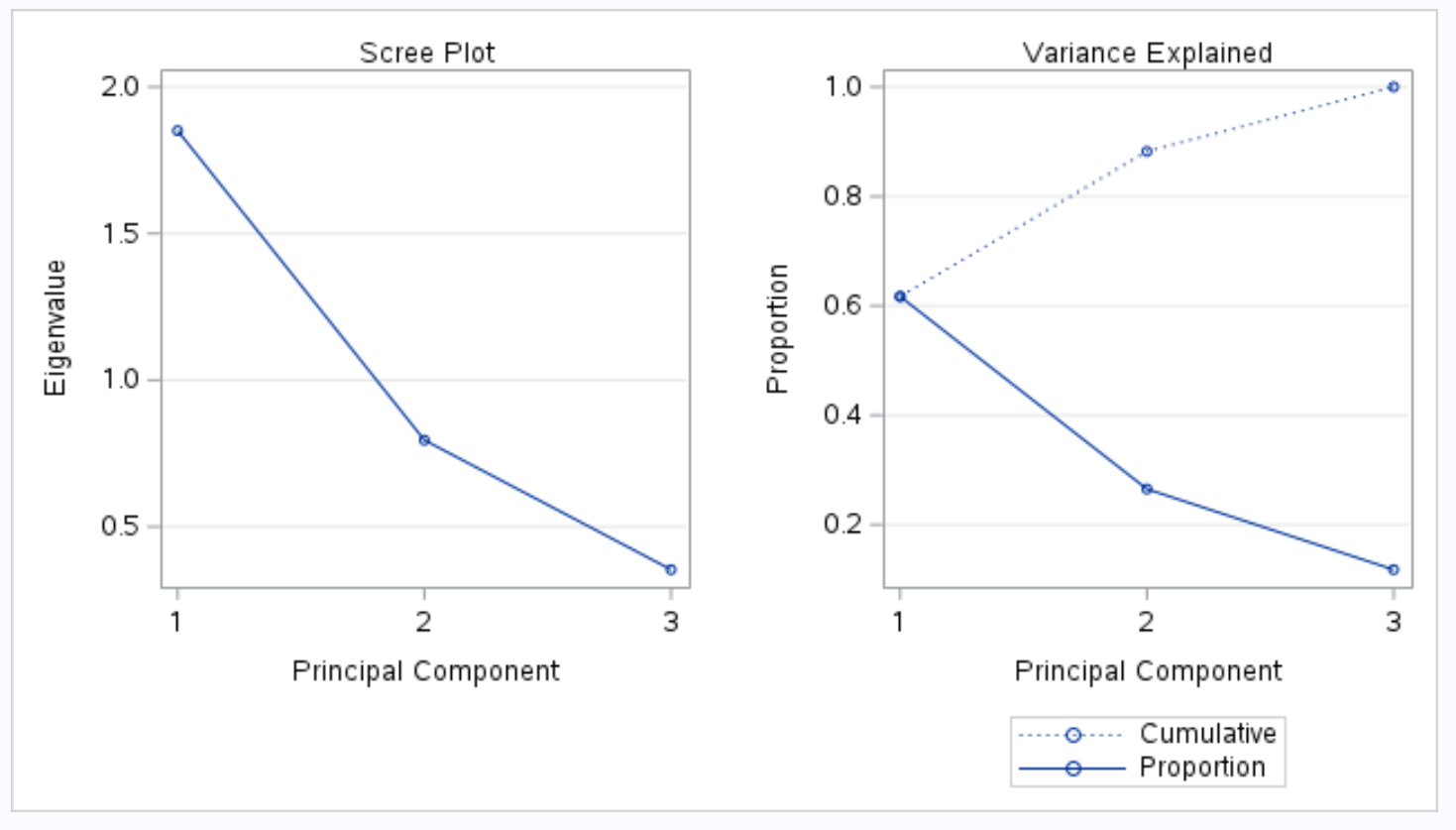
PCA を実行するとき、多くの場合、データセット内の変動全体の何パーセントが各主成分によって説明できるかを理解したいと考えます。
結果として得られる「相関行列固有値」という表では、変動全体の何パーセントが各主成分によって説明されているかを正確に確認できます。
- 第 1 主成分は、データセット内の変動全体の61.7%を説明します。
- 2 番目の主成分は、データセット内の変動全体の26.51%を説明します。
- 3 番目の主成分は、データセット内の変動全体の11.79%を説明します。
すべてのパーセンテージを合計すると 100% になることに注意してください。
「分散の説明」というタイトルのプロットを使用すると、これらの値を視覚化できます。
X 軸は主成分を表示し、Y 軸は個々の主成分によって説明される合計分散のパーセンテージを表示します。
ステップ 3: バイプロットを作成して結果を視覚化する
特定のデータセットの PCA の結果を視覚化するには、バイプロットを作成します。これは、データセット内の各観測値を最初の 2 つの主成分によって形成される平面上に表示するプロットです。
SAS では次の構文を使用してバイプロットを作成できます。
/*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
set out_data;
obs=_n_;
run ;
/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
scatter x =Prin1 y =Prin2 / datalabel =obs;
run ;
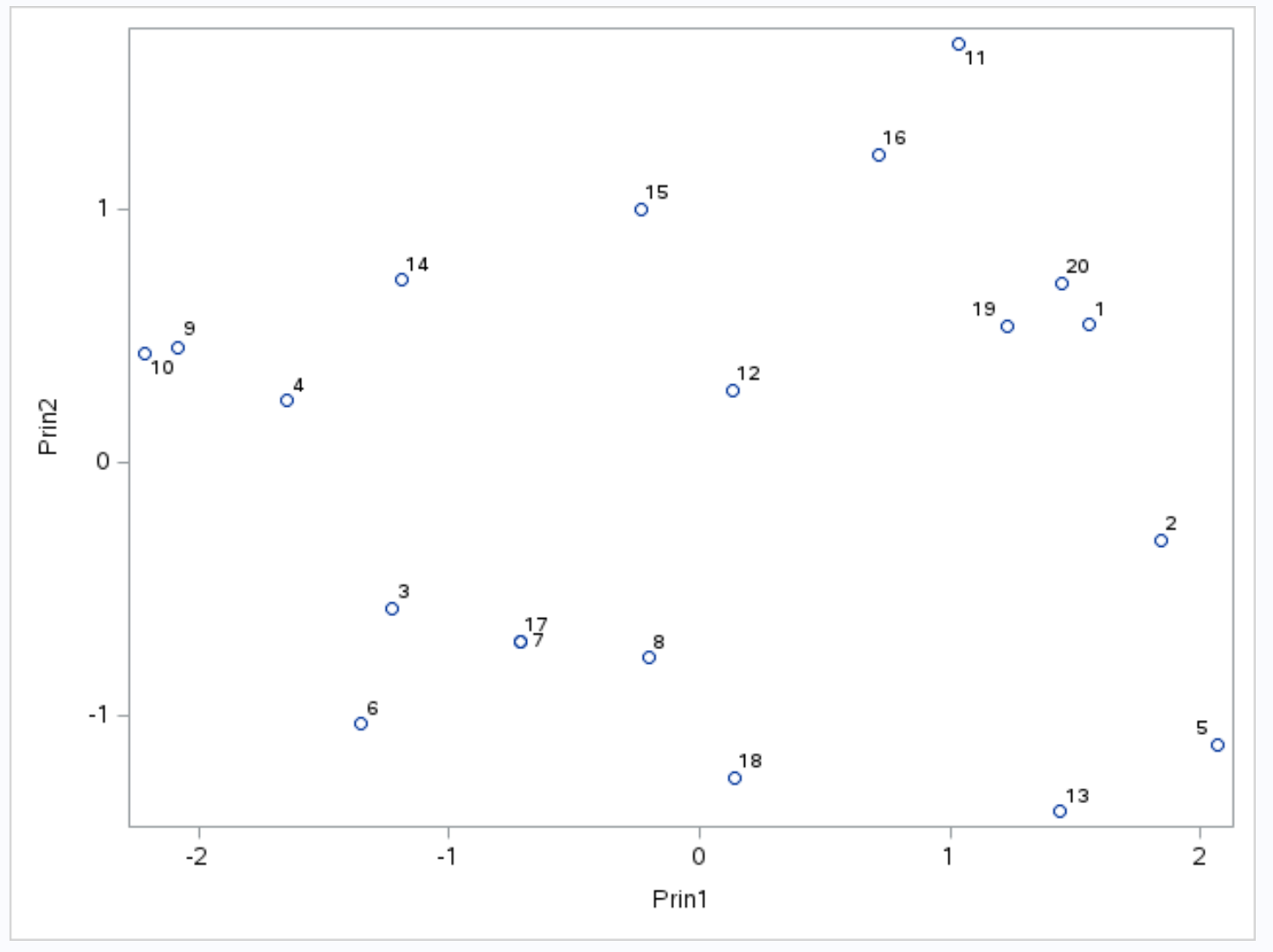
X 軸は第 1 主成分を表示し、Y 軸は第 2 主成分を表示します。データセットからの個々の観測値はグラフ内に小さな円として表示されます。
グラフ上に並んでいる観察結果は、ポイント、アシスト、リバウンドの 3 つの変数について同様の値を示しています。
たとえば、グラフの左端では、観測値#9と#10が互いに非常に近いことがわかります。
元のデータセットを参照すると、これらの観測値について次の値がわかります。
- 観察番号9 :2得点、5アシスト、17リバウンド
- 観察 #10 : 4 ポイント、5 アシスト、19 リバウンド
3 つの変数のそれぞれの値は類似しており、バイプロット上でこれらの観測値が互いに非常に近い理由が説明されています。
また、 「相関行列固有値」というタイトルの結果テーブルでは、最初の 2 つの主成分がデータセット内の変動全体の88.21%を占めていることもわかりました。
このパーセンテージは非常に高いため、バイプロット内のどの観測値が互いに近いかを分析することが有効です。これは、バイプロットを構成する 2 つの主成分がデータセット内の変動のほぼすべてを説明するためです。
追加リソース
次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。